裂纹叶片分布对失谐叶盘结构振动特性的影响

王艾伦，黄 飞

(1.中南大学 现代复杂装备设计与极端制造教育部重点实验室，长沙 410083;2.中南大学 机电工程学院，长沙 410083)

叶片—轮盘简称叶盘结构是叶轮机械的核心部件。理论上它是一种循环周期结构，实际上，由于不可避免的材料缺陷、制造误差以及使用磨损等因素，往往导致叶片的形状、刚度和质量等参数沿周向分布不完全相同，引起失谐。失谐可能造成叶盘结构出现振动局部化现象［1］。

由于叶盘结构工作条件恶劣，长期承受巨大的离心力和气流等静、动载荷作用，工作中的叶盘结构某些叶片将出现裂纹，并发现叶片上的裂纹多为穿透型裂纹［2－4］。显然，裂纹叶片是引发叶盘结构失谐的重要原因之一。许多学者对含有裂纹的单个叶片振动特性做了深入研究［5－6］，却很少有人对裂纹叶片引发的叶盘结构失谐进行研究。直到最近两年，国外才有相关论文发表。如Hou［7］通过分析在不同耦合条件下叶盘结构的固有频率变化和模态局部化，揭示了裂纹叶片引发叶盘结构失谐的机理，并探讨了含一个裂纹叶片的失谐叶盘结构振动特性;Fang［8］研究了含单个裂纹叶片的失谐叶盘结构的振动局部化问题，并探讨了裂纹深度、耦合度以及激励形式变化对失谐叶盘结构振动局部化程度的影响。然而，所作研究都针对含一个裂纹叶片的情况，且对裂纹叶片的处理均较粗糙。在工程实际中，裂纹往往同时出现在叶盘结构的好几个叶片上，前期研究已比较分析了含两个裂纹叶片与含一个裂纹叶片的失谐叶盘结构振动局部化问题，但是裂纹叶片的分布情况可能对失谐叶盘结构的振动特性有影响，而对这方面的研究至今还是空白。本文立足于工程实际问题，研究了两个裂纹叶片的分布对失谐叶盘结构振动特性的影响，为分析多个裂纹叶片的情况提供思路和方法。

1 含裂纹叶片的失谐叶盘结构有限元模型

对含裂纹叶片的失谐叶盘结构进行建模，最关键的是围绕裂纹前缘区域的模拟。由于裂纹尖端处的应力和应变是奇异的(裂纹前缘附近点的位移随r1/2的变化而变化，r是裂纹尖端到该点的距离)，三维裂纹模型的建立相当复杂。在实际处理过程中，人们通常采用弥散裂缝模型，即将裂纹模拟成一段横截面减小的狭槽。但是这种模型比较粗糙，受网格密度影响很大，对裂纹影响区域没有严格的定义。本文采用直接对含裂纹叶片的失谐叶盘进行局部处理及划分网格的实体建模方法［9］，建立了裂纹叶盘结构模型。这种方法精度高，适合用于创建任何带裂纹的复杂结构模型，而且还可以实现裂纹模型建立的程序化。

如图1所示有12个叶片的叶盘结构为钢质材料。叶片高120 mm，宽25 mm，厚8 mm;轮盘轴孔半径100 mm，外缘半径200 mm，厚24 mm。将整个结构划分为13个子结构，其中12个叶片子结构和1个轮盘子结构。

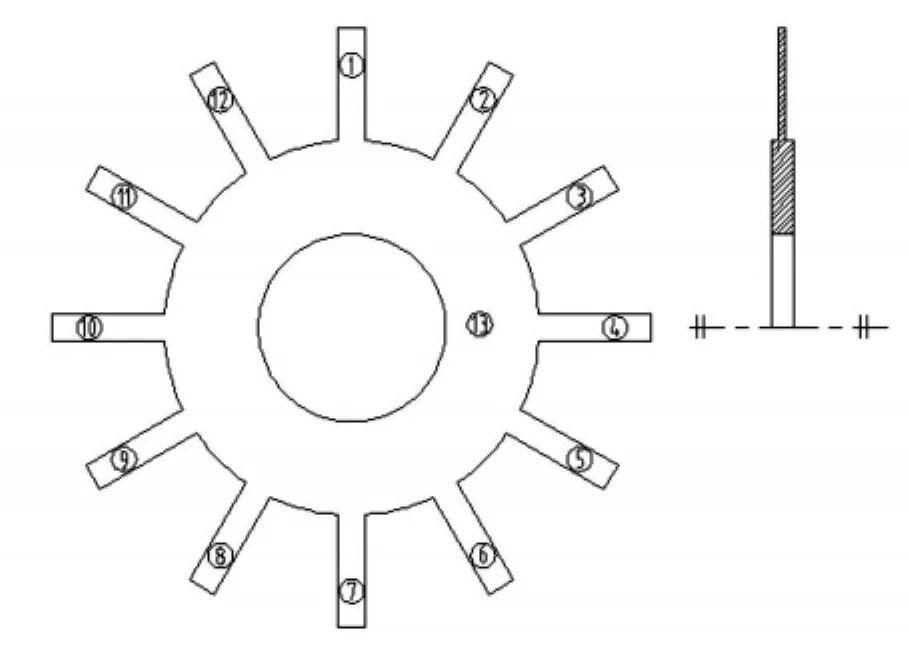
图1 谐调叶盘结构物理模型Fig.1 Physical model of bladed disk

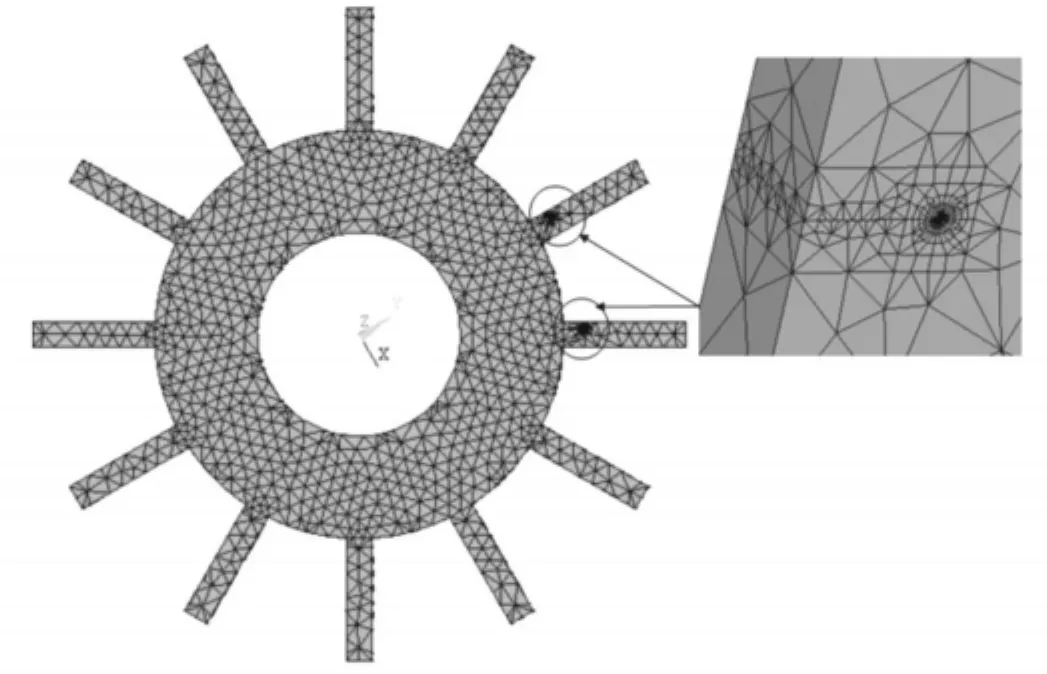
图2 含两个裂纹叶片的失谐叶盘结构有限元模型Fig.2 Finite element model of mistuned bladed disk with two cracked blades

为讨论问题的方便起见，现假定叶盘结构中仅有两个叶片上出现完全相同的穿透型裂纹，裂纹深度为8 mm，距轮盘轴心220 mm。采用实体建模方法建立含两个裂纹叶片的失谐叶盘结构模型，将包含裂纹部分的一小块体积从整个模型中分离出来并视为局部裂纹体，分别创建结构整体模型和局部裂纹体模型，然后再将两者合并。最终得到如图2所示的有限元模型，其中轮盘内孔所有节点的自由度全部约束。

2 裂纹叶片分布对失谐叶盘结构固有频率的影响

现对含两个裂纹叶片的失谐叶盘结构进行数值模拟。两个裂纹叶片的分布形式有多种情况，这里仅考虑两个裂纹叶片相邻(1、2号叶片上出现裂纹)、两个裂纹叶片相间(1、3号叶片上出现裂纹)、两个裂纹叶片相隔90度(1、4号叶片上出现裂纹)和两个裂纹叶片相隔180度(1、7号叶片上出现裂纹)的四种具有代表意义的分布情况。并定义叶盘结构的耦合强度为R=1－，其中:fb为单支叶片的基频;f0为叶盘耦合结构的基频［10］，子结构轮盘是决定叶片间耦合程度的主要因素。

图3为在两种典型耦合强度条件下，裂纹叶片的分布情况对旋转态和非旋转态下失谐叶盘结构固有频率的影响规律。

由图3可见，两个裂纹叶片的出现引起叶盘结构的基频降低，重固有频率对显著分离。当两个裂纹叶片处于相邻位置时，失谐叶盘结构的基频降低幅度最大，基频最小，而当两个裂纹叶片相隔180度时，失谐叶盘结构的基频降低幅度最小，基频最大。在弱耦合条件下，该现象更加明显，因此，裂纹叶片的分布情况对失谐叶盘结构的基频有一定影响。另外，发现失谐叶盘结构的某些固有频率(3阶和12阶)对裂纹以及裂纹叶片的分布情况不敏感。通过分析比较失谐叶盘结构在旋转态和非旋转态下的固有频率，可以看出失谐叶盘结构的各阶动频高于相应的静频，主要原因是离心力使失谐结构的刚性增加从而影响其固有频率(应力刚化效应)。

3 裂纹叶片分布对失谐叶盘结构固有振型的影响

图4为在两种典型耦合强度条件下两个裂纹叶片的分布情况对失谐叶盘系统一阶固有振型的影响规律。

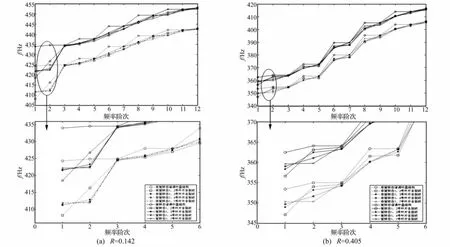
图3 裂纹叶片分布情况对失谐叶盘结构固有频率的影响规律Fig.3 Fundamental frequency variation of mistuned bladed disk with the Distribution of cracked blades

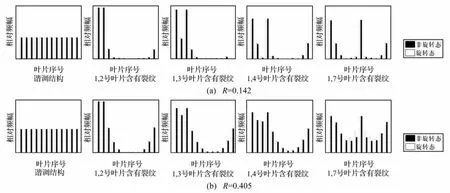
图4 裂纹叶片的分布情况对失谐叶盘结构固有振型的影响规律Fig.4 Mode variation of the mistuned bladed disk with the distribution of cracked blades

从图4可以看出，当两个裂纹叶片处于相邻位置时，失谐叶盘结构的模态局部化程度最高，而两个裂纹叶片相隔180°时，其模态局部化程度最低，且该现象在弱耦合条件下尤为突出，因此裂纹叶片的分布情况对失谐叶盘结构的模态局部化程度有较大影响。这是由于不同的裂纹叶片分布情况对谐调叶盘结构的循环对称性破坏程度不同导致的，当两个裂纹叶片呈相邻分布时，其对谐调叶盘结构的循环对称性破坏最严重，故该种情况下失谐叶盘结构的振动局部化程度最大。此外，通过比较失谐叶盘结构的旋转态和非旋转态下的一阶固有振型可以发现，离心力(转速)对含两个裂纹叶片的失谐叶盘结构振动局部化程度有减弱作用。

4 结论

(1)两个裂纹叶片的分布情况对失谐叶盘结构的基频有较大影响，当两个裂纹叶片处于相邻位置时，基频下降幅度最大，并发现失谐叶盘结构的某些固有频率对裂纹以及裂纹叶片的分布情况不敏感。

(2)失谐叶盘结构的振动局部化程度与谐调叶盘结构的循环对称性破坏程度有关。两个裂纹叶片的分布情况决定其对谐调叶盘结构的循环对称性破坏程度，当两个裂纹叶片相临分布时对谐调叶盘结构的循环对称性破坏最严重，故其振动局部化程度最高。

(3)失谐叶盘结构所处状态以及叶片间耦合程度对其振动局部化程度有影响。在强耦合条件下的旋转态失谐叶盘结构振动局部化程度较弱。

［1］Wei S T，Pierre C.Localization phenomena in mistuned assemblies with cyclic symmetry part 1:free vibrations［J］.ASME， JournalofVibration， Acoustics， Stress， and Reliability in Design，1988，110:429－438.

［2］Bernstein H L，Alien J M.Analysis of cracked gas turbine blades［J］.Journal of Engineering for Gas Turbines and Power，1992，114:293 －301.

［3］Walls D P，Delaneuville R E，Cunningham S E.Damage tolerance based life prediction In gas turbine engine blades under vibratory high cycle fatigue［J］.Journal of Engineering for Gas Turbines and Power，1997，119:143 －146.

［4］Hou J，Wicks B J，Antoniou R A.An investigation of fatigue failures of turbine blades in a gas turbine engine by mechanical analysis ［J］.Engineering Failure Analysis，2002，9:201－211.

［5］Wauer J.Dynamics of cracked rotating blades［J］.Applied Mechanics Reviews，1991，44:273 －278.

［6］Dimarogonas A D.Vibration of cracked structures:A state of artReview［J］.Engineering Fracture Mechanics，1996，55:831－857.

［7］Hou J F，Cracking induced mistuning in blade disks［J］.AIAA Journal，2006，44:2542 －2546.

［8］Fang X，Tang J.Crack induced vibration localization in simplified bladed-disk structures［J］.Journal of Sound and Vibration，2006，291:395－418.

［9］王 峰，黄其青，殷之平.三维裂纹应力强度因子计算［J］.航空计算技术，2006，36(3):125 －127.

［10］周传月，邹经湘.失调对叶片－轮盘耦合系统振动影响的预测［J］.航空学报，2001，22(5):211－214.