基于独立分量分析的管道异常振动事件定位方法

张景川，曾周末，曹庆松，封 皓，靳世久

(天津大学 精密测试技术与仪器国家重点实验室，天津 300072)

随着油气资源的开发以及能源需求的激增，管道运输作为一种安全、经济的运输方式在世界各地得到广泛应用。由于管道输送介质的危险性和污染性，管道泄漏会造成巨大的环境污染、经济损失及人身伤害，因此管道安全状态的实时检测技术已成为重要的研究课题［1-3］。本课题组针对造成管道泄漏的诸多因素，研发了基于Mach-Zehnder光纤干涉仪原理的分布式光纤油气管道安全监测系统。它能够对威胁管道安全的行为进行实时监测、预警以及定位，并已于2007年成功应用于大港-枣庄成品油管道［4-5］。在管道安全监测系统(以下简称系统)中，管道泄漏和非法入侵事件的模式识别以及事发点精确定位技术是系统中非常关键的技术，本文仅对管道沿线异常振动事件精确定位技术进行研究。如何在长距离、周围环境复杂(管道经过农田、河流、铁路等)、破坏因素多(蓄意入侵、机械施工等)的条件下精确而迅速地定位管道异常入侵事发点，是系统亟需解决的问题。

时间延迟估计(TDE)是管道定位检测中的一项关键技术，通过估计信号的时间延迟可以计算出入侵事发点的位置。时延估计的基本方法是互相关时延估计法。然而，现场环境中存在着不可预知、强度复杂的噪声，这些噪声严重影响了时间延迟估计的精度，降低了定位的精确性。为了提高时延估计的精度和抗干扰能力，目前所用的各种时延估计方法有:自适应时延估计、广义相位时延估计和LMS时延估计［6-8］等。这些方法虽然可以在一定程度上提高时延估计精度，但其实质仍是在传统互相关时延估计基础上改进，并要求观测噪声互不相关，对于相关高斯噪声干扰，其时延估计性能将急剧下降［9］。

独立分量分析(Independent Component Analysis，ICA)是近20年发展起来的一种信号处理和数据分析方法，在信号处理、数据挖掘、特征提取、神经网络等许多领域有广泛的应用。ICA具有“去冗余”的特点，并能抑制高斯噪声［10-11］。本文结合ICA的特点提出了基于独立分量分析的互相关时延估计算法用于定位管道异常入侵事发点，仿真结果和港枣线成品油管道的现场实验结果证明该方法可以有效地消除相关高斯噪声的影响，相比传统互相关时延估计法，可进一步降低时延估计的平均误差和均方差，提高定位精度和一致性。

1 系统定位方法

1.1 定位原理

本系统基于Mach-Zehnder光纤干涉仪原理，沿管道平行敷设一条光缆，利用其中的3条单模光纤构成分布式微振动传感器，实时获取管道沿线的振动信号。系统定位检测原理如图1所示。

图1 系统定位检测原理图Fig.1 The location principle of system

光缆中的两条光纤F1与F2构成传感臂，第3条光纤F3用于传输信号。光源发出的连续光波在耦合器1处分为光强为1∶1的两束光，在两条传感光纤中同时反向传播。当管道沿线发生威胁管道安全的异常事件时，光缆感受到土壤的振动，由于两条传感光纤在光缆中排列位置不同，会产生不同的应变。应变使光波产生相位调制，两束相干光的相位差随之发生改变，从而使干涉光强和转化电流发生改变。系统通过检测光电探测器输出电流的变化便可获取光缆沿线上的振动信号。由于两束干涉光波传播路径不同，因此两束干涉光波先后到达2个光电探测器会产生一个时间差，系统通过计算这个时间差，即可对入侵点精确定位。

根据上述定位原理的表述，设L为管道总长度;x为入侵点至管道首端的距离;光波在光纤中传播速度为v，其中v=c/n，c是光在真空中的速度3×108m/s;n是光纤的折射率;光波从入侵点沿方向1传播到首端的时间为t1;从入侵点沿方向2传播到首端的时间为t2;光波从入侵点沿方向1传播到首端的路径为s1;从入侵点沿方向2传播到首端的路径为s2;两方向上光波的路径差为Δs，相应的时间差为Δt，则可得上述变量之间的关系为:

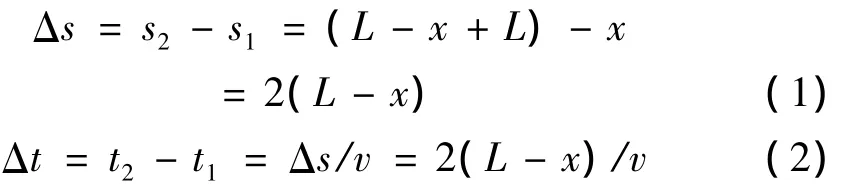
根据式(2)得定位公式:

由式(3)可知，若要精确定位事发点位置，必须精确获取两路干涉光信号到达光电探测器的时间差，即时间差的精度决定异常事件点的定位精度。

1.2 传统互相关法估计时间差

同一光源发出的两组光波同时在传感光纤F1与F2中反向传播，传播过程中叠加噪声。分布式光纤传感器两端的检测信号可分别表示为:

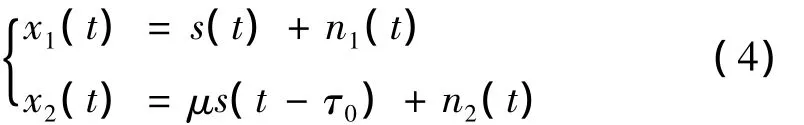
式(4)中:x1(t)和x2(t)分别为2个光电探测器检测到的信号;s(t)是管道沿线振动信号为零均值非高斯非平稳随机过程;n1(t)和n2(t)是加性噪声为零均值高斯平稳随机过程，且与振动信号相互独立;μ是衰减因子;τ0为信号的时延。

两个光电探测器分别检测到的光信号由于是同一个振动源作用在光纤而得，因此2路检测信号具有非常高的相关性，时延τ0可由其互相关函数计算得到。由式(4)可得两个信号的相关函数:

式(5)中:Rss(τ-τ0)为2路振动信号的自相关函数;Rsn1(τ-τ0)和Rsn2(τ)分别表示振动信号与噪声的互相关函数;Rn1n2(τ)为噪声之间的互相关函数，假定振动信号与噪声以及噪声与噪声之间互不相关，则式(5)变为:

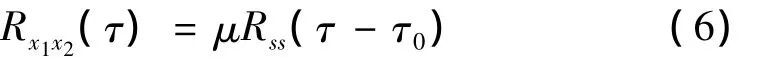
但实际上，高斯噪声存在相关性［12］，则式(6)变为:

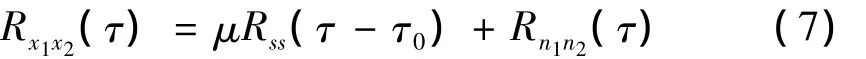
与式(6)相比，式(7)中增加了n1(t)和n2(t)的自相关函数Rn1n2(τ)。这时，Rx1x2(τ)不仅和2路振动信号的自相关函数 Rss(τ-τ0)有关，而且和 Rn1n2(τ)有关。在式(6)中，表示振动信号x1(t)和x2(t)时延的Rss(τ-τ0)的峰值出现在 τ=τ0，但在式(7)中，由于Rn1n2(τ)＞0，Rx1x2(τ)的最大值将偏离 τ0，从而产生时延估计误差，传统互相关法时延估计性能将严重下降。ICA技术可以分离出观测信号中的高斯噪声，因此，本文提出基于独立分量分析的互相关时延估计算法估计时延。

2 基于ICA的互相关定位法

2.1 ICA原理与算法

ICA通过分析多维观测数据间的高阶统计相关性，找出相互独立的隐含信息成分，完成分量间高阶冗余的去除及独立信源的提取。设X=(x1，x2，…，xm)T为m个传感器测得的m维信号，是由n个未知独立源信号S=(s1，s2，…，snm)T经过一个m×n维的混合矩阵A线型混合而成，满足:

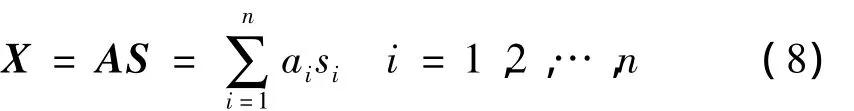
ICA就是在源信号S和混合矩阵A都未知的情况下，求解一个分离矩阵W，使得观测信号X通过它后所得输出Y是S的最优逼迫，即:

ICA原理主要是建立度量Y独立性的判据，并在此判据下利用各种优化方法寻找最优的分离矩阵W。不同的判别准则和优化方法对应着不同的ICA算法，本文采用的是基于负熵的快速定点迭代算法FastICA［13］。具体过程为:

(1)对原始检测信号做去均值和白化预处理，设白化后的信号为，则满足E()=I;

(2)任意选择具有单位方差的初始分离矩阵wi(0);

(5)判断wi(n+1)是否收敛，若收敛则分离出一个独立分量，否则返回步骤(3);

(6)判断混合信号中的多个独立分量是否已经全部分离完毕，若没有则返回(2)，否则分离过程结束。

2.2 基于ICA的互相关法估计时间差

在基本ICA模型中，观测信号通道数需大于等于独立信号源数。管道安全监测系统装有2个光电探测器，对振动信号同步采集，由于在现场信号采集过程中，各种噪声和干扰的来源是复杂多样的，难以精确区分，且大都是高斯白噪声，从信号出现的统计规律来说，可以将其归为“同源”，因此对这种包含高斯噪声的振动信号做独立分量分析更符合实际情况，这完全满足ICA对观测信号通道数的要求。振动信号可以看作一个非高斯过程，而噪声是高斯过程，两者是相互独立的，满足ICA技术的信号源彼此统计独立的前提要求。因此，本文对检测信号进行ICA分解，分离出高斯噪声，然后，每路信号减去高斯噪声，最后两路信号进行互相关估计时延。

根据上述时延估计原理的表述，分布式光纤传感器两端的检测信号经过FastICA处理后得到独立分量Y=WX=［y1，y2］，设 y2为分解出的高斯噪声分量，然后，每路信号减去高斯噪声则由式(4)可得:

由式(10)可得两个信号的相关函数:

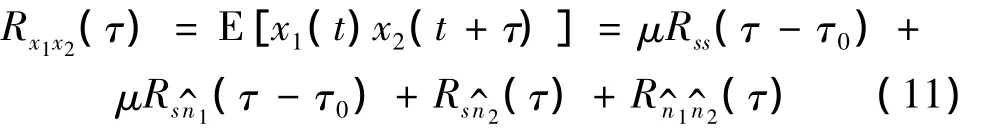
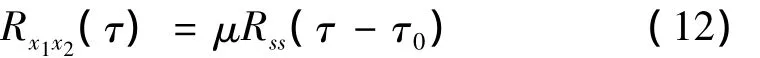
因此当式(12)中 τ=τ0时，Rx1x2(τ)取得最大值，极大得提高了系统对异常事件事发点的定位精度。

3 仿真结果

本文首先通过计算机仿真实验来验证本文方法的有效性。当噪声相关时，两路光电检测信号可假设为如下形式:

设式(13)中，D=5，真正的时延参数 τ0=10，并设s(t)=5cos［sin(10πt)+sin(5πt)］，n1(t)是零均值方差为1的高斯白噪声，数据长度为N=1000，信噪比为0 dB。

图2和图3分别显示了传统的互相关方法以及本文方法作10次Monte Carlo试验所估计出的时延图形。从图2中可以看出，传统的互相关方法在t=5和t=10处均有较明显的峰值，前者是由噪声之间的相关性所致，而后者则是信号之间的时延产生。由于难于将二者区分开来，因此传统互相关法无法给出正确的时延估计。相反的，图3表明，本文方法则能有效地估计出正确的时延参数τ0=10。

图2 传统互相关法估计时延Fig.2 Conventional cross-correlation algorithm for time delay estimation

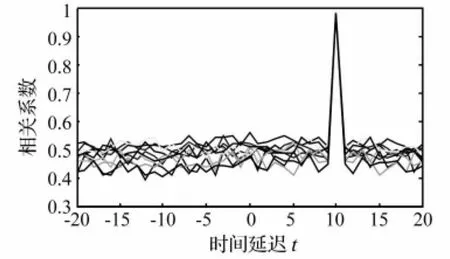
图3 基于ICA互相关法估计时延Fig.3 Cross-correlation algorithm for time delay estimation based on ICA

4 现场实验结果与分析

4.1 实验方案

系统为2007年在大港—枣庄成品油管道成功安装运行的分布式光纤管道安全监测系统，监测距离约35公里。系统采用的传感光缆为2006年建设该成品油管道时与管道同沟敷设的GYTA六芯单模通讯光缆，位于管道正上方约30 cm处，与地面垂直距离约1.5 m。光源采用半导体激光器(LD)，其波长为1550 nm，功率为22 mW。光电检测器采用InGaAs光电二极管，反应速度为0.1 ns。为了对管道沿线破坏性挖掘行为进行定位检测，在大港—枣庄成品油管道现场距首站34km处对光缆上方地表旁0.5 m处进行模拟人工挖掘实验。系统采用美国NI公司数据采集卡和Lab-VIEW软件对人工挖掘情况下管道沿线振动信号进行数据采集，采样频率为2.5 MHz，每组数据长1 s，共含有2500000个采样点。

4.2 定位结果

图4(a)、图4(b)为现场实验中测得的人工挖掘振动信号，图4(c)、图4(d)为利用FastICA算法进行独立分量分析后的结果。图4(c)即为ICA降噪后的振动波形，从图4(c)中可以看出振动信号被很好地分离了出来，且波动特征非常明显。ICA分离出的噪声符合高斯分布如图5所示，这也证明ICA可以很好地分离出信号中的高斯分量。对比图4(a)与图4(c)还可以看出，滤波后曲线的总体形态保持不变，虽然幅值单位发生了变化，但经过归一化后，并不影响相关定位计算。

图4 双通道振动信号曲线［(a)～(b)］以及独立分量分析结果［(c)～(d)］Fig.4 Vibration signals in two channels［(a)～(b)］and ICA results［(c)～(d)］

系统对距大港输油首站34km处人工铁锨挖掘情况下管道沿线振动信号采集了40组数据，利用本文方法进行了定位计算，40次定位结果分布情况如图6所示。表1表明了两种时延估计方法处理40组数据的比较结果，从表1中可以看出基于ICA的互相关法定位误差明显减小，这证明了本文方法比传统互相关法有明显的优势。

图5 噪声概率密度分布图Fig.5 Probability density distribution of noise

图6 基于ICA互相关法的34km处定位结果Fig.6 Cross-correlation algorithm for location results at the 34km based on ICA

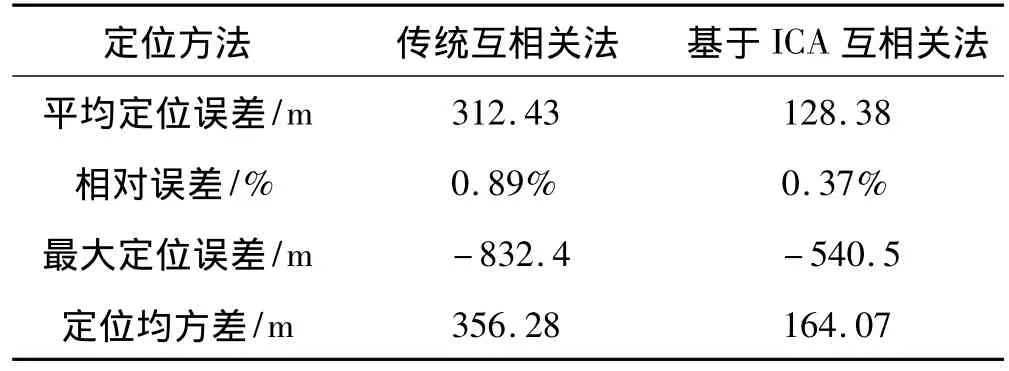
表1 定位结果比较Tab.1 Comparison of location results

5 结论

本文根据分布式光纤油气管道安全监测系统采集的振动信号，将独立分量分析方法应用于油气管道定位检测中，提出了基于独立分量分析的互相关时延估计方法用于管道异常振动事件定位。研究结果表明:ICA可以有效地分离出检测信号中的高斯分量;同时，两路检测信号分别减去ICA分离出的高斯分量后，信号中所蕴含的高斯噪声相关性严重下降，本文方法能有效抑制相关高斯噪声对时延估计的干扰;最后，经过大量实验证明，对于管道周围1.5 m范围内铁锨挖掘引起的微小振动，利用本文方法进行数据处理后的平均定位误差小于150 m，相对误差小于0.4%，最大定位误差不超过±600 m，定位均方差小于200 m，相比传统互相关时延估计法，本文方法适用于相关高斯噪声干扰情况下的准确时延估计，进一步提高了定位精度和一致性，可以实现管道安全状态的在线监测，因此具有很好应用前景。

［1］Lockwood A，Murray T，Stuart G，et al.Locating leaks from water supply pipes using the passive acoustic method［J］.Journal of Water Supply:Research and Technology AQUA，2005，54(8):519-530.

［2］李 鹤，杨 铎，闻邦椿，等.大型压缩机管道系统振动现场测试与控制［J］.振动与冲击，2007，26(4):158-160.

［3］孙立瑛，李一博，曲志刚，等.EMD信号分析方法的声发射管道泄漏检测研究［J］.振动与冲击，2007，26(10):161-164.

［4］周 琰，诸葛晶昌，封 皓，等.分布式光纤管道泄漏检测及预警技术研究［J］.仪器仪表学报，2008，29(8):1588-1591.

［5］Qu Z，Zhou Y，Zeng Z，et al.Detection of the abnormal events along the oil and gas pipeline and multi-scale chaotic character analysis of the detected signals［J］.Measurement Science＆Technology，2008，19(2):025301-1-8.

［6］Etter D M，Stearns S D.Adaptive estimation of time delay in sampled data systems［J］.IEEE Trans Acoustic，Speech，Signal Processing，1981，29(3):582-587.

［7］Djeddou M，Belouchranil A，Aouada S.Maximum likelihood angle-frequency estimation in partially known correlated noise for low-elevation targets［J］. SignalProcessing， IEEE Transactions，2005，53(8):3057-3064.

［8］Reed F，Feintuch P L，Bershad N J.Time delay estimation using the LMS adaptive filter-static behavior［J］.IEEE Trans Acoust，Speech，Signal Processin，1981，29(3):561-571.

［9］梁立涛，韩 峰，樊 昕，等.相干干扰对时延估计的影响研究［J］.探测与控制学报，2007，29(6):11-14.

［10］杨福生，洪 波.独立分量分析的原理与应用［M］.北京:清华大学出版社，2006.

［11］Hyvärinen A，Oja E.Independent Component Analysis:Algorithms and applications［J］.Neural Networks，2000，13(4-5):411-430.

［12］梁应敞，张贤达，李衍达，等.非高斯相关噪声中高斯信号的时延估计［J］.电子科学学刊，1997，19(5):606-612.

［13］Hyvärinen A.Fast and Robust Fixed-Point Algorithms for Independent Component Analysis［J］.IEEE Trans.on Neural Networks，1999，10(3):626-634.