树脂柱对复合材料夹层板屈曲及动力学性能的影响分析

朱 波，周 叮，刘伟庆

(南京工业大学 土木工程学院，南京 210009)

复合材料具有比强度高、比模量高、抗疲劳性好、抗震能力强、结构可设计性等优点，已在航天航空、汽车、建筑等各个领域得到了广泛的应用。复合材料夹层结构由面板和芯材通过树脂固化而成，在芯材上开凿贯穿厚度的圆孔，采用真空导入工艺，芯材中含有的圆柱状树脂柱能够更好地连接面板和芯材，提高面板与芯材之间的抗剥离和协调工作能力，起到类似于螺栓的作用，同时亦能提高芯材的受压受剪性能，称之为树脂柱点阵增强型复合材料。

过去对复合材料的研究大多集中于静力学分析和试验，近年来对复合材料的屈曲及动力学性能的研究已取得不少成果，如:Chen和Yang［1］用一阶剪切变形理论分析了层合梁的屈曲和自由振动，并用有限元法计算了层合梁的自振频率;文献［2］用解析法分析了考虑转动和剪切效应时复合材料夹层结构的自振频率。先进复合材料结构精细、工艺复杂周期长，以传统的方法研制费时费力，且难以得到准确而系统的科学结论，有限元数值模拟技术具有试验方法和理论解析不可比拟的优势，是研究结构力学性能的重要分析工具，ANSYS是目前有限元算法中较为流行的商业软件之一，已广泛应用于各种工程领域。

针对复合材料，ANSYS提供了一些特殊的壳单元及实体单元，目前对复合材料夹层结构主要采用这类单元进行模拟和分析［3－9］。但是，对于点阵增强型复合材料夹层结构，需考虑芯层树脂柱对整个结构的影响，这在已有单元中未能得到很好的考虑。文［10］将芯层树脂柱和泡沫分开划分单元，采用单胞概念，对含树脂柱的夹层板进行静力学分析，研究了树脂柱的分布和材性对层间界面应力分布及板竖向位移的影响。

本文对含有树脂柱的点阵增强型复合材料夹层板建立单胞分析模型，将芯层树脂柱与芯材分开，采用8节点SOLID45实体单元，应用ANSYS有限元软件研究树脂柱对夹层板的屈曲以及动力学性能的影响。

1 模型建立

图1所示为点阵增强型复合材料夹层板模型示意图，上下两层为面板，厚度为h1，中间芯层厚h2。对于点阵增强型轻质芯材，可认为芯材是由一系列单胞在空间排列组成，单胞由芯材基体及树脂柱共同构成，树脂柱呈圆柱状，在宏观结构中呈规则正交分布。每个单胞的边长为b，单胞中所含树脂柱直径为d。假设面板、芯材、树脂柱三者之间无粘结滑移，且未发生剥离现象，因此面板单元、芯材单元、树脂柱单元之间可采用位移协调式，各单元共用节点。

考虑一矩形复合材料夹层板，其尺寸为:长L1=800 mm，宽L2=320 mm，上下面板厚h1=5 mm，芯材厚h2=50 mm，单胞边长b=40 mm，树脂柱直径d=8 mm。

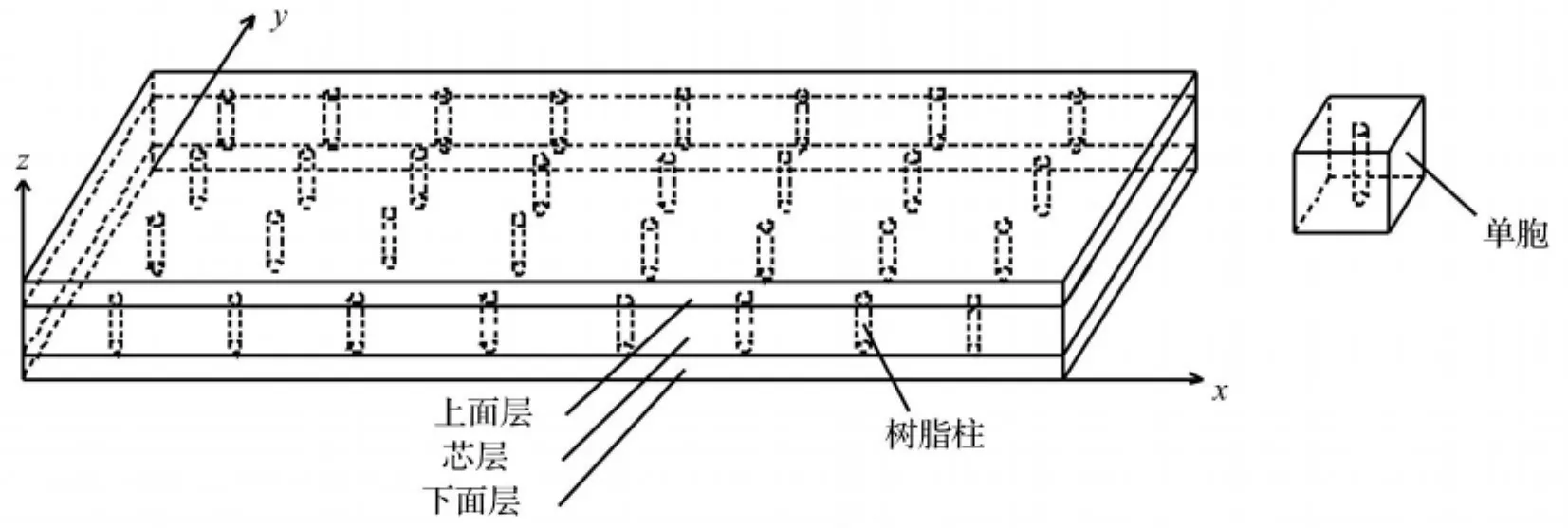
图1 点阵增强型复合材料夹层板示意图Fig.1 The schematic diagram of a sandwich plate with grooved perforation

纤维增强树脂基面板以平面内受力为主，采用四轴向［0/45/90/－45］的准正交玻璃纤维布，将面板定义为各向同性材料，并与一般铺设情况进行比较，对比结果见表1，误差在0.8%以内，可以忽略，故本文在后续分析中均将面板定义为各向同性材料以方便建立模型。芯材选用我国量大面广的泡桐木，面板、芯材及树脂柱的材料性质列于表2。本文研究不同边界条件下的夹层板:① 四边简支;② 两短边简支，另两边自由;③ 一短边固支，其余三边自由。采用8节点SOLID45三维实体单元，划分网格后的复合材料夹层板模型以及单胞局部网格划分示意图分别如图2、图3所示。

表1 各向同性与正交铺设时夹层板计算结果的比较Tab.1 Comparisons of isotropic and orthotropic results for a sandwich plate

表2 复合夹层板各组分材料性质Tab.2 Material properties of each component of the composite sandwich plate

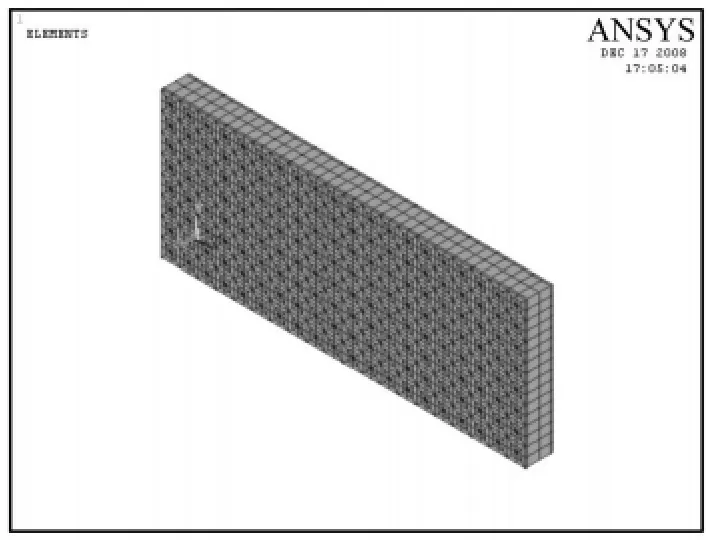
图2 复合材料矩形板ANSYS模型Fig.2 The meshing model of a sandwich plate

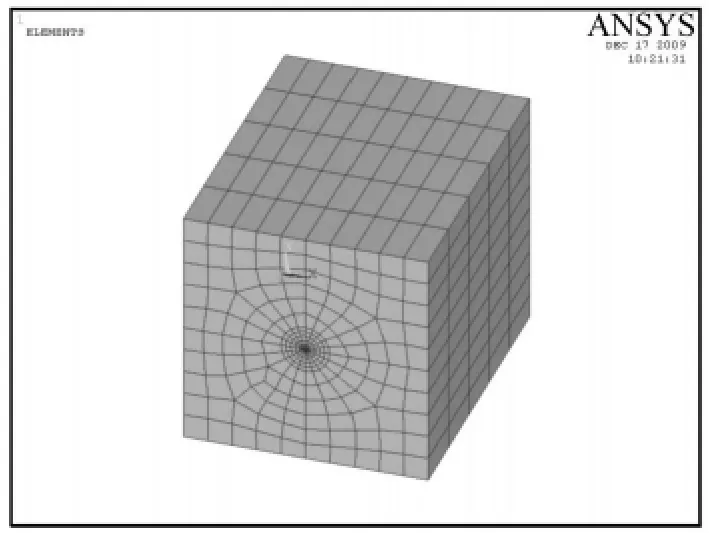
图3 单胞局部网格划分示意图Fig.3 The meshing model of one cell

2 树脂柱对夹层板屈曲性能的影响分析

2.1 树脂柱材性对夹层板屈曲性能的影响

考虑四边简支夹层板，承受平面内轴向载荷。保持单胞和树脂柱尺寸不变，改变树脂柱的弹性模量，表3给出了不同树脂柱弹模下夹层板的屈曲临界载荷。

表3 不同树脂柱弹模下夹层板的屈曲临界载荷Tab.3 Critical buckling loads of sandwich plates for different elastic modulus of resinic columns

从表中可以看出，树脂柱弹模越高，板的屈曲载荷值越大，然而，树脂柱弹模对复合材料板屈曲性能的影响并不显著。由表可知，树脂柱的弹模提高3倍(1500 MPa到4500 MPa)，屈曲临界载荷只提高了约2.6%，影响有限。

2.2 树脂柱分布对夹层板屈曲性能的影响

保持芯材树脂柱直径与单胞边长之比d/b=1/5不变，即树脂柱在芯层中的体积含量一定。改变芯层中树脂柱分布的疏密程度，即改变单胞底面边长b，表4给出了不同树脂柱间距对屈曲载荷的影响，其中b=∞表示芯层无树脂柱。从表中可以看出，当树脂柱间距变密(即b由160 mm变为40 mm时)，板的临界载荷提高了11.8%，比芯层无树脂柱时增大了13.7%，说明树脂柱的添加可提高复合材料夹层板的轴向承载能力，且树脂柱越密集，轴向承载力越大。

表4 不同树脂柱间距下夹层板的屈曲临界载荷Tab.4 Critical buckling loads of sandwich plates for different cell sizes

3 树脂柱对夹层板动力学性能的影响分析

3.1 树脂柱材性对夹层板自振频率的影响

材料性质及模型尺寸如前所述，研究两对边简支另两对边自由夹层板的无阻尼自由振动。改变树脂柱的弹性模量，表5给出了树脂柱弹模对板前五阶固有频率的影响。可以看出，树脂柱弹模越高，夹层板的固有频率越大，弹性模量的变化对各阶频率的影响大致相等，如:树脂柱的弹模提高3倍(1500 MPa到4500 MPa)，一至五阶频率均提高了约1.4%，可见树脂柱弹性模量的变化对夹层板自由振动特性的影响较小，且自振频率随树脂柱弹模的增加而呈缓慢线性增长趋势。

表5 不同树脂柱弹模下夹层板的前五阶自振频率Tab.5 First five natural frequencies of the sandwich plate for different elastic modulus of resinic columns

3.2 树脂柱分布对夹层板自振频率的影响

保持树脂柱在单胞中所占比例d/b=1/5不变，即树脂柱在芯层中的体积含量一定。改变芯层中树脂柱的疏密程度，即改变相邻树脂柱的间距b。表6给出了不同树脂柱疏密度下夹层板的前五阶固有频率，其中b=∞表示芯层无树脂柱。由表可知，随着树脂柱间距的变密，板的各阶固有频率均随之增大，且低阶频率的变化更为显著，如:当b由160 mm变为40 mm时，板的一阶频率提高了28.1%，比芯层无树脂柱时增大了29.2%;第五阶频率提高了24.5%，比芯层无树脂柱时增大了25.9%。可见，树脂柱分布疏密程度对夹层板自振频率有明显影响。图4－图6给出了b=40 mm时夹层板的前三阶自由振动模态。

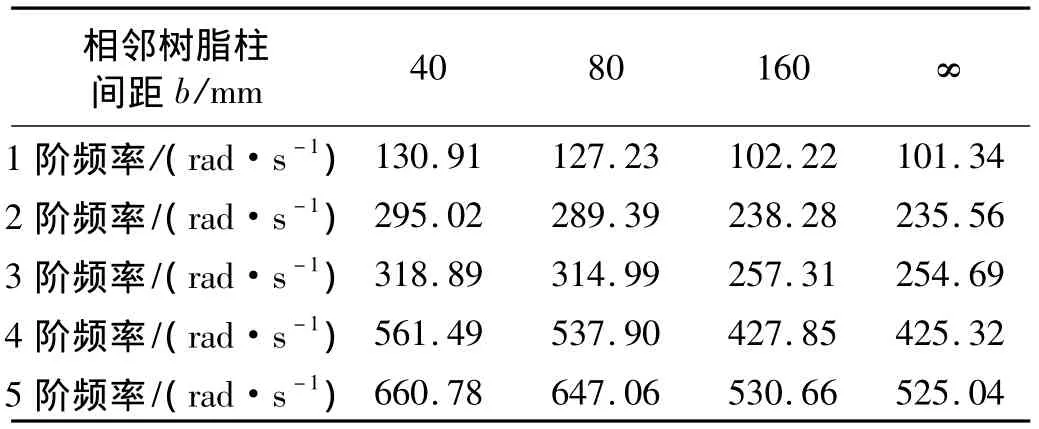
表6 不同树脂柱间距下夹层板的前五阶自振频率Tab.6 First five frequencies of sandwich plate for different cell sizes

3.3 树脂柱对夹层板瞬态动力学性能的影响

考虑一短边固支，其余各边自由的夹层板，自由短边的中点承受在有限上升时间内的平面外瞬态冲击力，从t=0时刻开始，载荷初始值为0，当t=0.075 s时达到最大值20 kN，加载结束时间为t=1 s，加载过程如图7所示。

图4 夹层板自由振动的第一阶模态Fig.4 Fundamental mode shape of the sandwich plate

图5 夹层板自由振动的第二阶模态Fig.5 Second mode shape of the sandwich plate

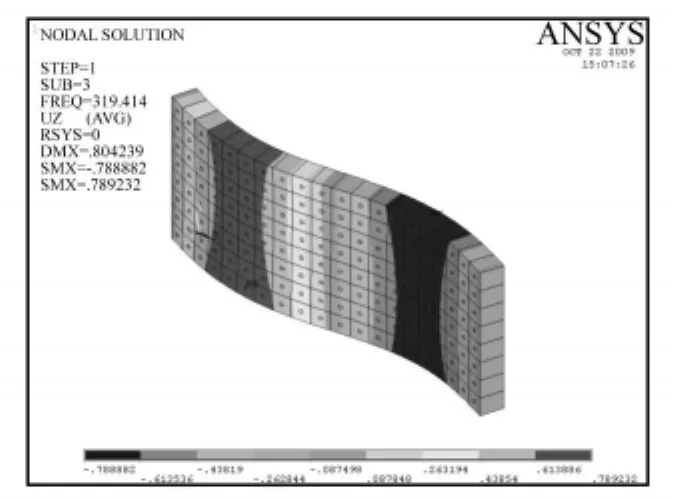
图6 夹层板自由振动的第三阶模态Fig.6 Third mode shape of the sandwich plate

图7 瞬态荷载1秒内的加载过程Fig.7 Transient loading process within 1 second

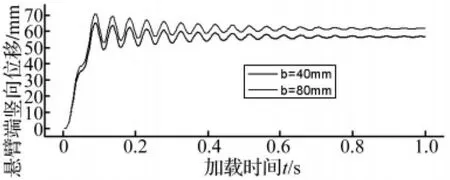
图8 夹层板悬臂端中点处竖向位移随时间的变化曲线Fig.8 Vertical displacement at cantilever end of the plate

图9 不同树脂柱间距下板中线下沿的最大振幅曲线Fig.9 Maximum amplitude of the plate for different cell sizes

考虑树脂的粘弹性性质及周围空气阻力的影响，引入阻尼，取等效粘性阻尼系数c=8 kN·s/m。图8给出了b=40 mm及b=80 mm时，悬臂端中点处竖向位移随加载时间的变化曲线，可以看出，当 t=0.088 s时位移达到最大值。图9给出了不同树脂柱间距下，t=0.088 s时夹层板中线下沿的竖向振幅曲线。从图中可以看出，悬臂端振幅最大，且随树脂柱间距变密而减小，当b由80 mm变为40 mm时，悬臂端振幅减小了约6.9%，比无树脂柱时降低了约8.7%。可见，在瞬态荷载作用下，树脂柱对于降低夹层板的竖向动力位移有一定的作用。

4 结论

本文应用ANSYS有限元软件分析了树脂柱点阵增强轻木芯材复合面板屈曲载荷、自由振动以及瞬态响应的影响。分析结果表明，树脂柱对板的力学性能有一定的贡献，其中材料特性对夹层板屈曲及动力学特性的影响有限，可以忽略;而芯层树脂柱分布疏密程度的变化对点阵增强型夹层板的屈曲及动力学特性有较大影响;此外，树脂柱的添加对于减小瞬态荷载作用下夹层板的竖向动力位移有一定的积极作用。可见，为提高夹层板的力学性能，合理安排树脂柱的分布要比单纯增大其弹性模量效果更好，研究结果可以为点阵增强型复合材料夹层板的参数设计提供依据。

［1］Chen A T，Yang T Y.Static and dynamic formulation of symmetrically laminated beam finite element for a microcomputer［J］.J Comp Mat，1995，19:459 －475.

［2］Chandrashekhara K，Krishnamurthy K，Roy S.Free vibration of composite beamsincluding rotary inertia and shear deformation ［J］. Composite Structures， 1990， 14:269－279.

［3］况 祺，夏凌辉，常春伟.ANSYS在复合材料夹层结构屈曲分析中的应用［J］.科学技术与工程，2005，5(32):1836－1838.

［4］石建军，吴东辉，迟 波，等.Shell91单元在复合材料蜂窝夹层结构分析中的应用［J］.纤维复合材料，2006，3:40－42.

［5］李 涛，樊庆文.ANSYS在复合材料应力分析中的应用［J］.机械，2006，12(33):47－48.

［6］廖英强，苏建河，柯善良，等.ANSYS在复合材料仿真分析中的应用［J］.玻璃纤维，2006，4:21－26.

［7］廖 原.ANSYS在复合材料梁设计中的应用［J］.广东建材，2007，12:96－98.

［8］Zhang S H，Chen H L.A study on the damping characteristics of laminated composites with integral viscoelastic layers［J］.Composite Structures，2006，1(74):63 －69.

［9］Barbero E J， Lonetti P， Sikkil K K. Finite element continuum damage modeling ofplain weave reinforced composites［J］.Composites Part B:Engineering，2006，2－3(37):131－147.

［10］姚秀冬，周 叮，刘伟庆.复合材料夹层板树脂柱的影响［J］.材料科学与工程学报，2009，27(6):1－6.