悬浮隧道锚索黏弹性阻尼器的最优阻尼系数

孙胜男，陈健云，苏志彬

(1. 聊城大学 建筑工程学院，山东 聊城，252059；2. 大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连，116024)

锚索是悬浮隧道的重要构件，其动力特性对悬浮隧道的正常运营至关重要。前期工作表明：悬浮隧道锚索在参数激励、涡街等作用下可能发生大幅振动[1-5]。然而，悬浮隧道是一种新兴的交通方案，目前关于锚索振动控制的研究几乎没有，与锚索受力性质相似的斜拉索的振动控制研究相对较多。Pacheco等[6]用 Galerkin方法建立索-油阻尼器系统的振动常微分方程，得到使斜拉索各阶模态阻尼达到最大阻尼系数和最大模态阻尼比的通用设计曲线。Tabatabai等[7]考虑斜拉索的抗弯刚度和垂度的影响，用差分方法得到索-阻尼器系统的面内振动模态阻尼比及最优阻尼器系数。Main等[8-9]对系统的频率变化进行分析，研究斜拉索的振幅、模态阶数对最优阻尼的影响。Johnson等[10-11]对斜拉索–MR阻尼器系统的半主动控制进行研究。Wang等[12-13]研究黏性阻尼器和磁流变阻尼器对斜拉索的振动控制。邬喆华[14]基于位移和速度反馈对斜拉索进行半主动控制的数值仿真计算。本文作者采用在锚索近端部施加黏弹性阻尼器来控制锚索的振动，根据悬浮隧道锚索的特点，以考虑Irvine参数[15]的锚索和黏弹性阻尼器组成的系统为研究对象，建立锚索-黏弹性阻尼器的振动方程，通过伽辽金法得到系统的振动常微分方程，然后进行复特征值分析，得到锚索可能达到的最优阻尼比以及相应的最优阻尼器系数，分析锚索的倾角和垂度对锚索最优阻尼比的影响。

1 锚索-黏弹性阻尼器系统的数学模型

1.1 振动方程

锚索-黏弹性阻尼器系统的数学模型如图1所示。锚索在静力荷载作用下的平衡状态为振动分析的初始构形，表示为Z=[x(s) y(s)]T，s为弧长坐标。锚索的动力响应以初始构形为参考构形，表示为：

其中：t 为时间。

由Hamilton原理建立系统的能量方程：

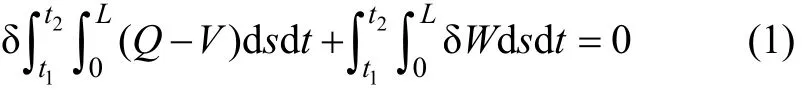
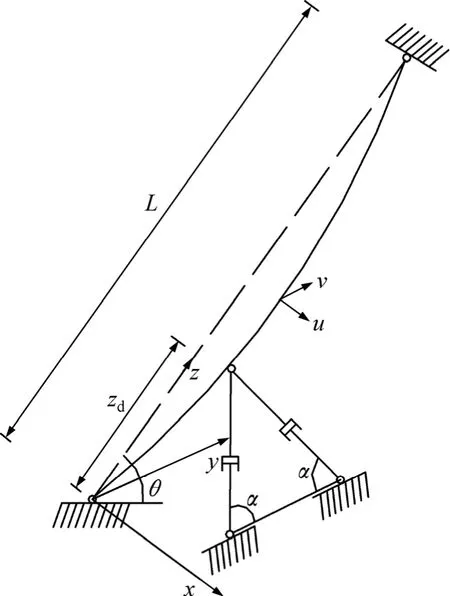
图1 锚索-阻尼器振动模型Fig.1 Tether-damper vibration model

式中：δ为变分符号；t1和t2分别为时间上限和下限；L为锚索无应力状态的长度；Q为动能密度；V为弹性应变能密度；δW为外力作用下的虚功密度。

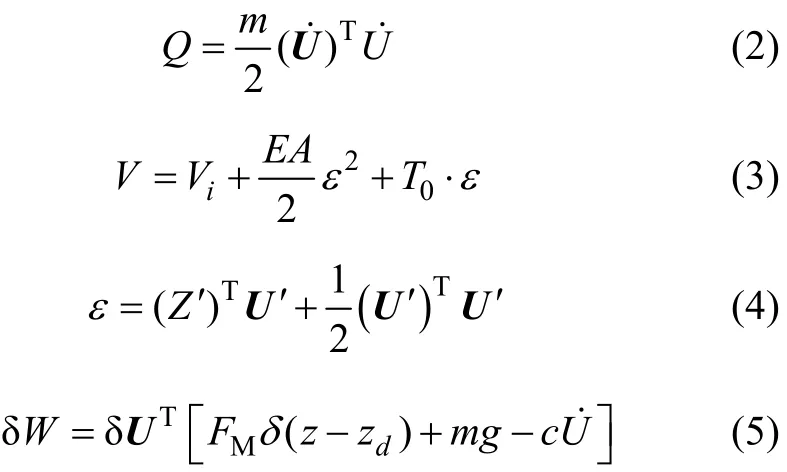
式中：m为锚索单位长度质量；Vi为初始构形的弹性应变能密度；E为锚索的弹性模量；A为锚索横截面积；ε为Lagrangian应变；T0为静力状态下锚索的张力；FM为阻尼器作用在索上的力，FM=[FMxFMy]T；δ(·)为 Dirac delta函数；zd为图 1所示的阻尼器位置；c为锚索的黏性阻尼系数，c=diag[cxcy]。

假定锚索的初始构形为二次抛物线，即满足

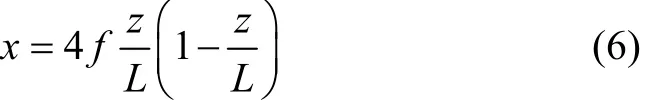
将式(2)～(6)代入式(1)，略去静载的平衡项、高阶微量，z向运动的小量，得：

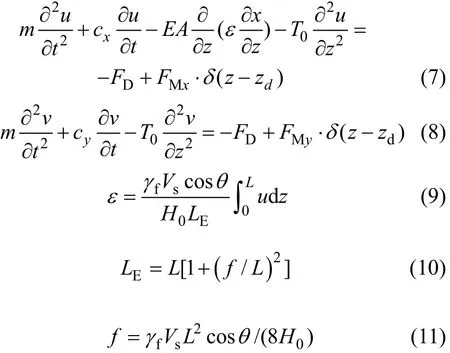
式中：FD为锚索振动时，水体对其单位长度上的作用力；γf为锚索的浮容重；Vs为锚索单位长度的体积；H0为沿 z向的锚索初张力，T0≈H0；LE为静力作用下锚索的长度；f为锚索跨中垂度；θ为锚索的倾角。

式(7)和式(8)分别为面内、面外振动方程，由于2个方程类似，本文仅对式(7)进行分析。

由Morison公式，锚索振动时水体对其单位长度上的作用力[3]为：

式中：Dt为锚索的直径；ρw为水的密度；Cm为附加质量系数，取Cm=1；CD为拖拽力系数，取CD=0.7。

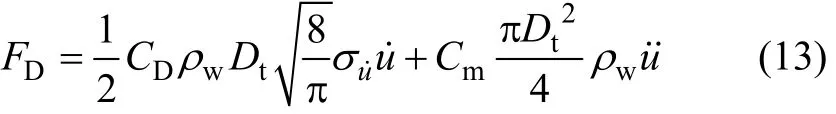
式中：σu˙为u˙的方差。

阻尼器对锚索的作用力 FMx由几何变换关系可得：

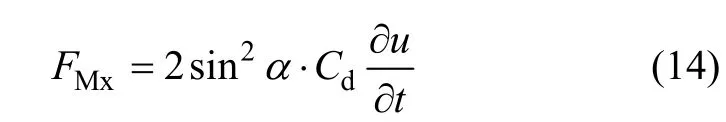
式中：α为阻尼器倾角；Cd为阻尼器系数。

最终式(7)变为：

式中：m为锚索单位长度质量和水体附加质量之和。

取锚索的振动模态为标准弦的振动模态，即

用伽辽金法将偏微分方程变为常微分方程：

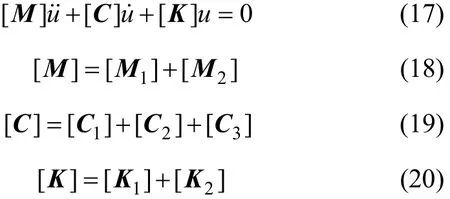
式中：[M1]和[M2]分别为锚索的质量矩阵和附加质量矩阵；[C1]，[C2]和[C3]分别为锚索的阻尼矩阵、水体提供的阻尼矩阵和阻尼器提供的阻尼矩阵；[K1]和[K2]分别为初张力、动张力提供的等效刚度矩阵。

1.2 方程求解

设方程的解有如下形式：

将式(21)代入式(17)，消去共因子后，得：

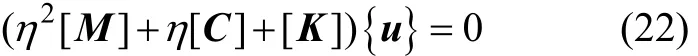
其中：{u}=[u1，u2，…，un]T。

当且仅当 det|(η2[M]+η[C]+[K]|=0 时，方程(22)具有非平凡解。当η为2n次时，可以确定2n个特征值ηi(1，2，…，2n)。

引入恒等式：

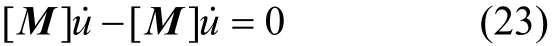
与式(17)联立后，写为：

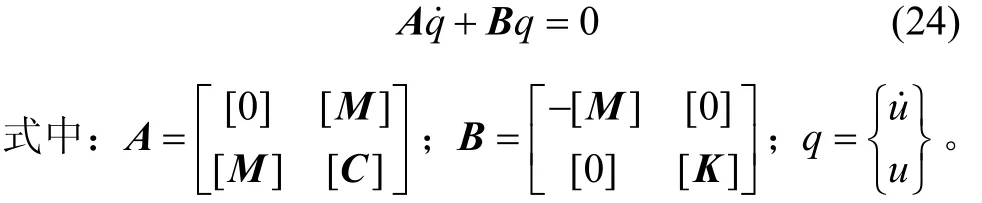
令

代入式(24)得：

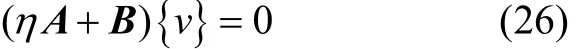
这一方程具有非零解的条件是det|ηA+B|=0。用双重步QR算法求解，可得到系统的2n个成对的共轭复特征值，第i对复特征值的实部和虚部分别对应系统的第i阶振型的2个信息，即阻尼比和频率。

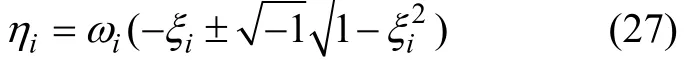
对于面外振动式(8)的求解只要令[K2]矩阵为 0，其他求解过程与面内振动式(7)的求解过程相同。

本文根据上述理论，在MATLAB里编制了锚索–阻尼器系统动力求解程序，并用此程序进行数值分析。

2 数值算例及结果分析

锚索安装阻尼器后，由于集中阻尼力的作用，锚索的振型和无阻尼器锚索的振型是不同的。当阻尼器提供的阻尼力为0时，锚索的振型和无阻尼器锚索振型一样。而当阻尼器阻尼趋于无穷大时，该点成为支点，相当于锚索变短，固有频率增大，阻尼的量变引起振动形态的质变，阻尼器不耗散能量，从而锚索也就得不到有效的减振。因此，为使锚索得到很好的振动控制，必须选择最优的阻尼值。

为使结果便于讨论，引进以下无量纲参量[6,15]：

式中：λ2为反映锚索垂度及拉伸性能的无量纲参数；Bi为与锚索振动模态有关的黏弹性阻尼器阻尼系数的无量纲参数；ω01为不考虑垂度影响时无阻尼锚索的面内一阶振动频率。

悬浮隧道的基本参数取值如表1所示。

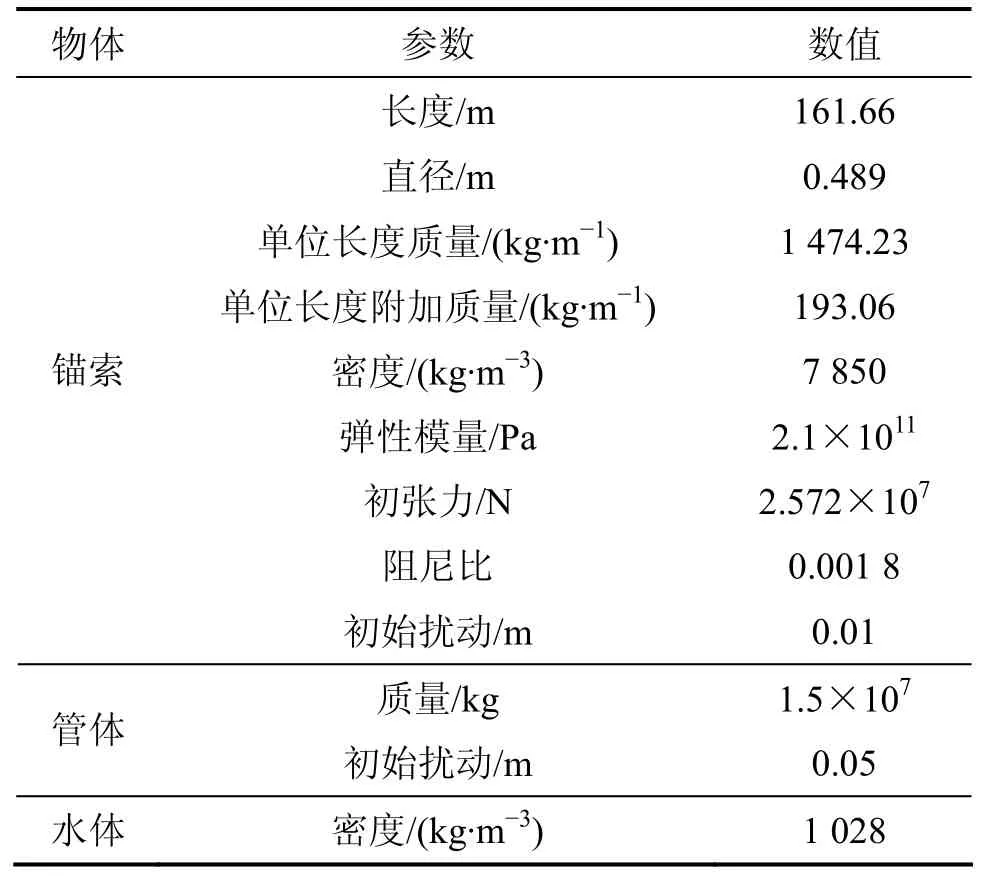
表1 悬浮隧道的基本参数Table 1 Basic parameters of submerged floating tunnel

2.1 锚索的最大模态阻尼比及最优阻尼器系数

安装阻尼器后，锚索达到最优阻尼比时阻尼器系数的取值，可以为阻尼器的设计提供依据。本节取阻尼器倾角 α为 45°，阻尼器作用位置到索端的距离和整根锚索的比zd/L=0.030 9，锚索倾角为60°，不断改变阻尼器系数以求出系统可能达到的最优阻尼比。分别计算了锚索面内、外前4阶模态，结果如图2所示。

锚索的模态阻尼比由2部分组成：一为水体提供的模态阻尼比，二为阻尼器提供的模态阻尼比。由图2可以看出：水体提供的面内前四阶模态阻尼比分别为0.031 9，0.017 4，0.011 6，0.008 7；水体提供的面外1阶模态阻尼比为0.037 2，面外2～4阶模态阻尼比和面内2～4阶对应的模态阻尼比相等，垂度使得面内一阶模态阻尼比比面外一阶模态阻尼比稍小。

为了更加清晰地了解阻尼器提供的最优模态阻尼比，本文仅考虑阻尼器提供的阻尼，不考虑水体提供的阻尼，研究系统可能达到的最优阻尼比，如图 3所示。

由图3可以看出：阻尼器提供的面内一阶模态最优阻尼比为0.012 5，面内高阶及面外模态最优阻尼比均为0.017 0左右；达到最优的阻尼比时，面内一阶模态的 Bi为 0.1，而面内高阶模态和面外模态的 Bi为0.11。虽然各阶模态达到最优阻尼比时的Bi相近，但是由式(29)可知：最优阻尼器系数Cd的值是不同的，模态阶数越高，对应的最优阻尼器系数Cd就越小。所以，在设计阻尼器时应首先确定锚索欲控制的模态阶数，以便得到最好的控制效果。

2.2 锚索倾角对锚索最优模态阻尼比的影响

图4所示为水体和阻尼器共同作用下锚索最优模态阻尼比与锚索倾角的关系，本节取阻尼器倾角α为45°，zd/L=0.030 9。

从图4可以看出：锚索的面内一阶模态最优阻尼比随着倾角的增大而逐渐增大，而锚索的面内高阶模态和面外模态最优阻尼比随着倾角增大没有明显的变化。可见锚索倾角的改变只会影响锚索的面内一阶模态最优阻尼比，而对锚索的高阶模态及面外模态最优阻尼比没有影响。

2.3 锚索垂度对锚索最优模态阻尼比的影响

图5所示为水体和阻尼器共同作用下锚索最优模态阻尼比和锚索垂度的关系，本节取阻尼器倾角α为45°，zd/L=0.030 9，通过改变锚索的倾角改变垂度。

图2 模态阻尼比和Bi的关系Fig.2 Relationship between modal damping ratios and Bi

图3 阻尼器单独作用时模态阻尼比与Bi的关系Fig.3 Relationship between modal damping ratios and Bi under damper

图4 模态最优阻尼比与倾角的关系Fig.4 Relationship between optimal modal damping ratios and inclination

图5 模态最优阻尼比与垂度的关系Fig.5 Relationship between optimal modal damping ratios and sag

从图5可以看出：随着锚索垂度增大，面内一阶模态最优阻尼比逐渐减小，而锚索的面内高阶模态和面外模态最优阻尼比没有明显的变化。

3 结论

(1) 建立悬浮隧道锚索–黏弹性阻尼器系统的数学模型，以此为基础得出锚索-黏弹性阻尼器的振动方程，然后通过复特征值分析得到锚索的最优模态阻尼比。

(2) 锚索各阶模态达到最优阻尼比时对应的最优阻尼器系数不同。模态阶数越高，对应的最优阻尼器系数越小。设计阻尼器时应首先确定锚索欲控制的模态阶数，以便得到最好的控制效果。

(3) 锚索垂度的存在，使得锚索的面内一阶模态最优阻尼比比面内高阶模态和面外模态稍小，而面内高阶模态和面外模态的最优阻尼比基本相同。

(4) 对于水体提供的锚索模态最优阻尼比，面内面外均以一阶模态的为大。随着模态的增大，水体提供的最优模态阻尼比逐渐减小。

(5) 锚索的面内一阶模态最优阻尼比随着锚索倾角的增大而增大，随锚索垂度的增大而减小。

(6) 锚索倾角、垂度的变化仅影响锚索的面内一阶模态最优阻尼比，对面内高阶模态及面外模态最优阻尼比无影响。

[1] 孙胜男, 陈健云, 苏志彬. 悬浮隧道锚索-隧道耦合非线性参数振动研究[J]. 振动与冲击, 2007, 26(10): 104-108.SUN Sheng-nan, CHEN Jian-yun, SU Zhi-bin. Study on nonlinear parametric vibration of a tether-tube coupled and submerged floating tunnel[J]. Journal of Vibration and Shock,2007, 26(10): 104-108.

[2] SUN Sheng-nan, CHEN Jian-yun, LI Jing. Non-linear response of tethers subjected to parametric excitation in submerged floating tunnels[J]. China Ocean Engineering, 2009, 23(1):167-174.

[3] 陈健云, 王变革, 孙胜男. 悬浮隧道锚索的涡激动力响应分析[J]. 工程力学, 2007, 24(10): 186-192.CHEN Jian-yun, WANG Bian-ge, SUN Sheng-nan. Analysis of vortex-induced dynamic response for the anchor cable of submerged floating tunnel[J]. Engineering Mechanics, 2007,24(10): 186-192.

[4] 孙胜男, 陈健云. 悬浮隧道锚索多阶涡激非线性振动[J]. 大连海事大学学报, 2007, 23(4): 86-90.SUN Sheng-nan, CHEN Jian-yun. Multi-order vortex-induced nonlinear vibration of submerged floating tether[J]. Journal of Dalian Maritime University, 2007, 23(4): 86-90.

[5] 陈健云, 孙胜男, 苏志彬. 流作用下悬浮隧道锚索的动力响应[J]. 工程力学, 2008, 25(10): 229-234.CHEN Jian-yun, SUN Sheng-nan, SU Zhi-bin. Dynamic response of submerged floating tunnel tethers subjected to current[J]. Engineering Mechanics, 2008, 25(10): 229-234.

[6] Pacheco B M, Fujino Y, Sulekh A. Estimation curve for modal damping in stay cables with viscous damper[J]. Journal of Structural Engineering, 1993, 119(6): 1961-1979.

[7] Tabatabai H, Mehrabi A B. Design of mechanics viscous dampers for stay cables[J]. Journal of Bridge Engineering, 2000,5(2): 114-123.

[8] Main J A, Jones N P. Evaluation of viscous dampers for stay-cable vibration mitigation[J]. Journal of Bridge Engineering,2001, 6(6): 385-397.

[9] Main J A, Jones N P. Free vibration of taut cable with attached damper.Ⅰ: linear viscous damper[J]. Journal of Engineering Mechanics, 2002, 128(10): 1062-1071.

[10] Johnson E A, Christenson R E, Spencer B F. Semi-active damping of cables with sag[C]//Advances in Structure Dynamics.San Diego: Elsevier Science Ltd, 2000: 327-334.

[11] Johnson E A, Christenson R E. Semiactive damping of cables with sag[J]. Computer-aided Civil and Infrastructure Engineering, 2003, 18(2): 132-146.

[12] Wang X Y, Ni Y Q, Ko J M, et al. Optimal design of viscous dampers for multi-mode vibration control of bridge cables[J].Engineering Structures, 2005, 27(5): 792-800.

[13] Duan Y F, Ni Y Q, Ko J M. Cable vibration control using magnetorheological dampers[J]. Journal of Intelligent Material Systems and Structures, 2006, 17(4): 321-325.

[14] 邬喆华. 磁流变阻尼器对斜拉索振动控制的研究[D]. 杭州:浙江大学建筑工程学院, 2003: 1-113.WU Zhe-hua. Vibration control of stay-cable using magnetorheological damper[D]. Hangzhou: Zhejiang University.Institute of Architectural and Civil Engineering, 2003: 1-113.

[15] Irvine H M. Cable structures[M]. Cambridge: Massachusetts Institute of Technology Press, 1981: 95-130.

[16] 马海龙. 基于黏弹性阻尼器的海洋平台振动控制[D]. 青岛:中国海洋大学工程学院, 2003: 18-20.MA Hai-long. Vibration control of offshore platform with viscoelastic dampers[D]. Qingdao: Ocean University of China.College of Engineering, 2003: 18-20.