基于FLAC3D的复杂条件下露天转地下开采空区围岩变形及破坏特征

史秀志，黄刚海，张舒，周健

(中南大学 资源与安全工程学院，湖南 长沙，410083)

矿体由露天转地下开采是目前国内部分露天矿面临的主要技术问题之一，而且这一问题随着矿体开采向深部延伸会更为突出。露天转地下开采工艺参数对地下采矿的安全性及矿产资源的损失量产生直接影响，国内外很多学者在此方面取得了许多研究成果，如：南世卿等[1]采用 RFPA数值模拟程序分析断层影响下露天转地下境界矿柱稳定性；韩现民等[2]采用数值模拟技术分析露天转地下矿山边坡稳定性；田泽军等[3]研究了露天转地下开采前期关键技术措施。湖北铜绿山铜铁矿Ⅰ号矿体原为露天开采，露天坑闭坑后，其下部仍有深部残矿，矿石储量约26.15万t，金属量Cu为3 280 t，Te为10.13万t，具有较高的回收价值。对该残矿，矿山拟用地下开采方案。由于该残矿开采环境极其复杂，研究空区围岩变形及破坏特征对指导矿山露天转地下开采具有重大意义。为此，本文作者针对Ⅰ号矿体露天转地下开采的实际情况，采用FLAC3D数值方法模拟各种工艺参数下的开挖过程，用FLAC3D软件内嵌FISH语言定义岩石剪切破坏判据值Fs，动态监测空区关键位置的Fs和拉应力，以确定境界矿柱破坏原因是剪切破坏还是拉伸破坏；对不破坏的空区，观察顶板下沉量及围岩塑性变形情况，分析围岩变形特征，以确定合理的采矿工艺参数，从而为施工设计提供依据和指导。

1 工程概况

铜绿山铜铁矿是湖北大冶有色金属公司属下的一个大型主体铜金属矿山，也是全国重点铜基地之一。全矿区共有12个矿体，其中主矿体4个，分别为Ⅰ，Ⅱ，Ⅲ和Ⅳ号矿体，其中：Ⅰ和Ⅱ号矿体为露天开采，Ⅲ和Ⅳ为地下开采。图1所示为矿山12号勘探线剖面示意图。

矿山露天南坑开采对象为Ⅰ和Ⅱ号矿体，设计开采深度为-185 m，其中Ⅱ号矿体已采完，Ⅰ号矿体大概实际开采至-187 m。由于深部开采难度大、效率低，加上汛期影响，露天南坑开采于2005年结束。闭坑实际标高-187 m，闭坑时坑底面积约1 400 m2，汇水面积约45.8万m2，露天坑边缘平均标高约+40 m。

Ⅰ号矿体深部残矿分布在10～16线、-187～-425 m标高间，大部分赋存于-275 m以上(图1所示)；矿体厚度为 5～35 m；矿体走向长度为 110 m，倾角为60°～80°。矿体上盘为斜长石岩、矽卡岩，稳固性较差；下盘及矿体多为大理岩，中等稳固；北端上盘受一断层影响，断层贯穿露天坑，强度低，可能导水，对残矿的安全回收影响较大。南坑闭坑后作为北露天坑采矿的排土场，由于未能及时排水，南坑积蓄大量水体，积水深度可达40 m，积水与回填土混合，使回填土底层形成泥沙，强度较低。回填土上表面历史最大标高为-113 m(即露天南坑内回填土厚度已达74 m)。

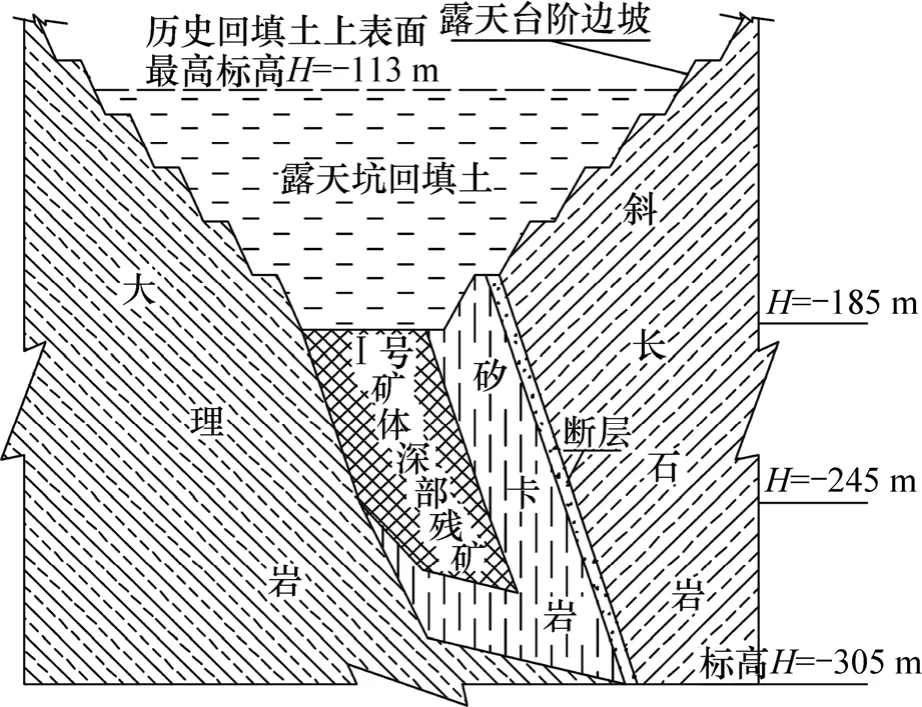
图1 12号勘探线剖面示意图Fig.1 No.12 exploration line profile schematic diagram

2 数值模拟思路及方法

FLAC3D是美国 ITASCA咨询集团公司开发的三维快速拉格朗日分析程序，是二维有限差分程序FLAC2D的扩展，能够进行岩石、土质和其他材料在达到屈服极限后经历塑性变形的三维空间行为分析，为采矿岩土工程领域求解三维问题提供了一种理想的分析工具[4-5]。

2.1 数值模拟思路及目的

(1) 根据矿体赋存条件，建立矿体开挖环境的FLAC3D模型。

(2) 赋予模型材料力学参数，通过运算求解，生成模型初始应力场。

(3) 定义开挖范围为空模型(null)，通过运算求解，模拟开挖过程。空区开挖模拟的目的及实现该目的的方法如下：

① 分析空区围岩变形特征：监测关键位置的位移，分析监测结果，并观察空区围岩塑性变形区。

② 确定空区顶板的破坏形式是拉伸破坏还是剪切破坏：监测关键位置的拉应力，将监测结果与材料抗拉强度对比，可确认材料是否拉伸破坏。

由于材料抗剪强度跟随单元体受力状态的变化而变化，故不能通过对比剪应力和抗剪强度来判断单元体是否发生剪切破坏。应采用材料的剪切破坏判据来判断。FLAC3D模型中岩石单元体发生剪切破坏的摩尔-库仑判据为[6-9]：式中：Fs为剪切破坏阀值；σ1和σ3分别为最大主应力和最小主应力(压应力时为正)；C为内聚力；φ为内摩擦角。当Fs＞0时，单元体未发生剪切破坏；当Fs≤0时，单元体发生剪切破坏。

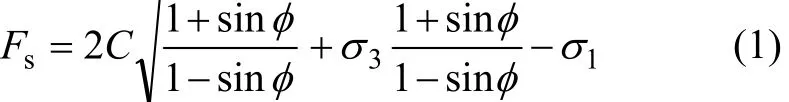
由于 FLAC3D内部程序没有定义岩石剪切破坏的摩尔-库仑判据Fs值，为实现Fs在运算过程中的动态监测，以确定单元体在某个时刻是否发生剪切破坏，应用FLAC3D内嵌 FISH语言，按式(1)编写程序定义Fs为模型单元体剪切破坏的摩尔-库仑判据值。通过监测关键位置的Fs，可判断单元体是否发生剪切破坏。

③ 分析跨度对空区围岩的影响：选择一安全厚度的立柱(相邻空区间用于支撑顶板的隔离矿柱)，确保空区破坏不是立柱破坏所致，模拟不同跨度的开挖过程，分析跨度对空区围岩变形及破坏特征的影响。

④ 分析立柱厚度对空区围岩的影响：以一空区跨度为代表，模拟不同立柱厚度下的开挖过程，分析立柱厚度对空区围岩变形及破坏特征的影响。

(4) 综合分析模拟结果，根据空区围岩变形及破坏特征确定合理的地下采矿工艺参数。

2.2 建模

初步确定垂直于12号勘探线布置2个采场。由于采场跨度相对于采场长度要短很多，故可取12号勘探线所切剖面建立模型，采场走向方向取1 m作为模型厚度，将三维模型转化为二维模型进行研究。考虑Ⅰ号矿体深部残矿全部回采将历时4 a，回采期间露天北坑继续向南坑填土，预计4 a间露天坑回填土加高约70 m，故模型考虑露天坑内回填土厚度150 m。模型高度268 m，宽度300 m，如图2所示。

2.3 模型初始应力场的生成

将模型定义为摩尔-库仑模型，赋予材料力学参数，加重力，固定边界，设置力不平衡比率为5×10-7，用 solve求解至平衡，可得模型的初始应力场。有关计算的材料力学参数如表1所示。

图2 矿体开挖环境的FLAC3D模型Fig.2 FLAC3D model of orebody excavating environment

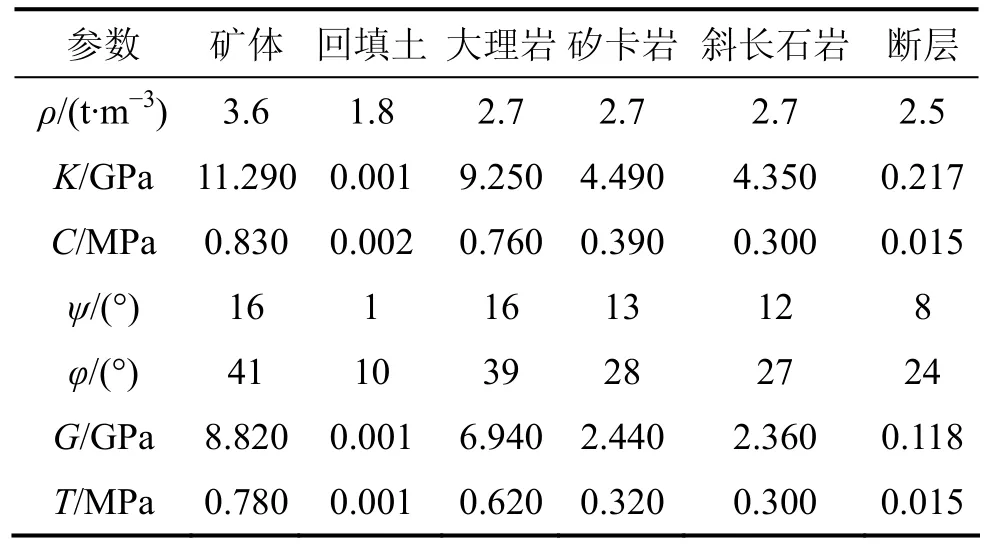
表1 模型材料力学参数Table 1 Model material mechanics parameters

2.4 开挖模拟

2.4.1 空区开挖方式

Ⅰ号矿体深部残矿赋存条件较恶劣。为确保安全，决定采用上向分层胶结充填采矿法，分层高度为3 m，采用两采一充方式，控顶高度为6 m。垂直于12号勘探线布置2个采场，采场跨度控制在16 m以下，2个采场之间保留厚度约5 m的条带矿柱(称立柱)，用于支撑顶板，如图3所示。

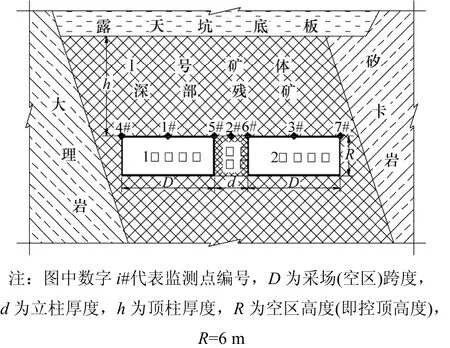
图3 空区开挖及其监测点布置示意图Fig.3 Diagram of goaf excavating and monitoring points’ places

开挖模拟从-239 m标高开始，采用每3 m 1个分层向上回采，即开挖第1步的采空区底板标高为-239 m，顶板标高为-233 m，顶板距离露天坑底板(下称顶柱)46 m；之后充填3 m，接着上采3 m，又形成6 m高的空区，顶柱厚43 m；依此类推，采场空区以3 m一步往上移动。

2.4.2 关键点及其监测参数确定

根据地下矩形坑道围岩应力分布特点，通常平直边容易出现拉应力，转角处产生较大剪应力集中[9]。由此可判定，采空区破坏的方式可能有以下几种：空区顶板受拉破坏；立柱破坏；空区顶板两端剪切破坏。

根据上述采空区破坏模式，为便于对模拟结果进行分析，在模拟过程中，选择以下关键点(见图3)及其相关参数进行监测：

(1) 分别监测1号和2号采场顶板中点(1号和3号监测点)水平应力及其垂向位移(以下简称位移)，用history命令记录精确值，以便读取。

(2) 监测立柱顶部(2号监测点)位移，用history命令记录其精确值；

(3) 分别监测1和2号采场顶板端部(监测点4～7号)的Fs随时间步的变化情况，并用history命令将Fs曲线上各点的坐标保存在表格中，用于查看Fs达到0时的时间步。

3 开挖模拟结果分析

设n表示FLAC3D程序运算的时间步，n(i)表示第i号监测点的时间步。

3.1 立柱厚度d一定、跨度D不同时开挖模拟结果及分析

粗略的模拟结果显示，当d=5 m时，空区破坏不是立柱破坏所致，故取d=5 m，模拟各种跨度下空区不断上移(其顶柱厚度从46 m逐渐减小到4 m)过程中其围岩变形及破坏情况。

3.1.1 监测点位移分析

表2所示为d=5 m和D=16～8 m时各监测点铅垂方向的位移。

从表2可以看出：随着顶柱厚度逐渐减小，各监测点的位移均先减小，后增大，且增大的速度远超过先前减小的速度；在同一跨度下，3个监测点位移增大速度开始明显加快时对应的顶柱厚度是一致的(即表2中，D相同的3列数中，加粗的数据在同一行)。为便于表述，在此定义：当立柱厚度d为i m、空区跨度D为j m时，在顶柱厚度h不断减小过程中，各监测点的位移增大速度开始明显加快时对应一个顶柱厚度，称该顶柱厚度为关键顶柱厚度，用hi,j表示。从表2可知：h5,16=28 m，h5,14=25 m，h5,12=22 m，h5,10=19 m，h5,8=16 m。

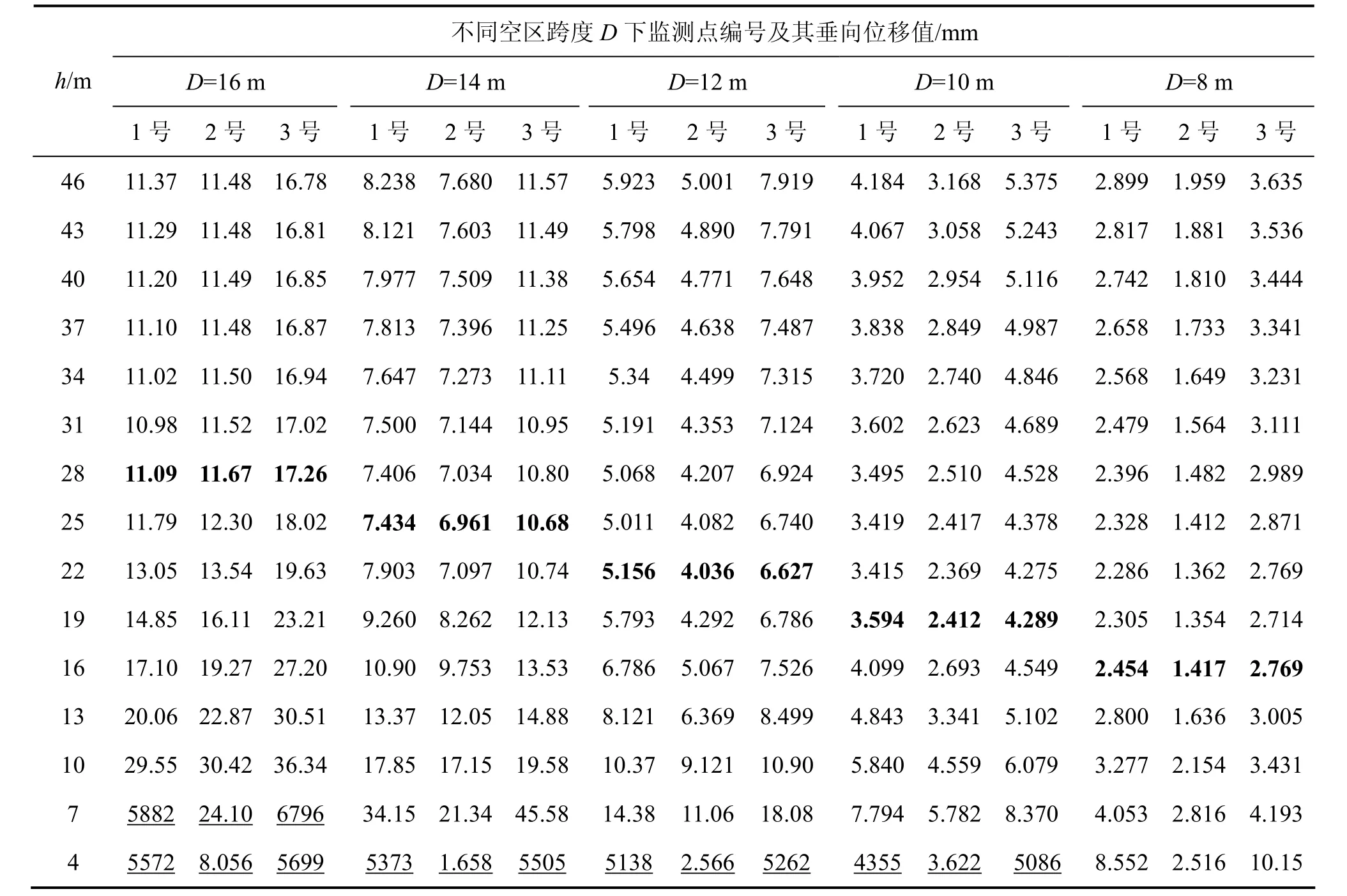
表2 d=5 m时不同跨度下各监测点位移Table 2 Displacement of monitoring points under different spans when d=5 m

3.1.2 空区围岩塑性变形分析

图4所示为D=16 m时不同顶柱厚度下空区围岩塑性变形情况(仅以 D=16 m 为例，其他跨度规律相似)。

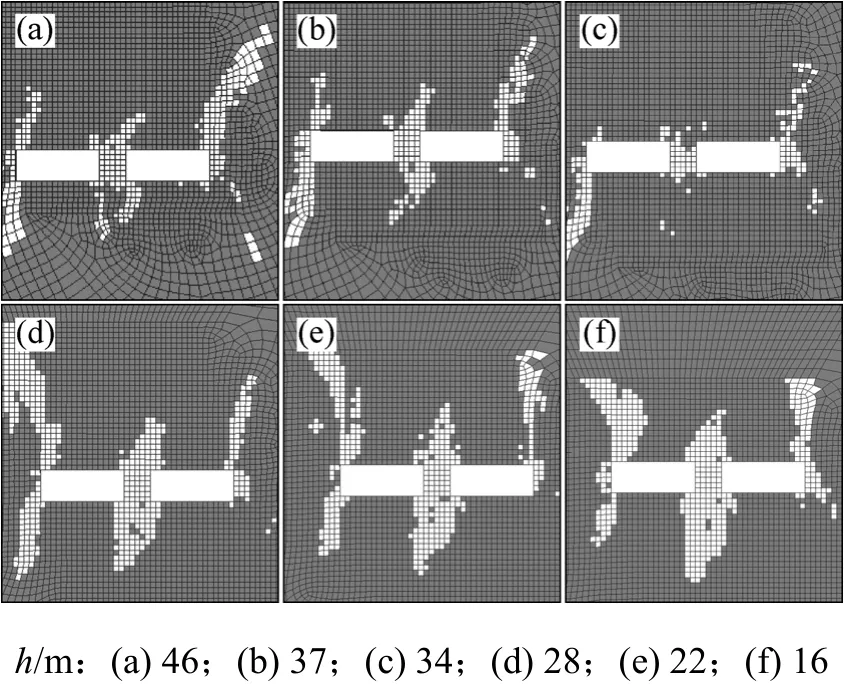
图4 d=5 m和D=16 m时围岩塑性变形区Fig.4 Rock’s plastic deformation zones when d=5 m and D=16 m

从图4可见：(1) h减小，空区底板端部塑性变形区逐渐减小，这是空区不断上移导致地应力逐渐减小造成的；(2) h减小，空区顶板两端及立柱上下端塑性变形区先减小后增大。对比图3和 4可发现：在 h=28 m时，围岩塑性变形区发生了跳跃性增大，之后主要增大的部位为立柱上下端，其他位置变化较小。由于开挖过程中主要关注空区顶板，故认为第2个规律是同跨度下围岩塑性变形的主要特征。

图5所示为h=19 m时不同跨度下围岩的塑性变形情况。从图5可以看出：跨度对围岩塑性变形的影响非常大，跨度减小，围岩各个部位的塑性变形区均显著减小。

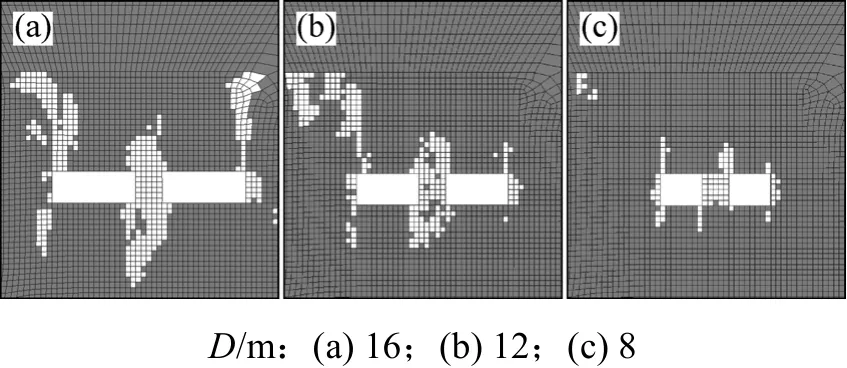
图5 h=19 m时不同跨度下围岩塑性变形区Fig.5 Rock’s plastic deformation zones under different spans when h=19 m

为便于表述，在此又定义：当立柱厚度为d=i m、空区跨度为D=j m时，在h不断减小过程中，围岩塑性变形区出现一次跳跃性增大，称此时空区的顶柱厚度为重要顶柱厚度，用 Hi,j表示。通过对各种跨度下围岩塑性变形区的观察和对比，可得如下顶柱厚度：H5,16=28 m，H5,14=25 m，H5,12=22 m，H5,10=19 m，H5,8=16 m。不难发现：重要顶柱厚度与关键顶柱厚度是相等的，下面统称为关键顶柱厚度，且仅通过位移来确定关键顶柱厚度。

可以认为：当空区顶柱厚度等于关键顶柱厚度时，露天坑底板压力开始对空区产生直接影响。所以，在关键顶柱厚度之后，空区越来越靠近露天坑底板，来自露天坑底板的压力越来越明显，导致空区顶板位移迅速增大。D越大，关键顶柱厚度越大，表明跨度增大，使空区在更大的顶柱厚度下便受到露天坑底板压力的直接影响。

3.1.3 空区破坏特征分析

从表2可以看出：当空区破坏时，空区顶板大幅度下沉，而立柱顶部下沉量却减小，说明空区破坏时立柱仍然稳固。图6所示为D=16 m，h为7 m和4 m时空区的破坏情况。

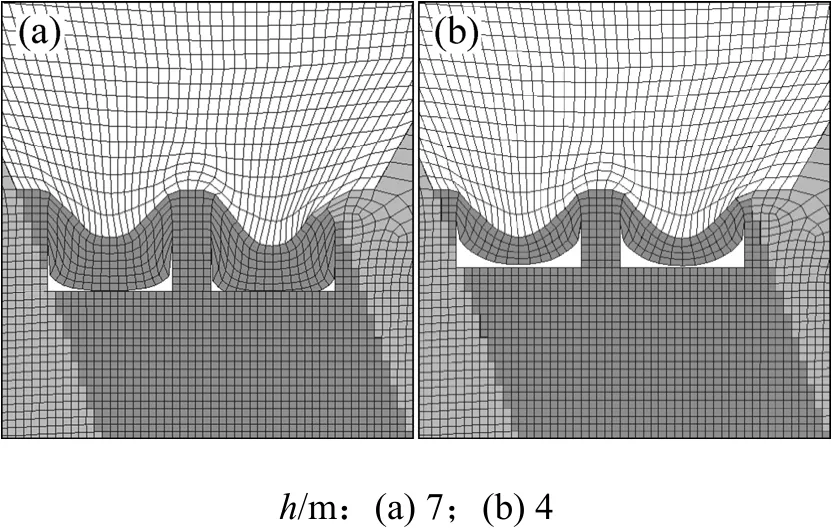
图6 d=5 m和D=16 m时空区破坏情况Fig.6 Goaf’s failure features when d=5 m and D=16 m

图7 所示为D=16 m和h=7 m时3号监测点水平应力随时间步的变化曲线。从图7可以看出：曲线未出现突变，而是逐渐收敛于某一值。曲线上拉应力峰值为0.778 3 MPa，未达到抗拉强度；1号监测点水平应力曲线(未贴出)也未出现突变，由此可判定空区破坏形式不是顶板受拉破坏。

图8所示为D=16 m和h=7 m时监测点4～7号剪切破坏阀值Fs随时间步的变化曲线。从图8可以看出：4个监测点的Fs都先后达到0，由此可判定空区破坏形式为顶板两端剪切破坏。据history命令记录的表格及曲线坐标，可知4个监测点的Fs达到0的时间步分别为：n(4号)=73 380，n(5号)=72 940，n(6号)=71 530，n(7号)=71 710，由此可知顶板端部发生剪切破坏的先后顺序监测点为6，7，5和4。

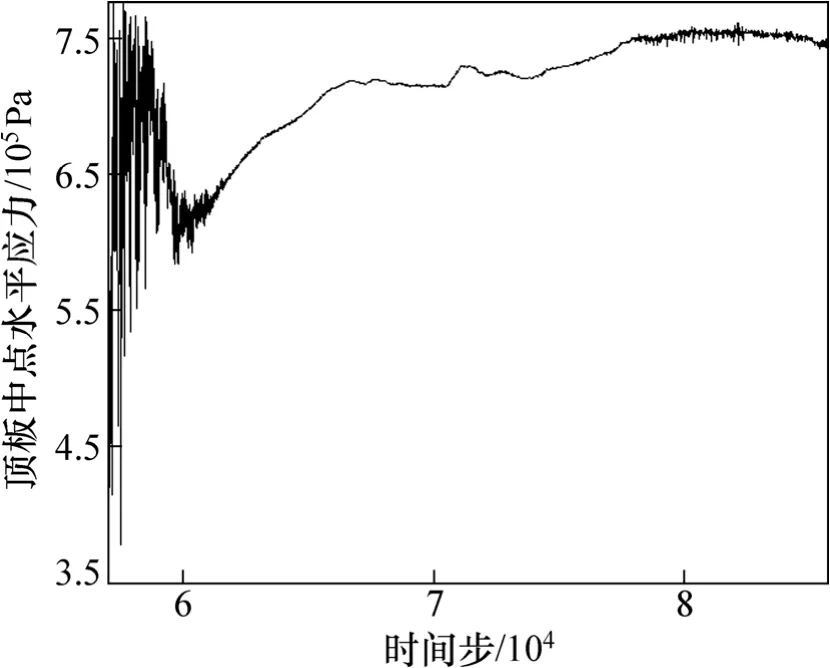
图7 D=16 m和h=7 m时3号监测点水平应力-时间步曲线Fig.7 Horizontal stress-step curve of 3# monitoring point when D=16 m and h=7 m

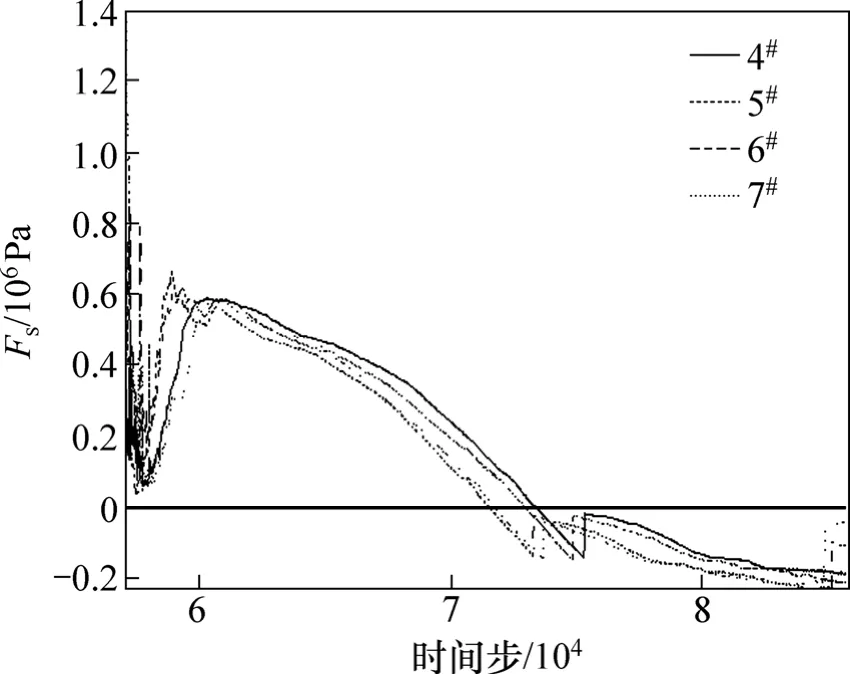
图8 D=16 m和h=7 m时监测点Fs-n曲线Fig.8 Fs-n curve of monitoring point when D=16 m and h=7 m

其他跨度的模拟结果表明：所有空区的破坏形式均为顶板两端剪切破坏。各监测点发生剪切破坏的时间步及发生破坏时的顶柱厚度如表3所示。

从表3可以看出：剪切破坏均先发生在立柱两侧的顶板端部上；横向对比采场跨度D为14，12和10 m时顶板端部发生剪切破坏的时间步。从表3可以看出：随着跨度的减小，空区顶板端部发生剪切破坏的时间越来越晚，说明空区跨度越小，空区稳定的时间越长。

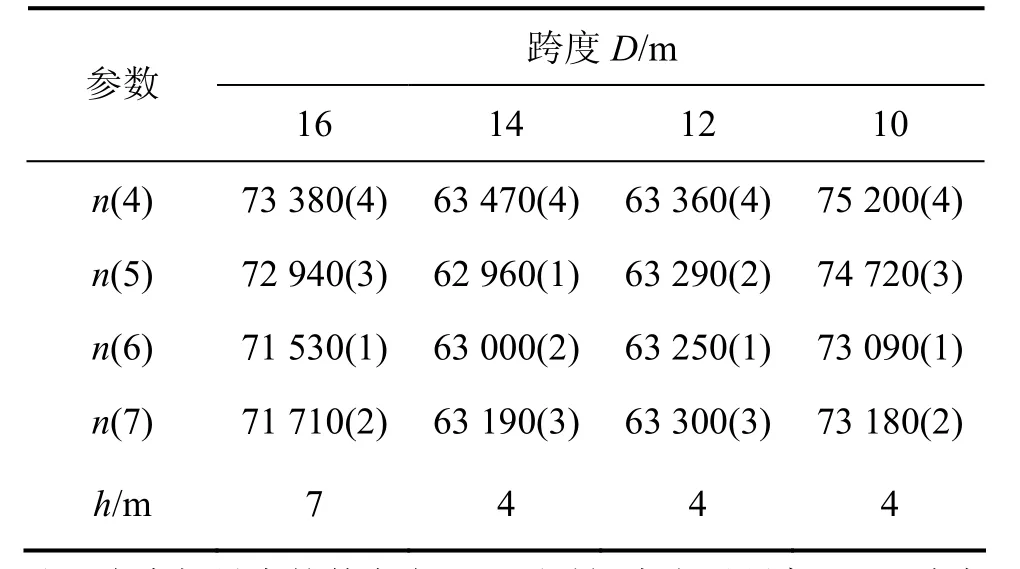
表3 不同跨度下各监测点发生剪切破坏的时间步Table 3 Nstep of monitoring points under different spans when goaf fails

3.2 采场跨度D一定但立柱厚度d不同时开挖模拟结

果及分析

下面以D=10 m为代表，分析不同立柱厚度下空区围岩的变形破坏特征。

3.2.1 监测点位移分析

表4所示为D=10 m时，不同立柱厚度下各监测点铅垂方向位移。从表4可以看出：立柱厚度减小，各监测点位移增大，h不断减小过程中，各监测点位移先减小后增大，不同立柱下的关键顶柱厚度为：h7,10=19 m，h6,10=19 m，h5,10=19 m，h4,10=22 m，h3,10=22 m，h2,10=25 m，说明立柱厚度d减小，使空区在更大的顶柱厚度下便开始受到露天坑底板压力的直接影响。

3.2.2 空区围岩塑性变形分析

图9所示为h=10 m时，各种立柱厚度下围岩塑性变形情况。从图9可以看出：立柱厚度减小，空区围岩各个部位的塑性变形区均显著增大。

3.2.3 空区破坏特征分析

对比d为7，6，5和4 m时空区破坏时各监测点的位移情况。D为7，6和5 m且空区破坏时2号监测点位移减小，说明空区顶板垮塌时立柱仍稳固；d=4 m且空区破坏时 2号监测点位移从 21.54 mm增加到112.7 mm。因此可认为：当d=4 m时，立柱破坏已经成为导致空区破坏的因素之一。

由表4可知：当D=10 m，h=7 m，d≥4m时空区均未破坏，d≤3 m时，空区发生破坏，观察监测点Fs，均未达到 0，说明是立柱的承载力不足导致了空区的垮塌。图10所示分别为d=3 m和2 m时空区的破坏情况。从图10可以看出：立柱两侧已经隆起。图10(b)中隆起程度较为明显。

3.3 模拟结果综合分析

由表4可见：当D=10 m时，在d为7，6和5 m这3种开挖方式中，编号相同的监测点位移在h=4～46 m过程中差别均非常小。由此可以认为：在立柱稳定的情况下，空区的变形及破坏规律仅与空区跨度相关，立柱厚度的变化对其影响较小；因此，以立柱厚度d=5 m为代表模拟各种跨度下的开挖过程，由其模拟结果得出的规律可以代表各种稳定的立柱厚度下的规律。

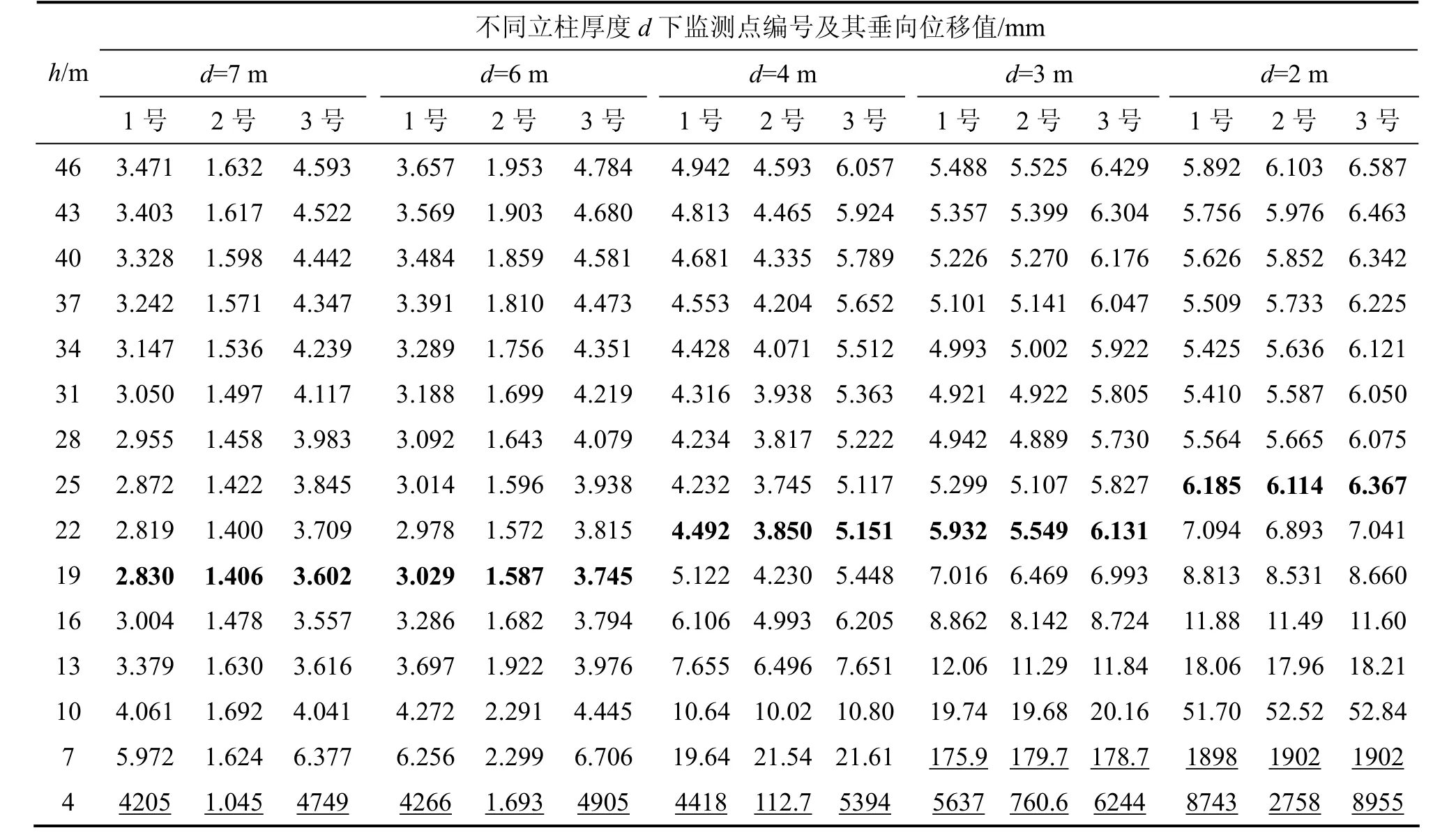
表4 D=10 m时不同立柱厚度下各监测点位移Table 4 Displacements of monitoring points under different column thicknesses when D=10 m

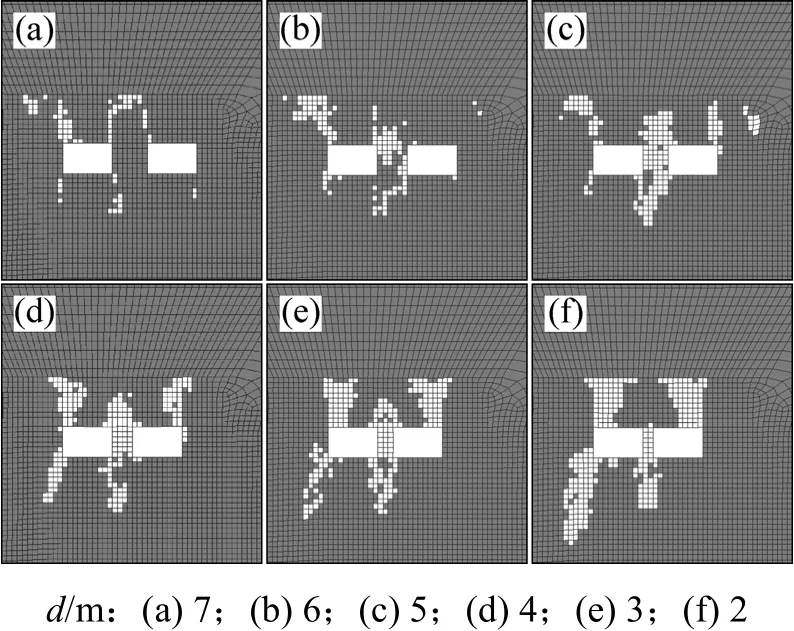
图9 h=10 m时不同立柱厚度下围岩塑性变形区Fig.9 Rock’s plastic deformation zones under different column thicknesses when h=10 m

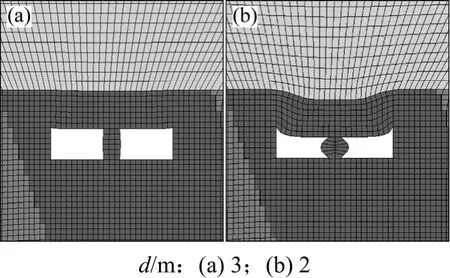
图10 h=7 m时不同立柱下空区破坏情况Fig.10 Goaf failure features under different columns when h=7 m

3.3.1 境界矿柱厚度的确定

从图4可以看出：当顶柱厚度h≤28 m时，围岩塑性变形区贯通露天坑底板(1号采场左上角位置)。对于本文研究的矿山，由于露天坑内积水较多，故境界矿柱应能够避免积水通过塑性区域的节理裂隙灌入采场(发生塑性变形说明岩体中节理裂隙已经扩展)。因此，当d=5 m和D=16 m时，应留31 m境界矿柱。按照同样方法，可定出各种开挖方式下应留的境界矿柱厚度(用K表示)，如表5所示。

从表5可以看出：在立柱稳定的情况下，境界矿柱厚度仅与空区跨度有关，且境界矿柱厚度和该种开挖方式的关键顶柱厚度基本一致。由此看出：为了地下采矿的安全，当采场围岩开始受到露天坑底板压力的直接影响时，应该停止采矿作业，用充填料对采空区进行回填，以免上部积水灌入采场。

3.3.2 空区跨度的确定

从表5可以看出：跨度越小，预留境界矿柱厚度越薄，由境界矿柱带来的矿量损失就越少。但是，并非跨度越小越好。因为采场宽度越小，应布置的采场数目越多，采场间的隔离矿柱(即立柱)越多，矿量损失也越大。而且在一般情况下，较小的采场不能进大型设备，导致采矿效率低下，采矿时间延长，作业安全性降低。因此，应该找到跨度与矿量损失及采矿效率的平衡点。参照文献[10]，大量国内外露天转地下开采的矿山，境界矿柱常留约20 m。对于本文研究的矿山，根据矿山生产技术设备特点，可选采场宽度10 m，按表5可留19 m境界矿柱。3.3.3 最优立柱厚度的确定

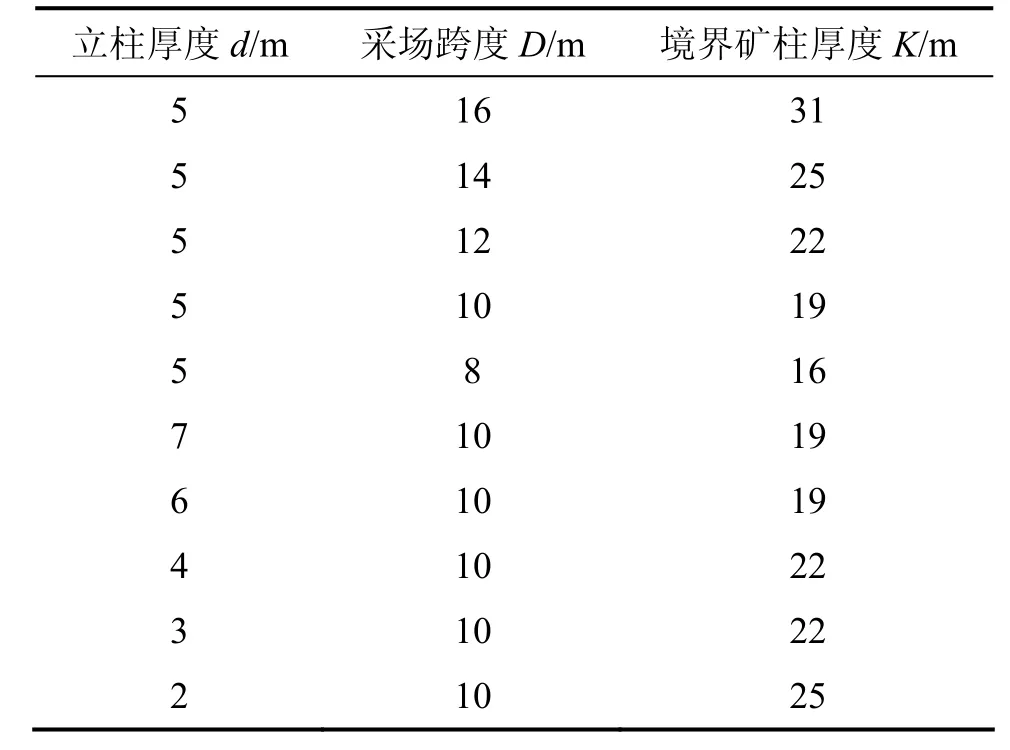
表5 各种开挖方式下应留的境界矿柱厚度KTable 5 Boundary pillar width K under different excavating forms

图11所示为h=7 m，D=10 m和d=7～2 m时空区围岩铅垂向位移云图。由图11可见：

(1) d由7 m转变为6 m时，主要沉降区移动较小，最大沉降部位仍位于空区顶板上，各监测点位移增大值约1 mm。

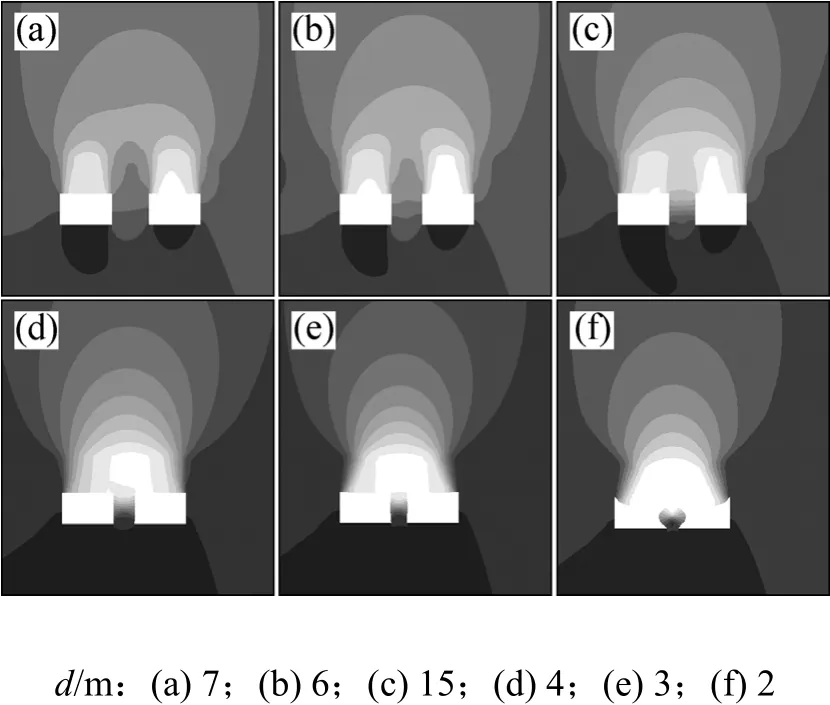
图11 D=10 m时不同立柱厚度下围岩位移云图Fig.11 Rock’s displacement nephograms under different column thicknesses when D=10 m

(2) d由6 m变为5 m时，主要沉降区移动较小，最大沉降部位仍在空区顶板上，各监测点的下沉量增大 1～3 mm。

(3) d由5 m变为4 m时，两采场的主要沉降区已经合并到立柱上方，各监测点位移增大 12～16 mm，且立柱顶部的位移增量最大。

可见：d从7 m变为6 m及从6 m变为5 m时，对空区影响较小；d从5 m变为4 m时对空区影响较大，可以认为发生了质变。从图9可知：当d≤5 m时，立柱内部各单元体均发生了塑性变形，说明立柱内部各个单元体均发挥了最大的支撑作用；而d为6 m和7 m时，立柱内部均有部分单元体未发生塑性变形。

由以上分析可以确定：d＜5 m时，则立柱承载力不足；d＞5 m时，造成不必要的矿柱矿量损失。因此，应保留立柱厚度d为5 m。

4 结论

(1) 在空区上移过程中，空区顶板位移及围岩塑性变形区均先减小后增大。

(2) 立柱稳固时，露天坑底板压力开始对空区产生直接影响的顶柱厚度h范围为19～28 m；立柱稳固时，空区顶板位移及围岩塑性变形区变化规律仅与空区跨度有关，立柱厚度的变化对其影响较小；立柱不稳固时，立柱厚度开始产生较大影响，跨度增大或立柱变薄，可使位移及塑性变形区显著增大，并使空区在更大的顶柱厚度下便受到了露天坑底板压力的直接影响。

(3) 立柱稳固时，空区破坏形式均为顶板两端剪切破坏，且靠近立柱的端部最先破坏；当跨度D=10 m，立柱厚度d≤4 m时立柱开始不稳固，空区破坏形式逐渐转向立柱破坏。

(4) 综合考虑矿山实际情况，推荐采场跨度D为10 m，立柱厚度d为5 m、境界矿柱厚度h为19 m。

本研究结果仅从定性上总结空区围岩的变形规律，要构建空区围岩位移与空区跨度、顶柱厚度及立柱厚度等相关影响因素的函数关系，从定量上说明变形规律，还需进一步研究。

[1] 南世卿, 赵兴东. 断层影响下境界矿柱稳定性数值分析[J].金属矿山, 2005(3): 28-30.NAN Shi-qing, ZHAO Xing-dong. Instability numerical analysis of boundary pillar affected by fault[J]. Metal Mine, 2005(3):28-30.

[2] 韩现民, 李占金, 甘德清, 等. 露天转地下矿山边坡稳定性数值模拟与敏感度分析[J]. 金属矿山, 2007(6): 8-12.HAN Xian-min, LI Zhan-jin, GAN De-qing, et al. Numerical simulation and sensitivity analysis of slope stability in mine transferred from open-pit to underground mining[J]. Metal Mine,2007(6): 8-12.

[3] 田泽军, 南世卿, 宋爱东. 露天转地下开采前期关键技术措施研究[J]. 金属矿山, 2008(7): 27-29.TIAN Ze-jun, NAN Shi-qing, SONG Ai-dong. Key technical measures in the early period of transition from open-pit to underground mining[J]. Metal Mine, 2008(7): 27-29.

[4] 闫长斌, 徐国元, 李夕兵. 爆破震动对采空区稳定性影响的FLAC3D分析[J]. 岩石力学与工程学报, 2005, 24(16):2894-2899.YAN Chang-bin, XU Guo-yuan, LI Xi-bing. Stability analysis of mined-out areas influenced by blasting vibration with FLAC3D[J].Chinese Journal of Geotechnical Engineering, 2005, 24(16):2894-2899.

[5] Itasca Consulting Group Inc. FLAC3D(Fast Lagrangian Analysis of Continua in 3 Dimensions)Version 3.1, Users Guide[M].USA：Itasca Consulting Group Inc, 2006: 1-127.

[6] 何忠明, 曹平. 考虑应变软化的地下采场开挖变形稳定性分析[J]. 中南大学学报: 自然科学版, 2008, 39(4): 641-646.HE Zhong-ming, CAO Ping. Deformation and stability analysis of underground stope after excavation considering strain softening[J]. Journal of Central South University: Science and Technology, 2008, 39(4): 641-646.

[7] 谢和平, 周宏伟, 王金安, 等. FLAC在煤矿开采沉陷预测中的应用及对比分析[J]. 岩石力学与工程学报, 1999, 18(4):397-401.XIE He-ping, ZHOU Hong-wei, WANG Jin-an, et al.Application and contrastive analysis of FLAC in forecasting coal mining subsidence[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(4): 397-401.

[8] 余学义, 尹士献, 赵兵朝. 采动厚湿陷性黄土破坏数值模拟研究[J]. 西安科技大学学报, 2005, 25(2): 135-138.YU Xue-yi, YIN Shi-xian, ZHAO Bing-chao. Numerical simulation about the damage of thick collapsible loess by mining[J]. Journal of Xi’an University of Science and Technology, 2005, 25(2): 135-138.

[9] 王文星. 岩体力学[M]. 长沙: 中南大学出版社, 2004:184-185.WANG Wen-xing. Rock mechanics[M]. Changsha: Central South University Press, 2004: 184-185.

[10] 陈文林, 张永彬, 杨天鸿, 等. 露天转地下境界矿柱稳定性评价[J]. 地下空间, 2004, 24(2): 260-264.CHEN Wen-lin, ZHANG Yong-bin, YANG Tian-hong, et al.Stability judging for boundary pillar of underground mining shifted from open-pit[J]. Underground Space, 2004, 24(2):260-264.