充填环境下预裂缝的爆破动力响应分析

胡建华，雷涛，周科平，陈庆发

(中南大学 资源与安全工程学院，湖南省深部金属矿开发与灾害控制重点实验室，湖南 长沙，410083)

在矿山生产中，常采用预裂爆破来控制爆破对围岩及其周边环境的损伤。目前，国内外研究人员主要从理论分析和数值模拟的角度对预裂缝作用机理及其降振效果进行研究。由于预裂爆破降振机理的研究涉及波动理论、岩体力学以及地震学等诸多学科，因此，要完全从理论上解决预裂缝减振问题非常困难[1-2]。李夕兵等[3-4]采用库仑摩擦定律描述界面强度的方法研究了岩体软弱结构面对应力波传播的影响。Myer等[5-6]采用节理刚度描述的界面模型研究了爆炸应力波与预裂缝的相互作用。王明洋等[7]提出计算爆炸地震波通过削弱层的简化模型，运用黏弹性波动理论，得到爆炸地震波通过断裂构造的衰减公式。在实际工程中，岩体并非理想的弹性介质，在爆破动力载荷作用下，岩体通常表现出较强的弹塑性和黏弹性。实际上，应力波在传播过程中，由于内摩擦的作用而必然导致能量耗散，同时，预裂缝两边介质性质不同将会导致在交界面上产生应力集中现象，在缝岸附近，由于几何不连续，材料不连续，其位移和应力呈现出极其复杂的状态[8]，因而，要得出爆炸应力波与预裂缝间的相互作用的解析解非常困难。一些研究者通过数值模拟开展了对预裂缝的研究，并用数值模拟结果指导实践，取得了很好的效果，如：Chen等[9]利用数值分析的方法在分析地下球状药包爆炸的基础上研究了节理岩体的振动特征；梁开水等[10-12]利用LS-DYNA动力分析软件模拟了在露天矿生产中，不同宽度、长度和深度的预裂缝的降振效果，模拟结果和史秀志等[13]在大冶露天矿实际检测的结果基本一致。但上述对预裂缝作用机理的研究主要集中在露天条件下，而在地下环境中，由于工程条件往往与露天的差别很大，预裂缝对爆破动载荷的响应有很大不同。目前，对地下采矿特别是采矿环境再造条件下，通过形成人工矿柱回采矿体，利用预裂缝对爆破扰动作用和矿柱回采夹制作用的控制等的研究相当少。在此，本文作者以华锡集团高峰矿碎裂矿段开采研究为基础，根据现场岩石力学特性和装药，用高能炸药的状态方程模拟炸药的爆炸过程，采用有限元动力分析软件ANSYS/LS-DYNA模拟地下开采环境下邻近充填体的预裂缝的作用机理。

1 数值计算模型

1.1 工程背景

高峰矿是华锡集团控股的大型矿山基地之一。在大厂矿区国家规划区的2.8 km2范围内，有2个国内外罕见的特富多金属矿体，即100号和105号矿体，其潜在的价值近200亿元。由于多年来非法民采形成大量的未经处理的空区，使矿体的完整性受到破坏，极大地扰动和破坏了矿岩体原有稳定状态，形成了具有大面积的碎裂矿岩体的灾害隐患矿床。采用充填采矿法对高峰矿进行开采。由于在某些区域，条柱的宽度仅为4 m，为了保证相邻的充填体的安全，需要在近充填体的矿体中进行预裂爆破。

1.2 模型构建

数值模型如图1所示。根据高峰矿的实际情况，作如下简化和假定：

(1) 模型尺寸为6 m×2 m×10 m。

(2) 预裂缝为一长方体裂隙，其间为空气夹层。预裂缝长度为7.5 m，宽度为0.1 m。

(3) 在不影响模拟结果的条件下，简化原扇形装药为药包集中装药。

为开展对比分析研究，数值模拟3种工况。工况1：所有的介质材料均为矿体，既没有预裂缝，也没有分界面；工况2：在工况1的基础上加上矿体和充填体之间的分界面；工况 3：见图 1(b)，反映的是实际情况，既有预裂缝，也有分界面。

模拟采用 ALE算法进行计算，计算终止时间为4 000 μs。设定模型的左表面为约束边界，下表面为自由边界，其余面为无反射边界。

图1 数值计算几何模型Fig.1 Numerical geometric model

1.3 材料模型及状态方程

矿体和充填体均采用弹塑性模型。该模型使用弹性和塑性2种斜率来表示材料应力应变行为。实测的矿体和充填体的力学参数见表1。

炸药模型采用高能炸药材料模型。炸药爆炸后，任意时刻内爆源内的压力[14-15]可表示为：

式中：p为爆炸压力，Pa，；F为炸药的化学能释放率；D为炸药爆速，m/s；t和t1分别为当前时间和炸药内一点的起爆时间，s；Aemax为炸药单元横截面积最大值；ve为炸药单元体积；peos为由 Jones-Wilkins-Lee(JWL)状态方程决定的压力，Pa；E为单位体积比内能，Pa；A，B，R1，R2，ω均为与炸药相关的材料系数；V为相对体积；E0为初始比内能，Pa。

高峰矿采用的是2号岩石硝铵炸药，炸药参数和JWL状态方程参数见表2。

空气材料采用空白材料模型。其状态方程为

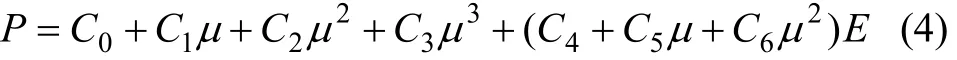
表1 矿体和充填体物理力学参数Table 1 Mechanical properties of orebody and backfill

表2 炸药和状态方程参数Table 2 Properties of explosive and JWL equations

2 数值计算结果及分析

2.1 应力波传播的分析

炸药起爆后，应力波从爆源向外传播，在应力波传至预裂缝前，预裂缝和分界面的作用尚未表现。在1.0 ms左右，应力波传到预裂缝，开始有反射现象产生；在1.5 ms左右，预裂缝显示出对应力波很强的反射效应并出现反射波和入射波的叠加，同时，分界面对应力波的反射、衍射效应也开始体现；在2 ms左右，应力波在反射叠加的基础上，出现了绕射，并且有无分界面的应力波的传播出现了较大的差异，通过分界面的应力波强度明显减小；在2.5 ms左右，应力波的传播受到预裂缝和分界面的影响，其经过反射后的叠加效应表现得非常明显，在靠近爆源的一侧，应力波明显加强。对比的模拟结果如图2所示。

2.2 典型爆破振动波形图

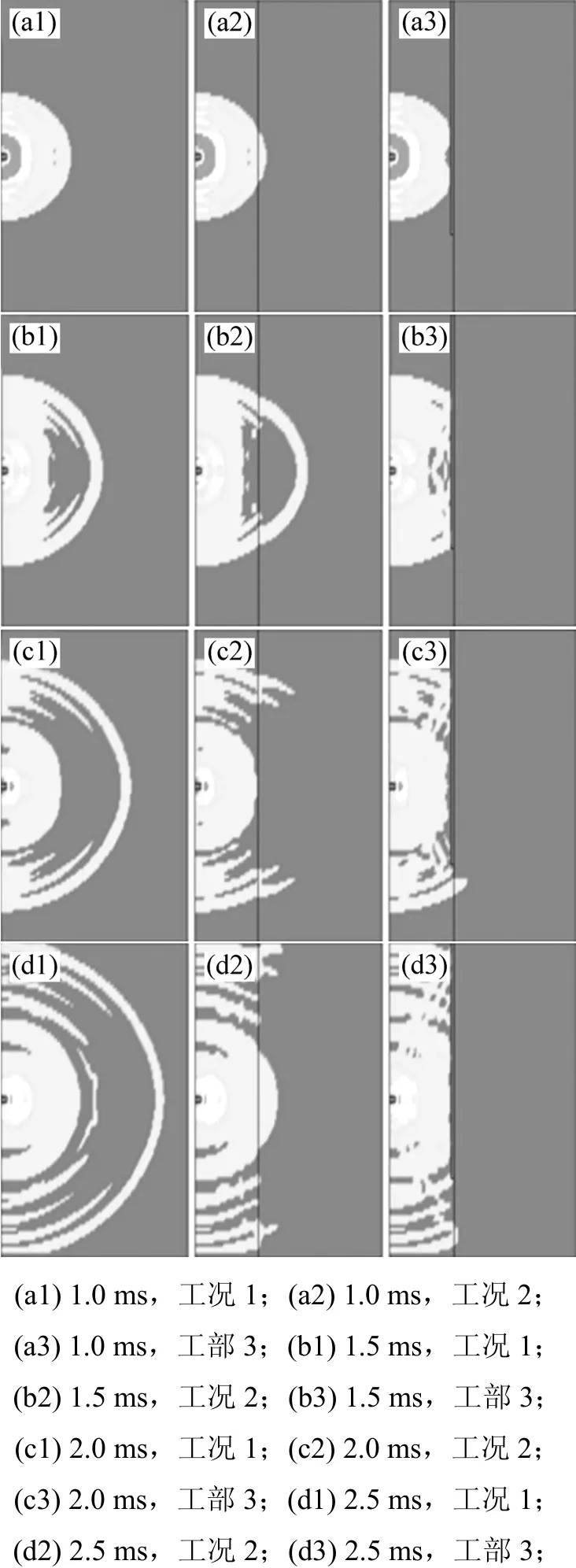
图2 3种工况下Von Mises应力云图Fig.2 Von Mises stress contours of three options

利用LS-DYNA的后处理功能，可得到质点的速度-时间曲线，如图3所示。取测线上预裂缝前0.2 m(距爆源1.8 m，曲线A)处和缝后0.4 m(距爆源2.4 m，曲线B)处的2个质点，分别绘出3种工况下的速度-时间曲线，以此表示典型的爆破振动波形图。

由图3可知：工况1的2条曲线有着相似的变化规律；工况2的曲线在2.5 ms后表现出较大的差异，反映了分界面对爆炸应力波传播的影响；工况3的2条曲线表现出很大差异，充分体现了预裂缝对爆炸应力波的阻隔效应。

2.3 质点振动速度的分析

沿垂直于预裂缝与炸药中心等高的测线取质点振动速度峰值，得到图4和图5所示曲线。计算值的曲线由萨道夫斯基公式[16]计算所得：

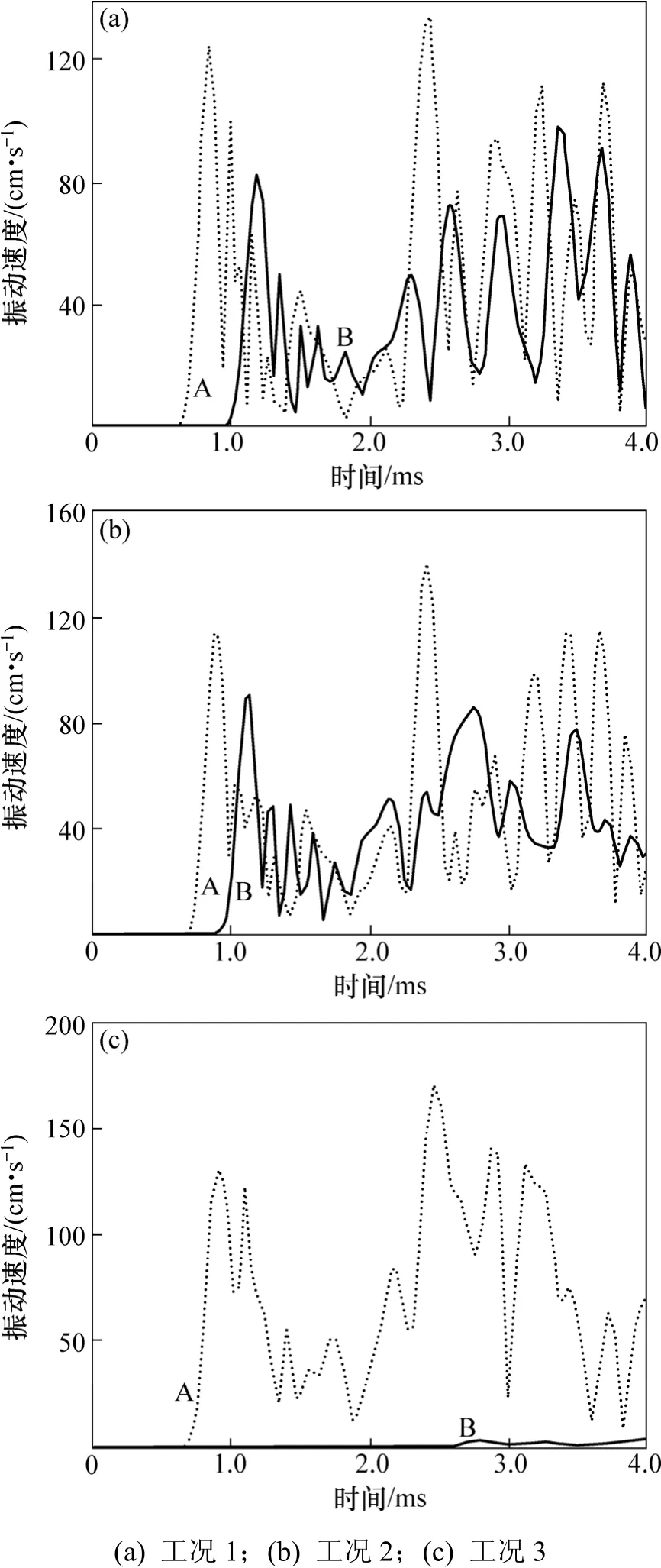
图3 3种工况下质点的v-t曲线Fig.3 Particle’s v-t curves of three options

式中：v为质点振动速度最大值，cm/s，；Q为装药量，kg；R为测点至爆源的距离，m；K和α为爆破现场的特征系数，分别取80.0和1.3。

由图4和图5可知：预裂缝前、后的质点振动速度具有相同的衰减规律。使用萨道夫斯基公式计算的质点振动速度峰值比数值模拟的要大。这是因为在使用萨道夫斯基公式时，需要根据不同的场地条件对K和α进行选取，由此导致这种差异。

图4 预裂缝前速度峰值Fig.4 Peak velocity of before pre-splitting crack

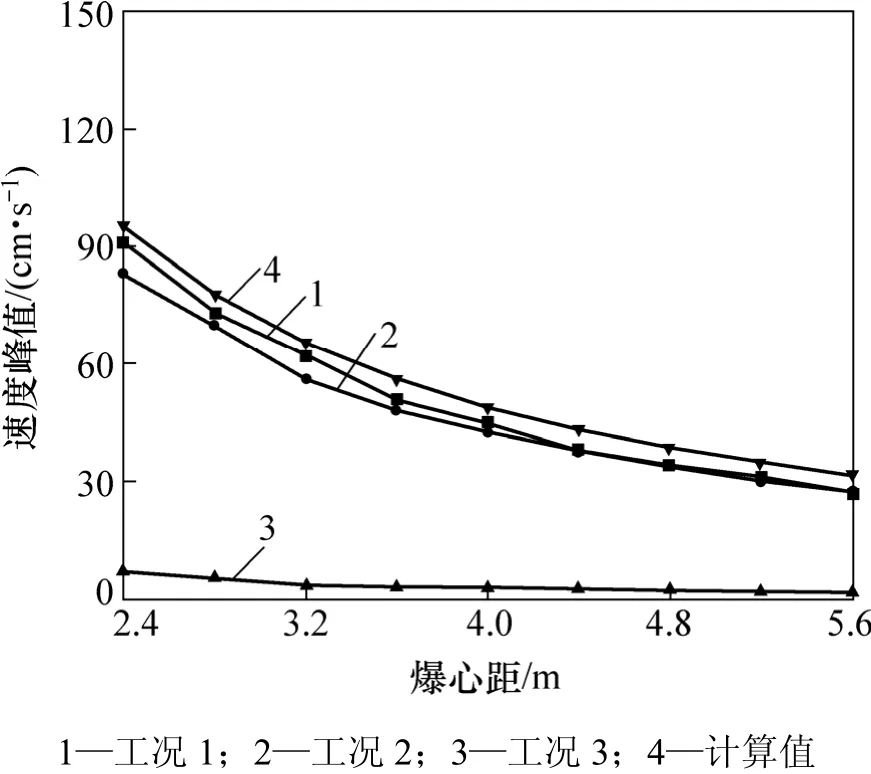
图5 预裂缝后速度峰值Fig.5 Peak velocity of after pre-splitting crack

预裂缝后的质点振动速度大大降低。对比图4和图5可知：在预裂缝后，质点振动的速度出现了很大的衰减，质点振动速度峰值从爆心距为1.8 m时的130 cm/s降至2.4 m时的4.8 cm/s，表明预裂缝具有很好的降振效果。

在图5中，有分界面时的质点振动速度峰值也比无分界面时的值要小，这说明2种不同介质之间的自然分界面具有一定的降振效应。

3 作用机理

3.1 预裂缝降振效应

经过预裂缝后，由于应力波的发射、绕射和透射，使得爆炸能量急剧衰减，预裂缝后的质点振动速度急剧降低。以公式(6)表示预裂缝的降振率，可绘出预裂缝降振率的曲线如图6所示。

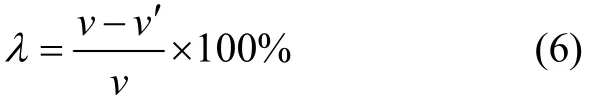
式中：v表示无预裂缝无分界面时的质点振动速度峰值，v′表示有预裂缝或分界面时的质点振动速度峰值。

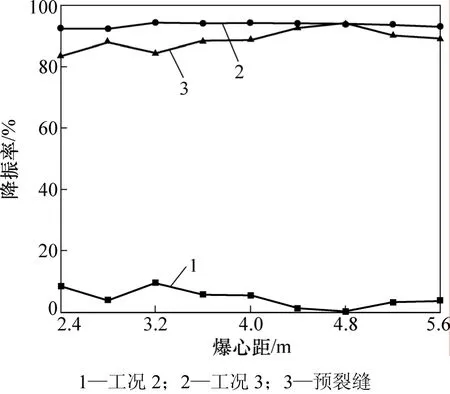
图6 降振率曲线Fig.6 Damping ratio curves

由图 6可知：分界面的降振率基本上处在3%～10%之间，表明在一定程度上，矿体和充填体的界限也可当成较窄的预裂缝来处理。

从图6可见：预裂缝的降振率在80%～90%之间，最大达到了94%，具有良好的降振率，控制了爆破对充填体的扰动；降振率曲线 2(工况 3)的取值在92%～94%之间。这主要是由于矿体和充填体分属不同的介质，爆炸应力波在经过预裂缝传到充填体时，发生了2次反射，进一步加强了了预裂缝的降振效应。数值模拟得到的降振率比通常实际的预裂缝的降振率偏大，其主要原因有：

(1) 由于爆源距预裂缝较近，在实际中形成的预裂缝有可能在强应力波作用下产生闭合，影响了预裂缝的降振效果。

(2) 在实际情况中，岩体在预裂爆破时不太可能形成如数值模拟那样状况良好的预裂缝，导致预裂缝的宽度达不到理想宽度，在局部地区还可能出现两边介质相连的现象，或者预裂缝被某些介质充填，从而不能形成1条完全分开的缝隙，这就大大降低了预裂缝的降振效果。

(3) 若实际中预裂缝若未达到一定的长度，则爆破地震波就可能比较容易地绕过预裂缝，也会降低预裂缝的降振效果。

图5表明：由于应力波的反射、折射等作用，预裂缝降振率最好的区域不在距预裂缝最近的区域，而在距预裂缝2～4 m的区域。

3.2 预裂缝能量聚集效应

由图4可知：在爆心距为1.2 m之前，预裂缝对质点振动速度峰值几乎没有影响，3种工况的质点振动速度峰值曲线完全重合，但在预裂缝前的1 m以内(爆心距1.2～2.0 m)，有预裂缝的质点振动速度峰值要比无预裂缝的偏大，表明预裂缝对爆炸能量在矿体内产生了聚集效应。用预裂缝的能量聚集率类推降振率η的定义可以式(7)表示，能量聚集率曲线如图7所示。

图7中，在距预裂缝0.6 m(即爆心距1.4 m)处，开始表现出较明显的能量聚集效应，且距预裂缝越近，聚集效应越明显，预裂缝的最大聚集率达到25%左右。这是由于应力波经过预裂缝的反射后发生了相互叠加，使得在邻近爆源的一侧应力加强。预裂缝的这种能量聚集效应有效弱化了矿柱回采的夹制作用，有利于矿石的破碎，降低大块率。

图7 能量聚集率曲线Fig.7 Curves of gathering ratio

4 结论

(1) 预裂缝具有良好的降振效果，爆炸应力波在经过预裂缝时急剧衰减，降振率可达到80%～90%。

(2) 不同介质的自然分界面为弱结构面，爆炸应力波在经过分界面时会发生与预裂缝相似的反射、绕射和透射现象。

(3) 预裂缝表现出较强的能量聚集效应。在邻近爆源的一侧，爆炸应力加强，且这种响应强度随爆心距的增大而加强。

(4) 为充分发挥预裂缝的作用，预裂缝的长度应大于被保护区的长度，以阻隔应力波从缝底绕射进入被保护区，宽度应保证在爆破应力波作用下不会闭合。

[1] 凌同华, 李夕兵. 爆破振动信号不同频带的能量分布规律[J].中南大学学报: 自然科学版, 2004, 35(2): 310-315.LING Tong-hua, LI Xi-bing. Laws of energy distribution in different frequency bands for blast vibration signals [J]. Journal of Central South University: Science and Technology, 2004,35(2): 310-315.

[2] 鞠杨, 环小丰, 宋振铎, 等. 损伤围岩中爆炸应力波动的数值模拟[J]. 爆炸与冲击, 2007, 27(2): 136-142.JU Yang, HUAN Xiao- feng, SONG Zhen-duo, et al. Numerical analyses of blast wave stress propagation and damage evolution in rock masses[J]. Explosion and Shock Waves, 2007, 27(2):136-142.

[3] 李夕兵. 论岩体软弱结构面对应力波传播的影响[J]. 爆炸与冲击, 1993, 13(4): 334-342.LI Xi-bing. Influence of the structural weakness planes in rock mass on propagation of stress waves[J]. Explosion and Shock Waves, 1993, 13(4): 334-342.

[4] 王卫华, 李夕兵, 周子龙, 等. 不同应力波在张开节理处的能量传递规律[J]. 中南大学学报: 自然科学版, 2006, 37(2):376-380.WANG Wei-hua, LI Xi-bing, ZHOU Zi-long, et al.Energy-transmitted rule of various stress w aves across open joint[J]. Journal of Central South University: Science and Technology, 2006, 37(2): 376-380.

[5] Myer L R. Effects of Single Fracture on Seismic Wave Propagation[C]//Barton & Stephansson, eds Rock Joints.Rotterdam: Bakema, 1990: 467-473.

[6] 卢文波, 赖世骧, 董振华. 岩石钻爆开挖中预裂缝的隔震效果分析[J]. 爆炸与冲击, 1997, 17(3): 193-198.LU Wen-bo, LAI Shi-xiang, DONG Zhen-hua. Analysis of vibration isolating effect of pre-splitting crack in rock excavation by blasting[J]. Explosion and Shock Waves, 1997, 17(3):193-198.

[7] 王明洋, 唐廷, 周泽平. 断裂构造对爆炸地震波传播规律的影响[J]. 岩石力学与工程学报, 2005, 24(增1): 4635-4641.WANG Ming-yang, TANG Ting, ZHOU Ze-ping. Effects of geogical structural faults on blasting seismic wave propagation[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Supp.1): 4635-4641.

[8] 梁岗, 贺鹏飞. 粘弹性双材料界面裂缝的缝端位移场及动态断裂分析[J]. 力学季刊, 2007, 28(1): 34-40.LIANG Gang, HE Peng-fei. The viscoelastic bi-materials interfacial displacement fields in crack tip vicinity and dynamic fracture analysis[J]. Chinese Quarterly of Mechanics, 2007,28(1): 34-40.

[9] Chen S G, Zhao J, Zhou Y X. UDEC modeling of a field explosion test[J]. International Journal of Blasting and Fragmentation, 2000(4): 149-163.

[10] 梁开水, 陈天珠, 易长平. 减震沟减震效果的数值模拟研究[J]. 爆破, 2006, 23(3): 18-21.LIANG Kai-shui, CHEN Tian-zhu, YI Chang-ping. Numerical simulation for vibration-isolating effect of vibration-isolating slot[J]. Blasting, 2006, 23(3): 18-21.

[11] 易长平, 陈明, 卢文波, 等. 减震沟减震的数值模拟[J]. 武汉大学学报, 2005, 38(1): 49-51.YI Chang-ping, CHEN Ming, LU Wen-bo, et al. Numerical simulation for damping effect of damping ditch[J]. Engineering Journal of Wuhan University, 2005, 38(1): 49-51.

[12] 罗毓, 刘雁鹰, 易长平. 预裂缝参数对减振效果影响的数值分析[J]. 爆破, 2007, 24(2): 25-35.LUO Yu, LIU Yan-ying, YI Chang-ping. Numerical simulation analysis of the effect of pre-splitting crack parameters on damping vibration[J]. Blasting, 2007, 24(2): 25-35.

[13] 史秀志. 爆破振动信号时频分析与爆破振动特征参量和危害预测研究[D]. 长沙: 中南大学资源与安全工程学院, 2007:62-63.SHI Xiou-zhi. Study of time and frequency analysis of blasting vibration signal and the prediction of blasting vibration characteristic parameters and damage[D]. Changsha: Central South University, School of Resources and Safety Engineering,2007: 62-63.

[14] Korichi T, Bachir B. Design of a model blasting system to measure peak P-wave stress[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(4): 513-519.

[15] Livermore Software Technology Corporation. LS-DYNA theoretical manual[R]. Utah: Livermore Software Technology Corporation, 1998: 610-611.

[16] 张雪亮, 黄树棠. 爆破地震效应[M]. 北京: 地震出版社, 1981:104-106.ZHANG Xue-liang, HUANG Shu-tang. Effect of blasting ground vibration[M]. Beijing: Earthquake Publishing House,1981: 104-106.