随机利率下的n年家庭收入保险

蔡井伟

（江苏农林职业技术学院基础部，江苏镇江 212400）

常规的年金都是以人的生存为给付条件，按预先约定金额进行一系列给付的寿险保障问题所采用的利率是确定的利率由于现实的利率和人的生命都是随机的（双随机），所以有必要在随机的利率、随机的死亡率假设下来研究年金问题，随机利率下年金的研究已经越来越成为精算领域的重要课题［1－4］，这些成果都以离散型为研究对象谢杰华研究了随机利率下的连续型生存年金［5］，但这种年金是以人的生存为给付条件的此处突破以人的生存为给付条件的限制，在双随机模型下研究了n年家庭收入保险，给出了n年家庭收入保险现值的期望值，并且在3种特殊的死亡假设下给出了现值期望值的具体表达式。

1 随机利率下n年家庭收入保险的现值

n年家庭收入保险是指当被保险人在n年内死亡时开始提供年金给付，直至第n年的一种特殊年金假设连续给付年支付额为1，则n年家庭收入保险的现值Y为:

2 n年家庭收入保险现值的期望值

对利息力累积函数采用wiener过程建模，即假设:

其中δ是常数利息力，σ是常数，σ≥0，Wt是标准的wiener过程，WtN（0，t）

研究n年家庭收入保险，得到了连续支付给付额为1的n年家庭收入保险现值的期望值。

定理1 利息力累积函数采用wiener过程建模，即设y（t）=δt+σWt，其中δ为常数利息力，σ是常数，σ≥0，那么对于连续支付给付额为1的n年家庭收入保险的现值Y的期望值有表达式:

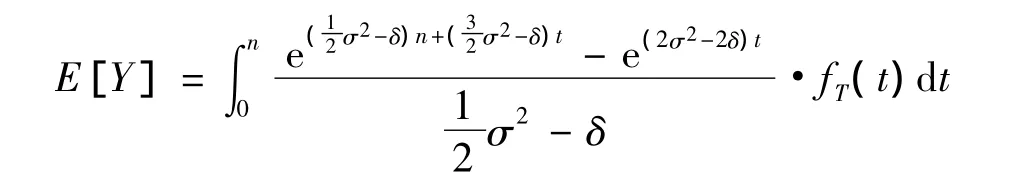
证明 由于y（t）独立于T（x），因此，有条件概率:

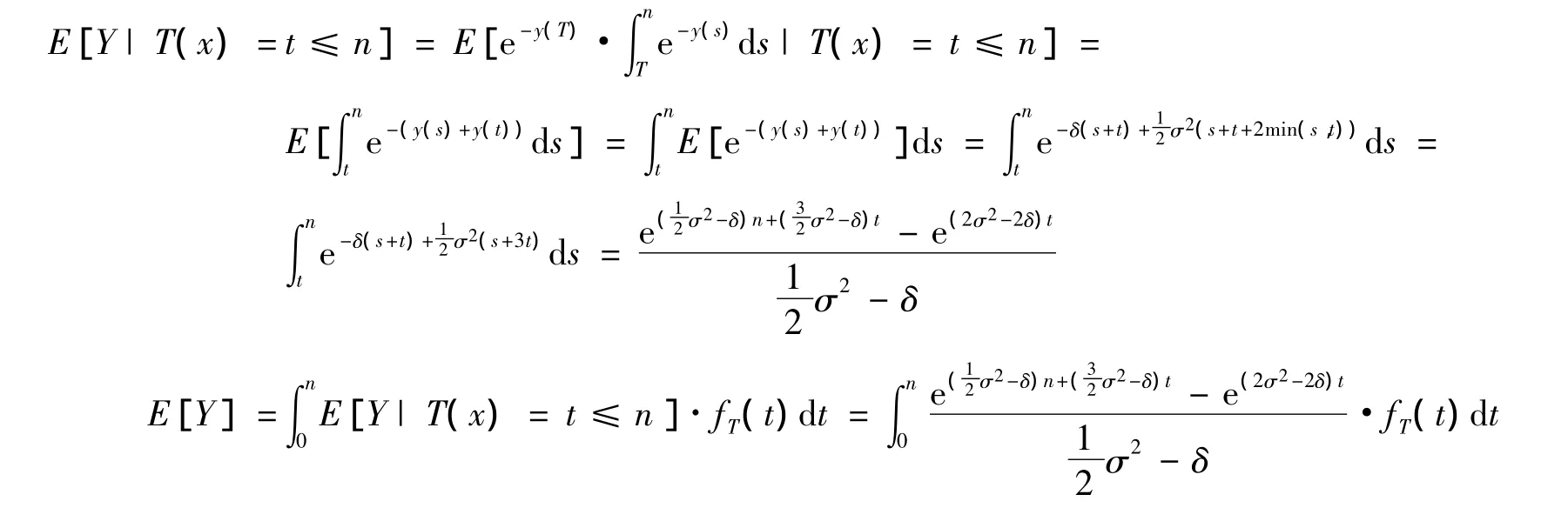
3 特殊死亡假设下现值期望值的表达式

在精算学3种常见的死亡精算假设下，给出上述定理的具体表达式:

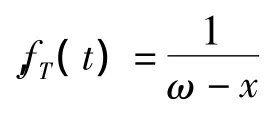
（2）假设死亡满足指数分布假设，假定fT（t）=λe－λt，其中t∈［0，∞），λ ＞0，有:

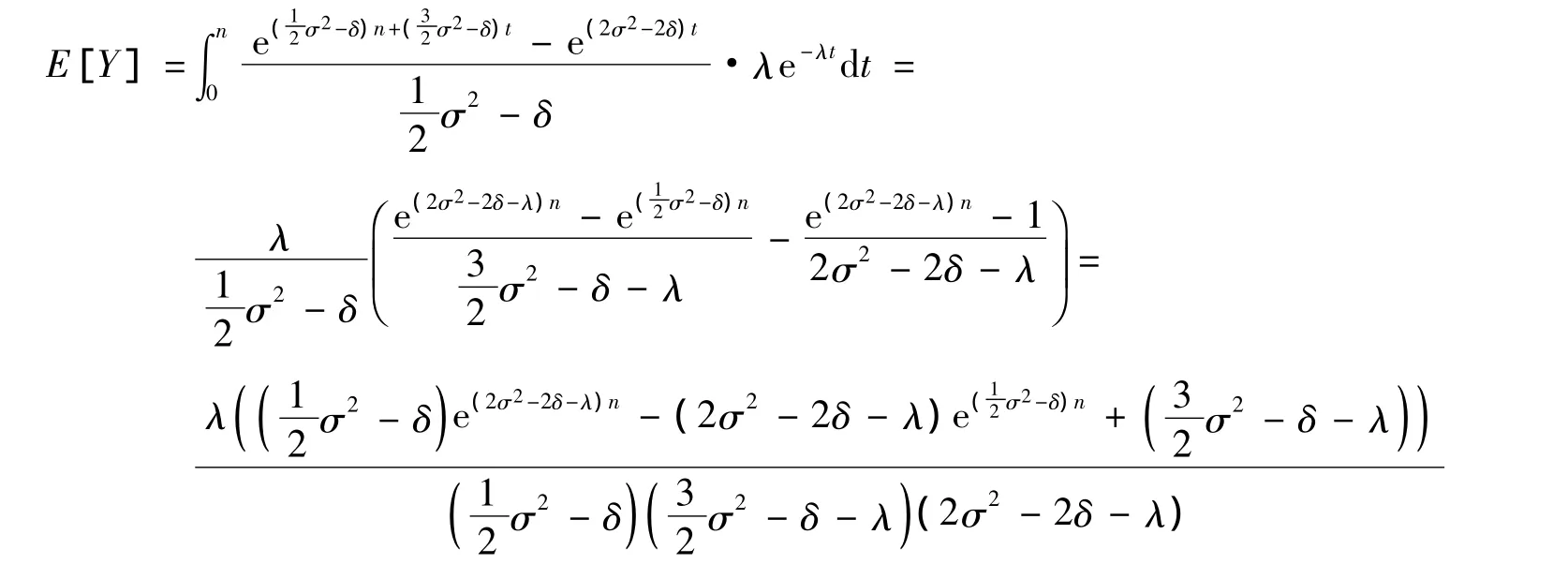
4 结语

在寿险业实际使用的保险业务上建立模型，对其进行研究具有很现实的意义。可为寿险精算师对该业务的定价、责任准备金的计算等提供理论、技术上的支持。有了现代计算机强大的计算功能，计算特殊死亡假设下这类年金的现值不成问题。

［1］ BEEKMAN J A，FUELLING C P.Interest and mortality randomness in some annuities［J］.Insurance:Mathematics and Economics，1990（9）:185-196

［2］HE W J，ZHANG Y.Dual random model of increasing annuity［J］.Appl Math J Chinese Univ Ser B，2001，16（4）:430-438

［3］高建伟，邱菀华.随机利率下的生存年金模型［J］.系统工程理论与实践，2002（6）:97-100

［4］李长林，陈敏，顾勇.随机利率下的生存年金组合精算模型［J］.系统工程，2007（7）:116-118

［5］谢杰华，邹娓.随机利率下的连续型生存年金［J］.经济数学，2007（9）:229-233

［6］东明.随机利率下的联合寿险精算模型［J］.系统工程，2006（4）:68-72

［7］李秀芳.寿险精算实务［M］.北京:中国财政经济出版社，2006