矩阵最小奇异值下界的一种估计

张 丛，马丽宾，匡德胜

（重庆大学 a.数学与统计学院;b.通信工程学院;重庆 400044）

1 基础知识

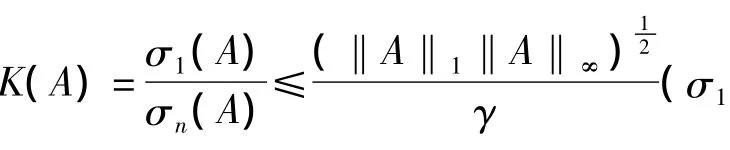
此处在黄廷祝利用分块矩阵求奇异值下界的估计的基础上进行了改进，得到了一个更精确的界值估计.

采用如下一系列符号:其中N表示自然数集;Mn（C）表示n×n阶复矩阵集合;λ（A）表示A的特征值;σn（A）表示A的最小奇异值;A*代表A的共轭转置;‖·‖表示向量范数诱导的矩阵范数.A奇异值用）表示.

将A的n个奇异值按降序排列，即σ1（A）≥σ2（A）≥…≥σn（A）.此外，设A=（aij）∈Mn（C），根据文献［3］将A分块为:

，则称A为对角占优矩阵，将具有这类性质的一切矩阵的集合记为A∈Ω.

2 主要结果

引理 2［3］设A∈Mn（C）分块如式（1），若A∈Ω，Aii（i∈K）为M阵，则 Reλ（A）＞0.

定理1 设A∈Mn（C）分块如式（1），若数α满足:

定理2 设A∈Mn（C）分块如式（1）.若数 α满足:存在x=（x1，x2，…，xk）T＞0，使得:

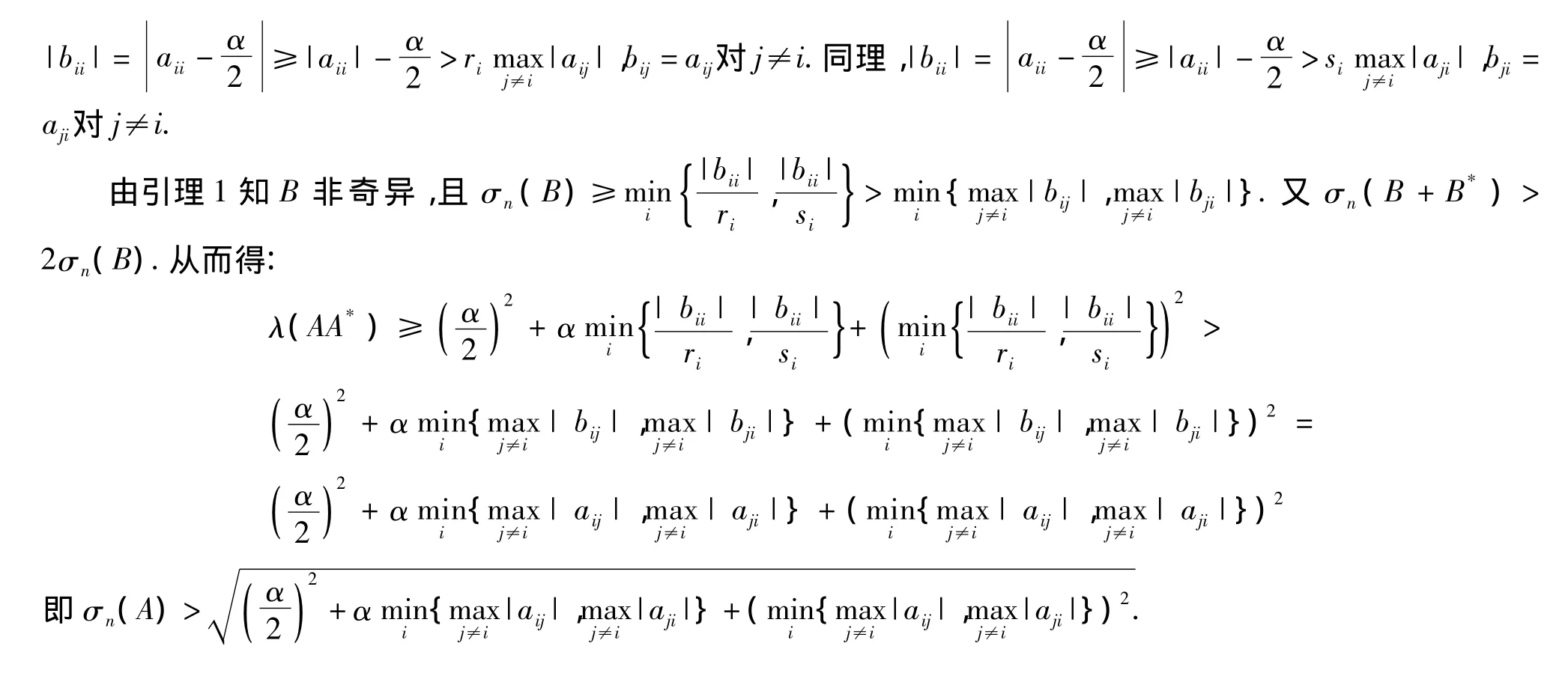
3 数值算例

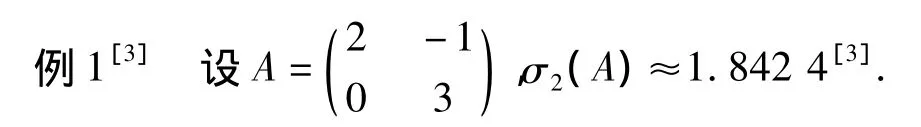
由文献［3］的结果为σ2（A）≥1.500 0.由此处可得σ2（A）＞1.500 0.

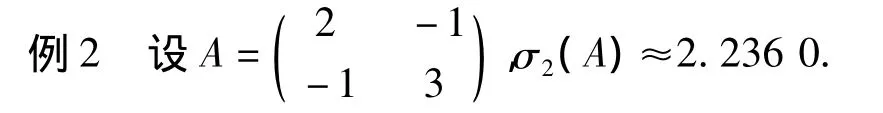
由文献［3］的结果为σ2（A）≥1.500 0.由此处可得，σ2（A）＞1.750 0.

显然此处的估计要比文献［3］中的估计更精确些.

［1］VARAH J M.A lower bound for the smallest singular value［J］.Linear Algebra，1975（2）:3-5

［2］JOHNSON C R.A Gersgorin-type lower bound for the smallest singular value［J］.Linear Algebra Appl，1989，112:1-7

［3］黄廷祝，游兆永.矩阵最小奇异值下界的估计［J］.计算数学，1997（4）:359-364

［4］LI H B，HUANG T ZH，LIU X P，et al.Singularity，Wielandt’s lemma and singular values［J］.J Comput Appl Math，2010，234:2943-2952