股指期货市场强行平仓风险估计

王永杰，陈 成，苏振华

（重庆大学数学与统计学院，重庆 400030）

随着我国金融体系的发展完善，股指期货市场等衍生品市场的建立已经开始进入日程，广大机构投资者和个体投资者面临着越来越多新的选择，同时也需要面对更多挑战，投资风险的度量就是众多挑战中最核心的问题之一。为了保证期货交易的顺利进行，有效控制违约风险，我国金融期货交易所实行交易保证金制度，保证金每日结算制度和强行平仓制度。从交易所的角度来看，这些制度是非常重要的，有利于控制市场违约风险，同时把交易所面对的担保风险降到最低。但是，从投资者的角度来看，结算制度是一把双刃剑，在减小投资者需要面对的信用风险的同时，给投资者带来了新的风险——强行平仓风险［1－5］。

长期以来，研究破产概率的问题都集中在保险精算领域，就所掌握的文献来看，很少看到讨论衍生品市场源于清算系统的投资风险的文献。此处们讨论的被迫平仓问题，是一个有限时间破产概率问题。即便是在保险精算领域，大部分的破产概率模型都是考虑的最终破产概率，也就是时间取得足够长条件下的破产概率，而讨论有限时间破产概率的文献并不多见。采用随机游走过程作为期货价格变化过程，采取随机过程的鞅方法对有限时间内无法追加保证金的概率给出了一个实用的计算方法，并将该方法应用于我国期货市场得到了投资者保证金总额和强行平仓概率之间的关系。

1 随机游走模型和平仓概率

大部分讨论保险公司破产概率的模型都是建立在复合Poisson过程的基础上，或者是复合Poinsson过程与其他过程（如Brown运动）的混合模型基础上。这些模型共有的特点就是认为随机到达的损失序列是一个独立同分布的随机变量序列，例如文献［6－11］，沿着这条思路，假定期货价格是一个独立增量过程，也就是说:

其中，Xi=Fi－Fi－1为交易缔结之日起的第i天价格增量，序列{X1，X2，…，Xn}是一个独立同分布的随机变量序列从而期货价格过程是一个从F0出发的随机游走过程。

假定每日价格增量来自状态空间χ={x1，x2，…，xk}，这个空间元素有限。对期货多头（long position）而言，如果期货价格上升，清算公司会将价格增量部分划入保证金账户，从而出现一个正的现金流;如果期货价格下降，清算公司会将价格下跌部分划出保证金账户，从而出现一个负的现金流。如果划出保证金后，客户账户上余额为负则需要追加保证金至规定水平。如果客户不能按时追加保证金，或追加保证金不足额，那么清算公司就会将该客户头寸进行部分或全部强行平仓，从而客户被迫减小持有量或离开市场。如果未来时间内期货价格朝有利方向变化，被平仓的头寸所带来的保证金损失也完全没有机会弥补，成为客户永久性损失。

对个人投资者而言，无法按时追缴保证金就意味着先期投入的保证金全部亏损，我们可以称为投资者破产。破产概率的大小和投资者持有的资金总量有很大关系。如果投资者手头资金充裕，那么源于强行平仓的造成的破产风险就会较小;如果投资者资金不充裕，又缺乏有效的融资渠道，比如市场上常见的散户，这些投资者破产的概率就较大。本研究的目的就是计算不同资本存量的期货投资行为的破产概率，从而为投资者，特别是散户投资者提供一种风险度量和控制的方法，以便更加有效的发现风险，管理风险和减小风险。

期货合约交易时需要缴纳交易保证金和维持保证金，我国金融期货交易所规定交易保证金为交易价格的10%，维持保证金按照每日期货价格涨跌盈余结算。我们假定投资者缴纳交易保证金后的账户余额为A，称为初始剩余资金。这笔资金用于每日结算是满足保证金追缴需要。我们假定投资者无法再次融资，一旦累积追缴保证金总额超过A，由于无法继续追加保证金，投资者被强行平仓。由于我们仅考虑拥有一份合约的投资，一旦强行平仓就意味着投资者破常，所以我们称这种情况为投资者破产，称累积追缴保证金总额超过初始剩余资金的概率为破产概率。我们这里讨论的期货投资是有限时间投资，假定期货寿命为N天。

定义随机时刻:Sn是从第一天到第n天追缴保证金账总额，T1是累计追缴保证金总额超过初始剩余资本的时刻，由于它的取值由X1，X2，…，Xn完全决定，所以T1是一个停时［12］，再定义停时:

也就是说，如果投资者在期货到期日前破产，那么τ=T1;如果投资者在期货到期以前都没有破产，那么τ=N。记累计到τ时刻追缴保证金总额为Sn，那么投资者破产概率pA为:

目的就是要计算pA的大小。

假定期货价格每日增量过程X1，X2，…，Xn是一个独立同分布随机变量序列，并且存在一个常数θ≠0，满足:

若设Zi=eθXi，就有E［Zi］=1。对累计保证金总额Sn，有:

由期货价格的每日增量过程的独立性，可知过程{Zi，i=1，2，…，n}也是一列独立同分布随机变量序列。从而随机过程{eθSi，i=1，2，…，n}是一个鞅。根据最优停止定理［12］，有:

引理 1 对任意的t∈{1，2，…，N－1，N}，有:

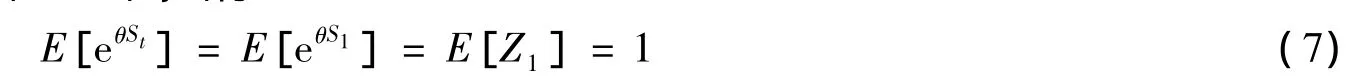
上述引理可以根据最优停止定理和鞅的定义得到，结合上述引理，有下面的破产概率计算公式。

定理1 设投资者在缴纳交易保证金后的剩余资本存量为A，每日期货价格变化过程为X1，X2，…，Xn，该过程为取值状态空间χ={x1，x2，…，xm}，m∈N的随机游走过程（randomwalk），也就是每日价格变化过程是一列独立同分布的随机变量序列。再假设存在常数θ≠0，满足E［Xi］=1，τ是破产时刻，那么破产概率为:

证明 由于τN，从而有E［τ］≤+∞，由鞅的最优停止定理，有:从而利用条件数学期望的性质，有:

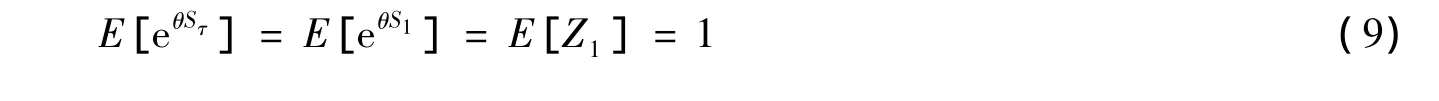
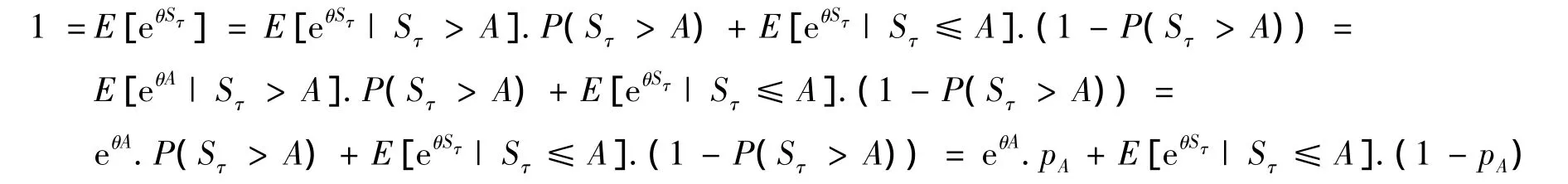
为了确定式（8），需要确定θ以及Lθ（A）。注意到θ必须满足式（5），可以用矩法估计来求θ的估计值.Lθ（A）是投资者在整个期货寿命时间以内都没有破产时，到期货到期日缴纳的交易保证金总额Sτ的矩目函数.也可以用历史数据估计这个值。

1.1 参数θ的估计

收集到期货价格每日增量数据为x1，x2，…，xn其中n是历史数据个数，数据按照时间顺序排列。由于θ满足关系（5），用样本矩替代总体矩，从而有:

从式（10）中解出参数θ，即得估计值θ^。

1.2 参数Lθ（A）的估计

收集到期货价格每日增量数据为x1，x2，…，xn，其中n数据个数，数据按照时间顺序排列。这里提出一种简便的估计方法。由于期货寿命是N天，如果连续N天的价格增量X1，X2，…，Xn满足

那么可以把这个SN作为一个累积缴纳保证金总额的观测值。我们选择游程长度为N的子序列估计SN。些子序列满足式（11），并且所有子序列都互不重叠，也就是用xi，1，xi，2，xi，N，i=1，2，…，m，其中m是数据中满足要求子序列的个数，计算Si，N=ΣNk=1xi，k从而SN的估计为:

2 Csi300指数期货的强行平仓概率

整理沪深300指数数据，分别计算了一份指数期货合约在寿命分别为20，30，40，55 d情形下的剩余资本存量和投资者破产概率，如图1。

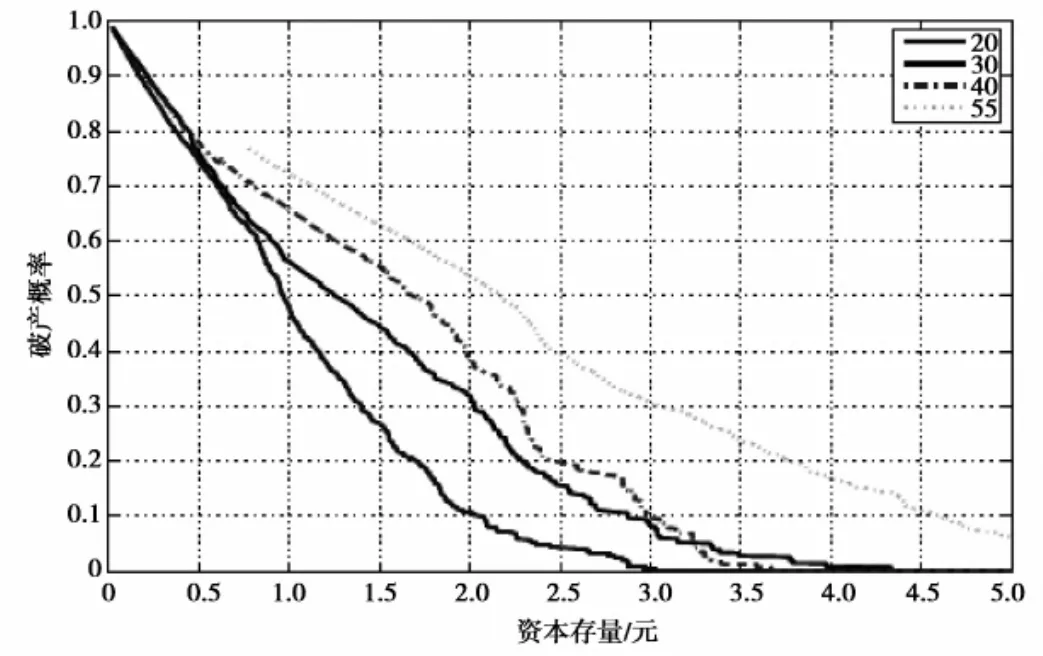
图1 Csi300指数期货市场破产概率和初始剩余资本的关系

从图1中看出:

（1）破产概率随着资本存量的增加而减少;

（2）一般而言，为了保证相同的破产概率，投资时间越长需要的资本存量越多;

（3）为了维持一份寿命在40 d以内的期货合约以90%以上的概率不被强行平仓，投资者需要至少30万块人民币以上的资本存量;为了维持一份寿命在55 d以内的期货合约以90%以上的概率不被强行平仓，投资者需要的资金在45～50万人民币之间。

从投资者角度来看，为了保证在有限的资金规模下投资的稳健性，减小每日结清带来的风险，必须严格控制投资规模。如果持有合约数量过多，现有资本存量难以满足维持头寸不被强行平仓的需要，那么投资者就需要积极的进行融资或者主动部分平仓，从而减小自己的风险暴露。

［1］赵彦辉，毅蒙，李粉娟.带干扰的变破产下限多险中风险模型［J］.重庆工学院学报:自然科学版，2010，24（3）:105-109

［2］马学思，刘次华.风险模型的破产概率［J］.数理统计与管理，2007，26（3）:440-443

［3］王泓娜.带干扰两险种风险模型的破产概率［J］.辽宁师范大学学报:自然科学版，2008，31（3）:275-277

［4］成世学.破产论研究综述［J］.数学进展，2002，31（5）:403-422

［5］PIRRONG S C.Metallgesellschaft:a prudent hedger ruined，or a wildcatter on NYMEX［J］.The journal of futuers markets，1997（5）:543-578

［6］张相虎，陈贵磊.带干扰的保费收取次数为poisson过程的破产概率［J］.山东科技大学学报，2005，24（1）:98-100

［7］龚日朝，李凤军.双poisson风险模型下的破产概率［J］.湘潭大学自然科学学报，2001，23:55-57

［8］BOROVKOV K A.DICKSON D C M.On the ruin time distribution for Sparre Andersen processwith exponential claim sizes［J］.Insurance:mathematics ＆ economics，2008，42:1104-1108

［9］PAULSEN J，KASOZI J，STEIGEN A.A numerical method to ˉnd the probbility of ultimate ruinin the classical risk model with stochastic return on investments［J］.Insurance:mathematics ＆economics，2005，36:399-420

［10］TANG Q H，TSITSIASHVILI G.Finite-and inˉnite-time ruin probabilities in the presence of sto-chastic returns on investments［J］.Advances in applied probabilty，2004，36:1278-1299

［11］DICKSON D C M，DREKIC S.The joint distribution of the surplus prior to ruin and the deˉcit atruin in some Sparre Andersen models［M］.Insurance:mathematics ＆ economics，2004，34:97-107

［12］ROSS S M.Stochastic Processes［M］.John Wiley ＆ Sons，INC，New York:1996