能量积分模型和拟合回归模型的应用

邓亚昊，游厚秀，陈金梅，李 爽

（重庆师范大学数学学院，重庆 401331）

1 问题分析

飞轮组由若干个飞轮组成，使用时根据需要选择几个飞轮固定到主轴上，这些飞轮的惯量之和再加上基础惯量称为机械惯量。一般假设试验台采用的电动机的驱动电流与其产生的扭矩成正比（比例系数取为1.5 A/N·m）;且试验台工作时主轴的瞬时转速与瞬时扭矩是可观测的离散量。工程实际中常用的计算机控制方法是:把整个制动时间离散化为许多小的时间段，然后根据前面时间段观测到的瞬时转速与瞬时扭矩，设计出本时段驱动电流的值，这个过程逐次进行，直至完成制动。问题一评价控制方法优劣的一个重要数量指标是能量误差的大小，建立电动机驱动电流依赖于可测量的数学模型。假设制动减速度为常数，初始速度为50 km/h，制动5.0 s后车速为零，计算驱动电流。问题二对于与所设计的路试等效的转动惯量为48 kg·m2，机械惯量为35 kg·m2，主轴初转速为514转/min，末转速为257转/min，时间步长为10 ms的情况。

2 模型的建立与求解

2.1 模型的假设

不考虑轮胎与地面之间的滑动;主轴的角速度与车轮的角速度一致;忽略车轮自身转动具有的能量;不考虑观测误差、随机误差和连续问题离散化所产生的误差;假设试验台采用的电动机的驱动电流与其产生的扭矩成正比;假设飞轮与转轴之间不存在摩擦力;不考虑转轴与飞轮之间产生的热量。

2.2 问题一模型的建立:能量积分模型

由于电动机驱动电流在试验台工作时主轴的瞬时转速与瞬时扭矩是可观测的离散量，根据前述要求，建立电动机驱动电流与可测量的数学模型。因此，从能量守恒思想出发可显而易见力矩做功等于刚体转动动能的增量，即应用刚体绕定轴转动的动能定理可建立能量积分模型，模型如下:

根据角加速度是角速度对时间的微分，所以可利用微分算得角加速度的公式如下:

式（1）中，ω表示转轴转动的角速度，由于一般假设试验台采用的电动机的驱动电流与电动机产生的扭矩成正比。因此列出驱动电流与扭矩的关系:

式（2）中，k=1.5 A/N·m在能量积分模型中，最主要的思想是能量的相互转化。根据能量转移思想可容易看出力矩做功等于刚体转动动能的增量，也就是刚体绕定轴转动的动能定理。考虑每一瞬时的能量变化，可得出能量的瞬时积分方程。设Mi为第i段时间的瞬时扭矩，ri为第i段时间的瞬时转速，J1和J2分别表示等效的转动惯量和机械惯量，ωi表示第i时刻的瞬时角速度。则可列出能量积分公式，如下:

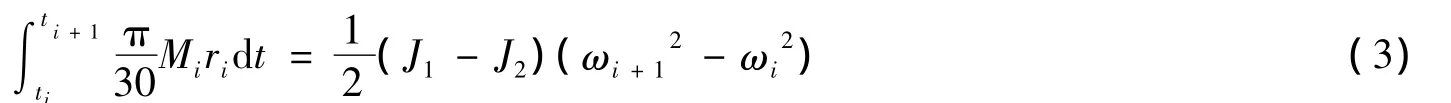
最后联立上述3个方程，即建立了完整的能量积分模型，得到驱动电流与瞬时转速与瞬时扭矩的关系。

2.3 问题一的求解

主要是利用上述模型——能量积分模型来求解。求解的思路是利用模型所建立的方程，将具体问题具体分析。列出能量积分方程，如下:

其中，R为前轮的滚动半径，ω1和ω2为转轴的初始角速度和末角速度，J1和J2为等效的转动惯量和机械惯量。根据角加速度的公式ω2=ω1+αt，可联立求得角加速度的值，将题目中已知数据代入式（2）求得电流产生的扭矩为116.38 N·m。根据驱动电流与其产生的扭矩之间的比例关系，计算出最终所要求得的驱动电流为174.57 A。

2.4 问题二模型的建立:拟合回归模型

对于问题二的模型建立，观测到时间、扭矩以及转速之间存在着一定的关系，又因为转速与角速度也存在一定关系。因此，可以运用Matlab拟合时间与角速度之间的关系，得到二者之间的函数关系。再由题意知，对于该方法的评价标准即为能量损失相对值的大小。若能量相对误差较小，则说明该种控制方法比较好。因此，只需求解出能量相对误差大小即可。通过上述思想:由物理知识可得能量损失为实际能量值与理论能量值之间的差值:ΔE=E实际－E理论，建立拟合回归模型。

（1）由Matlab拟合时间与角速度之间的拟合曲线，得到拟合曲线为图1。图1为最初的时间与角速度之间的拟合图，观察图1可知，其前段时间的观测数据与拟合数据误差较大。

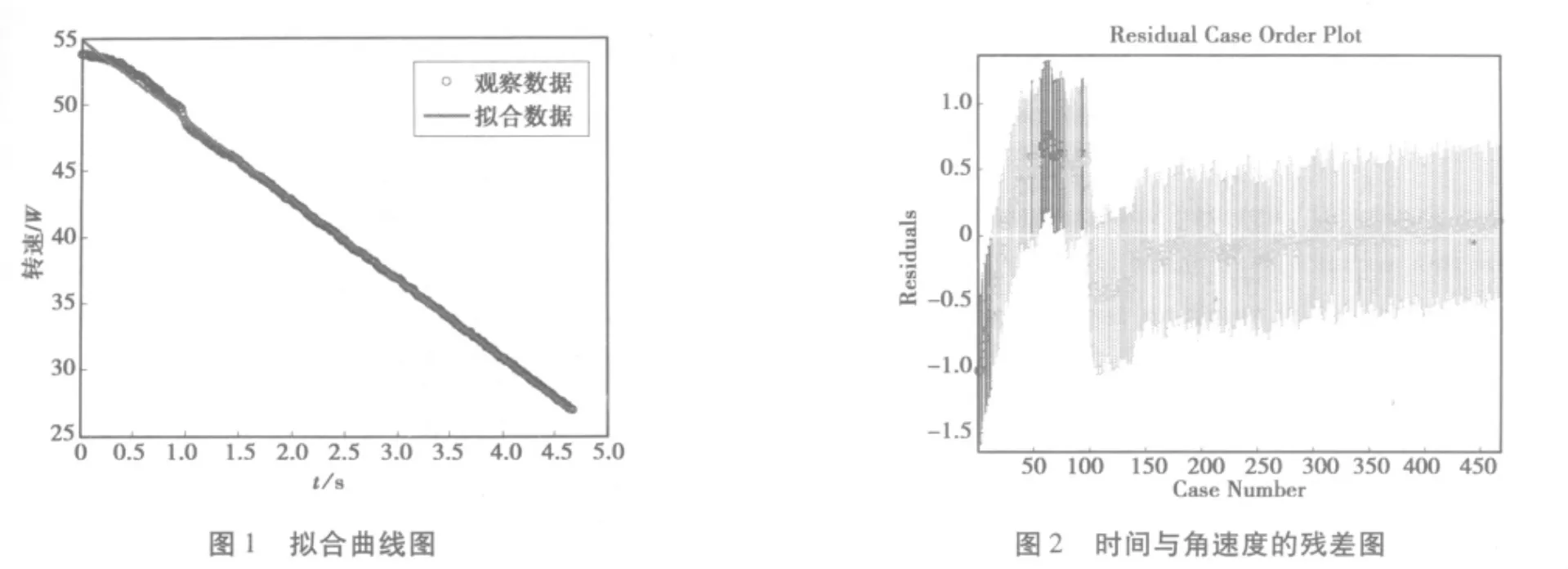
（2）作出时间与角速度之间的残差图，如图2所示。通过观察残差图可知，前100个数据偏离时间与角速度拟合的曲线较远，从而说明误差较大。因此对该拟合图进行了改进，则改进后的拟合图为图3。

观察图3便可发现该时间与角速度之间的拟合关系较好，因此采用图3的拟合图。发现时间与角速度成线性关系。通过数理统计知识可拟合出该直线。然后用Matlab编程求解出回归直线方程，回归方程为:

根据能量损失的公式求得能量的相对误差大小:

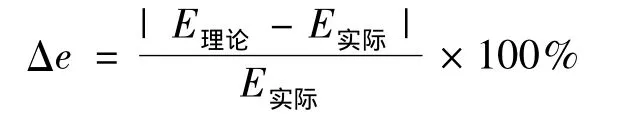
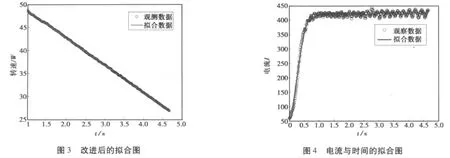
（4）评价标准。若相对误差较大，则说明该模型不符合。若相对误差较小，则说明该模型合理。从而判断该法的好坏。通过题目给出的扭矩与电流之间的关系，建立方程。将电流作为一种控制方法，由Matlab编程可同样拟合电流与时间之间的拟合图，拟合图形如图4，根据拟合图可发现拟合效果很好，因此采用该拟合图进行求解时间与电流之间的函数关系其方程如下:

I=t10－21t9+221t8－131 6t7+483 2t6－112 41t5+163 49t4－139 37t3+576 3t2－293t+64 （5）

由于分析题目后可发现控制方法的一个控制指标就是电流，因此式（5）也就是电流与时间构成的控制方程。

对于问题二的求解，利用上述拟和回归模型，可对题目给出的467个数据进行统计计算，计算出每一个能量的损失量，再进行分析。利用Excel统计计算出相对误差，如表1所示。

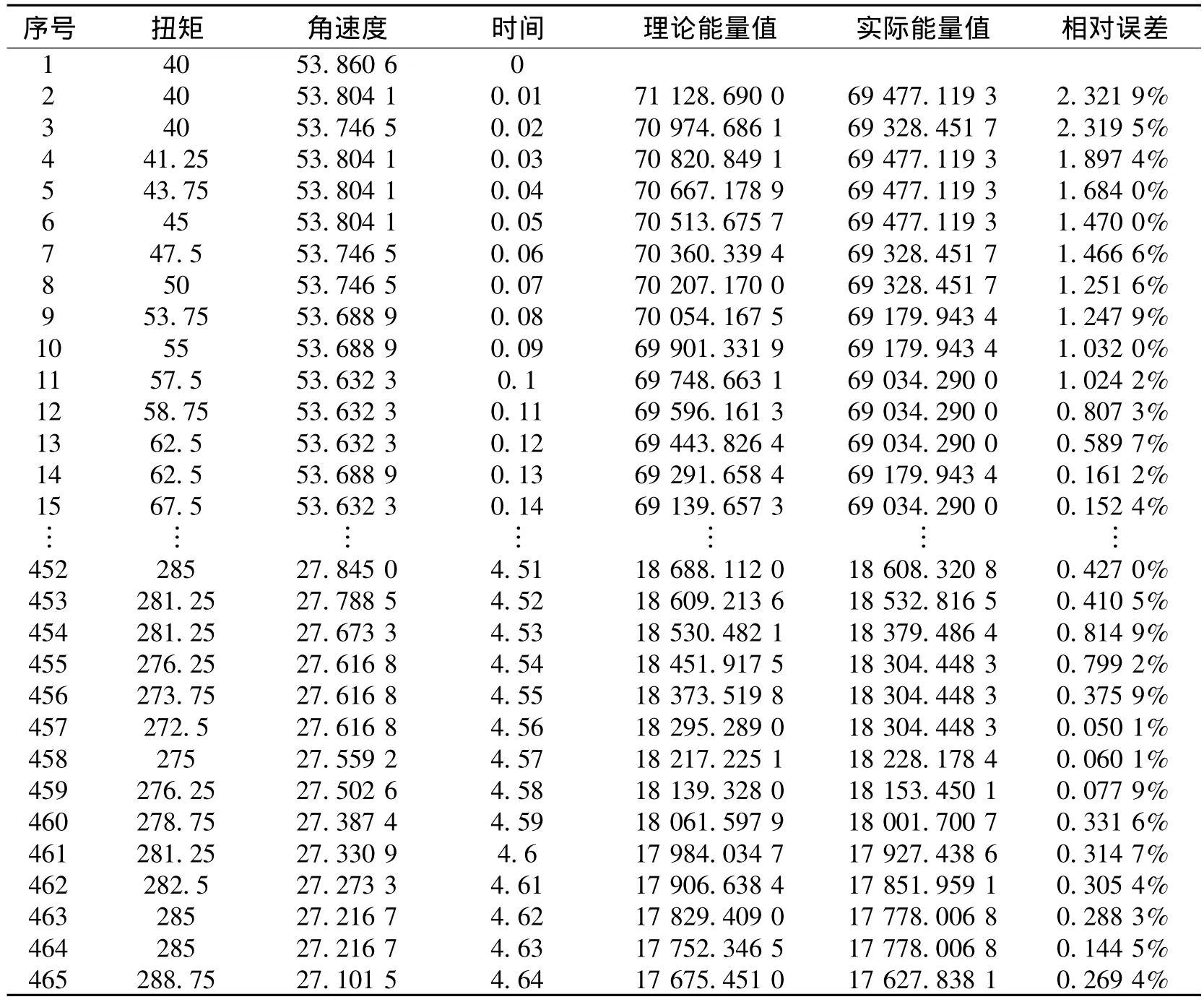
表1 相对误差表

根据表1可以明显看出能量的相对误差值最大也不超过2.5%，则说明该种控制方法具有可操作性。同时也说明该建模建立的较为合理，且数学逻辑性较强，精确度较高。

3 结果的评价及改进

汽车制动器的设计是车辆设计中最重的环节之一，直接影响着人身和车辆安全。为了检验设计的优劣，必须进行相应的测试。从材料及数据可知，问题的关键在于建立驱动电流与瞬时转速、瞬时扭矩之间的模型以及建立计算机的控制方法模型，解决这两个问题对整个方案起到了决定性的作用。总的来说，主要根据刚体绕定轴转动的动能定理，运用数学中的定积分知识，建立了能量积分模型，进而求解问题一。该模型具有较强的实用性，且考虑全面。模型二具有可操作性，与给出数据差距不大，相对误差最大不超过2.5%。

需要改进的方面:对于所建立的模型中转轴及飞轮均要产生温度，而温度产生的能量却在模型中没有考虑到。同时，模型二对该控制方法的结果评价有部分误差。

总的来说模型的建立具有特色性强及结合数学物理多方面知识具有综合性的特点，具有可操作性，结果合理。

［1］侯文华，梁冯珍.数学模型方法与算法［M］.北京:高等教育出版社，2005

［2］马文蔚.物理学［M］.北京:高等教育出版社，2006

［3］姜启源，谢金星.数学建模案例选集［M］.北京:高等教育出版社，2006

［4］赵静，但琦.数学建摸与数学实验［M］.北京:高等教育出版社，2000

［5］盛骤.概率论与数理统计［M］.3版.北京:高等教育出版社，2001