雷伞系统5自由度动力学模型

邓力涛, 曹小娟, 马 霞, 杨春武



雷伞系统5自由度动力学模型

邓力涛1,2, 曹小娟1, 马 霞1, 杨春武1

(1. 中国船舶重工集团公司第705研究所, 陕西 西安, 710075; 2. 水下信息与控制重点实验室, 陕西 西安, 710075)

空投鱼雷和火箭助飞鱼雷雷伞系统中, 降落伞的作用力简化为作用在雷尾且与气流方向一致的力, 而基于此建立起来的雷伞系统数学模型很难对雷伞系统的锥摆等做出准确的分析。为了解决这一问题, 该文从空气动力学的基本原理出发, 综合应用降落伞动力学、多体动力学的理论和分析方法, 利用牛顿和Kirchhoff方程建立了雷伞系统稳定下降阶段的5自由度动力学模型, 并进行了仿真分析, 仿真结果表明, 该系统具有较好的一致收敛和稳定性, 本文方法为开展降落伞工程设计提供理论参考。

空投鱼雷; 火箭助飞鱼雷; 降落伞动力学; 雷伞系统; 动力学模型; 5自由度动力学模型

0 引言

空投鱼雷和火箭助飞鱼雷作为立体反潜体系中最主要的组成部分, 在反潜中有着不可替代的作用, 受到各国海军高度重视。雷伞系统空中运动稳定性研究是空投鱼雷和火箭助飞鱼雷研制时的最主要研究内容之一。雷伞系统自由下降过程中, 如果其稳定性不好, 将出现空中摆动或围绕下降的轨迹作圆锥形摆动[1-2]。所谓锥摆是物伞系统摆动的一种形式, 是指伞的轴线与下降轨迹成一个倾斜角, 并围绕下降轨迹旋转的运动, 是系统不稳定的表现, 过大的摆动可能会影响运动轨迹, 特别严重时可能会使鱼雷中的组部件损坏。

研究结果表明, 以牛顿动力学为基础, 将降落伞的作用简化为作用在雷尾上且与气流方向一致的力而建立起来的雷伞系统数学模型很难对雷伞系统的锥摆等做出准确的分析。因此, 本文从空气动力学的基本原理出发, 开展基于降落伞多自由度运动的雷伞系统建模研究, 建立了适用于降落伞多自由度的雷伞系统空中弹道模型, 通过数值仿真, 验证了该运动模型具有较好的稳定性。

1 数学模型

1.1 基本假设

1) 降落伞是轴对称的, 伞衣完全张满时具有固定的形状。

2) 将雷伞系统看作是由2个刚体(伞衣和鱼雷)组成的系统, 在垂直平面内运动。连结点是一个铰链, 通过它只能传递力而不能传递任何力矩。因此, 在连结点沿降落伞Ox有一个内力F作用着。当把2个物体分开考虑时, 这个力就成为了一个外力。

3) 降落伞质量m和附加质量m的质心位于伞衣底边附近。有资料表明[1], 作用在降落伞上的空气动力的合力也作用在伞衣底边附近。为了简化运动方程, 将降落伞质心及其空气动力作用点两者都取在伞衣底边的中心O, 降落伞坐标系原点也取在O。

4) 载荷体为相对OX轴的轴对称物体。载荷体的重心不一定与它的气动力中心相重合。

5) 附加质量考虑其方向性。在Oy轴方向的附加质量写成m, 在Ox轴方向的附加质量写成m。

6) 降落伞绕Oz轴转动角速度和力矩M用和M表示; 载荷体角速度和力矩M用和表示。

1.2 坐标系

1) 地面坐标系

地面坐标系OXYZ固定于大地。坐标原点选取在雷体脱离运载体瞬间的雷体质心在地面上的投影位置;OY轴沿重力方向指向上;OX轴垂直于OY轴且指向运载体运动方向;OZ轴垂直于OXY平面, 且按照右手坐标法则与OX和OY构成直角坐标系。

2) 降落伞坐标系

降落伞坐标系OXYZ固连于降落伞系统。原点O选取在降落伞质心位置;OX轴为主轴, 与降落伞几何对称轴一致, 指向降落伞伞绳的拉力方向;OY轴垂直于OX轴, 当降落伞被水平拉直时,OY轴指向上方,OZ轴垂直于OXY平面, 与OX轴和OY轴构成右手系。

3) 雷体坐标系

雷体坐标系OXYZ固连于鱼雷系统。原点O选取在鱼雷系统质心位置;OX轴处于雷体对称面内, 与雷体几何对称轴一致, 指向雷头;OY轴处于鱼雷纵对称面内, 垂直于OX轴, 当鱼雷水平放置时,OY轴指向上方,OZ轴垂直于OXY平面, 与OX轴和OY轴构成右手系。

1.3 角度定义

1) 地面坐标系与降落伞坐标系之间的关系: 俯仰角——OX轴与水平面OXZ之间的夹角。当OX向上方倾斜时为正。

2) 地面坐标系与雷体坐标系之间的关系: 俯仰角——OX轴与水平面OXZ之间的夹角。当OX向上方倾斜时为正。

3) 攻角,:是雷体重心速度与雷体纵轴OX轴之间的夹角, 以在OX轴之下为正;是降落伞重心速度V与降落伞纵轴OX之间的夹角, 以V在OX轴之下为正。

坐标系及受力分析示意图见图1。

图1 5自由度雷伞系统

1.4 动力学方程

降落伞坐标系中, 降落伞动力学方程[3-5]

在雷体坐标系中, 雷体动力学方程

将转动角速度,看作是独立变量, 则

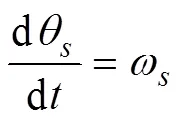
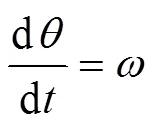
在上述7个方程中含有9个未知数:v,v,v,v,,,,,F。

由于2个刚体的转折点相对于地面坐标系的速度分量应该是相互相等的。从而得到2个附加方程, 即在大地坐标系上建立的附加方程。

OX轴

OY轴

式中:m­—— 载荷体的质量;

m­—— 降落的质量;

m­——轴上降落伞的附加质量;

m­——轴上降落伞的附加质量;

v和v­——伞衣质心速度在降落伞坐标系中ox和oy轴上分量;

v和v——雷体质心速度在物体坐标系中ox和oy轴上分量;

F,F,F,F——伞衣和雷体的气动力在降落伞坐标系中ox,oy和物体坐标系中ox,oy轴上分量;

,—— 降落伞和雷体的俯仰角;

——与ox轴的夹角;

,—— 伞衣质心和载荷体质心到转折点的距离;

——雷体绕通过载荷体质心oz轴的转动力矩;

——雷体绕通过雷体质心oz轴的转动惯量。

解得：

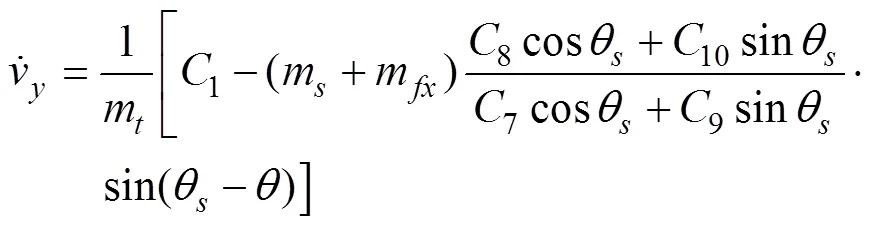
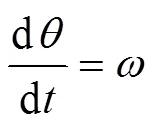
其中的参数为

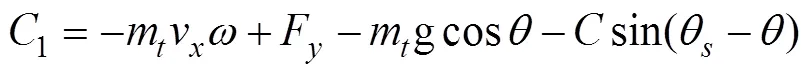
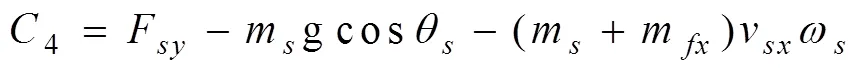
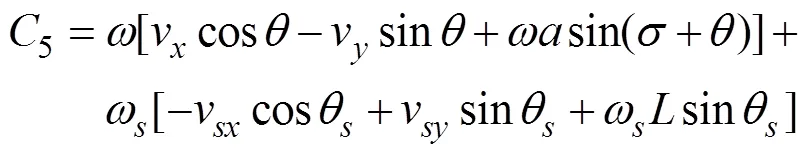
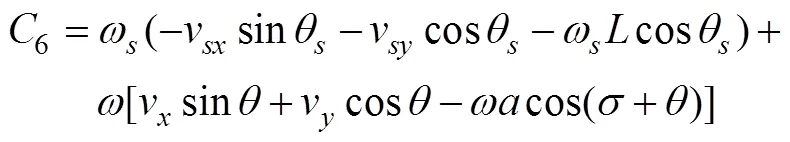
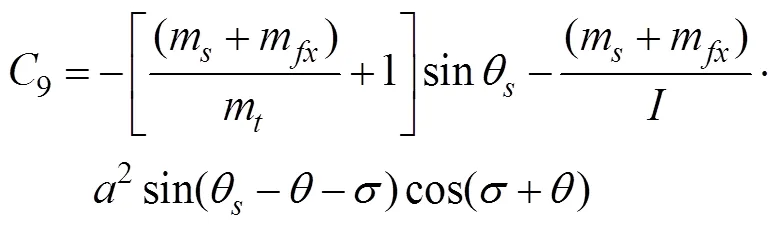
2 计算参数

1) 降落伞与雷体的气动阻力

方程中雷、伞气动力分量可用下式表示

同时由图可得气动攻角

式中:为大气密度;v为降落伞压心速度;C为降落伞法向气动力系数;C为降落伞切向气动力系数;0为伞衣名义阻力面积;为参考面积, 取雷体最大横截面积;为鱼雷质心的速度矢量;C为鱼雷的轴向力系数;C为鱼雷的法向力系数。

2) 降落伞的气动阻力系数

降落伞的气动力参数对物伞系统的运动模式有着重要的影响, Cockrell和Doherr就降落伞的气动力对物伞系统稳定性的影响做过一些研究, 本文在仿真中采用文献[6]~[8]中提供的气动力形式。

式中:为物伞系统攻角;0为物伞系统处于稳定滑行时的攻角;C和C分别为系统在稳定滑翔点处法向力系数变化率和轴向力系数变化率;C0为物伞系统在稳定滑翔下降时的轴向力系数。

根据式(16)和式(17)的气动力形式, 仿真中所采用降落伞的轴向力系数和法向力系数随攻角的变化曲线如图2和图3所示。

图2 法向力系数随攻角的变化曲线

图3 轴向力系数随攻角的变化曲线

3) 其他参数

降落伞质量m=0.75kg; 降落伞附加质量m=m=0.27 kg; 降落伞投影直径0=0.441 5 m2;转折点至雷体质心距离=0.278 m; 转折点至伞衣底边距离=1.82 m;

3 仿真分析

由图4和图5可以看出, 在所给初始条件下, 载荷体先以较大角速度剧烈的晃动, 但是在降落伞的气动阻力作用下, 经过一定时间后角速度和俯仰角均逐渐趋于稳定状态。表明在所给气动动力参数下, 该雷伞系统5自由度动力学模型具有较好的一致收敛和较好的稳定性。

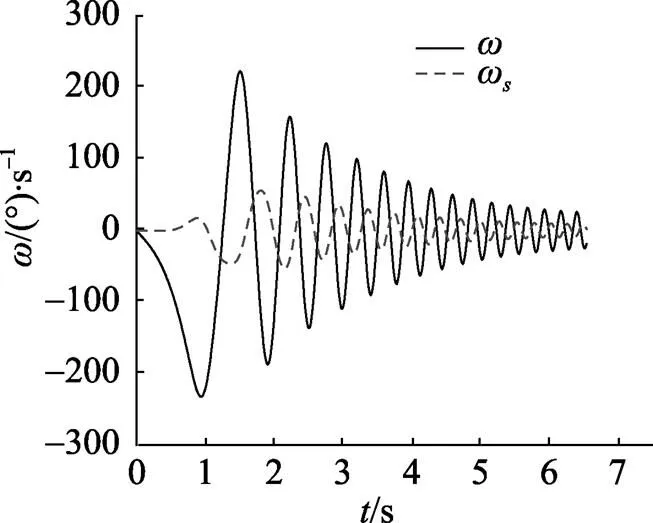
图4 雷伞系统角速度随时间的变化

图5 雷伞系统俯仰角随时间的变化

4 结束语

本文建立了雷伞系统5自由度动力学模型, 算例表明, 该运动模型所描述的运动渐进收敛, 具有较好的稳定性, 由于将雷伞系统动力学模型做了一定程度的简化, 因此本文是对雷伞系统空间运动模式的一个初步讨论, 进一步的研究需要建立更复杂的模型和试验数据的支持。

[1] Doherr K F. On the Influence of Stochastic and Acceleration Dependent Aerodynamic Forces on the Dynamic Stability of Parachutes[R]. AIAA-81-1941, 1981.

[2] Wolf D F, Heindel K. A Steady Rotation Motion for a Cluster of Parachutes [R]. AIAA 2005-1629, 2005.

[3] Etkin B. Dynamics of Flight - Stability and Control[M]. New York: John Wiley & Sons, 1996.

[4] 洪嘉振．计算多体系统动力学[M]．北京: 高等教育出版社, 1999．

[5] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997.

[6] 王海涛, 郭叔伟, 秦子增. 物伞系统空间运动模式分析[J]. 航天返回与遥感, 2009, 30(1): 21-26. Wang Hai-tao, Guo Shu-wei, Qin Zi-zeng, Modes in Space Motion of the Parachute-Payload System[J]. Spacecraft Recovery & Remote Sensing, 2009, 30(1): 21-26.

[7] 王海涛, 郭叔伟, 郭鹏, 等. 遗传算法在大型降落伞气动力参数辨识中的应用[J]. 宇航学报, 2010, 31(4): 981-985. Wang Hai-tao, Guo Shu-wei, Guo Peng, et al. Applicat- ion of Genetic Algorithms for Aerody- namic Parameter Estimation of Large Parachute[J]. Journal of Astronaut- ics, 2010, 31(4): 981-985.

[8] 汪清, 钱炜祺, 何开锋. 导弹气动参数辨识与优化输入设计[J]. 宇航学报, 2008, 29(3): 790-793. Wang Qing, Qian Wei-qi, He Kai-feng. Aerodynamic Parameter Identification and Optimal Input Design Formissile[J]. Journal of Astronautics, 2008, 29(3): 790-793.

Five-Degree-of-Freedom Dynamic Model for Torpedo-Parachute System

DENG Li-tao1,2, CAO Xiao-juan1, MA Xia1, YANG Chun-wu1

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710075, China)

In the conventional torpedo-parachute system, the effect of parachute is simplified to a force acting on torpedo tail and being along airflow direction, which leads to inaccuracy in numerical analysis of coning motion. According to the fundamental principles of aerodynamics, we establish a five-degree-of-freedom dynamic model of terminal descent of torpedo-parachute system based on the Newton and Kirchhoff formulas by applying the principles and analytical methods of parachute dynamics and multi-body dynamics. Simulation result demonstrates the reliable convergence and stability of the present system. This system may be applied to the engineering design of torpedo-parachute system.

aircraft torpedo; rocket assisted torpedo; parachute dynamics; torpedo-parachute system; dynamic model; five-degree-of-freedom dynamic model

TJ631.7; V445.23

A

1673-1948(2011)01-0001-05

2010-07-12;

2010-07-30.

邓力涛(1984-), 男, 在读硕士, 主要研究方向为雷伞空中弹道设计与控制.

(责任编辑: 陈 曦)