一种基于双圆域的AUV自主导航定位精度计数考核方法

张 宁, 张福斌,2, 鲍鸿杰, 张永清



一种基于双圆域的AUV自主导航定位精度计数考核方法

张 宁1, 张福斌1,2, 鲍鸿杰1, 张永清1

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 水下信息与控制重点实验室, 陕西 西安, 710072)

导航定位精度是自主水下航行器（AUV）一项重要的技术指标。基于概率圆计数考核方法, 取概率圆半径较小时, 当AUV的导航精度远低于指标时不利于快速做出判定; 而取较大时, 当AUV导航系统存在较大的系统偏差仍有可能判定为合格。针对上述不足, 该文根据AUV的基本轨迹及其航行轨迹测量的特点, 提出了一种基于双圆域的AUV导航定位精度计数考核方法, 通过研制方和用户方风险共担的原则合理调整2个圆域的半径, 不仅可以在AUV实际导航定位精度远低于指标要求情况下进行快速判定, 而且有助于降低导航系统的系统误差对考核的影响。仿真验证表明, 该方法科学、合理, 具有工程应用价值。

自主水下航行器; 导航定位精度; 考核; 双圆域; 概率圆

0 引言

自主导航定位精度是评价自主水下航行器(autonomous underwater vehicle, AUV)性能的重要指标, 特别是对于执行远程任务的AUV来说, 是其制定使用方法和进行任务规划的基本参数。AUV自主导航定位精度指标以圆概率偏差(circular error probability, CEP)的形式给出, 且CEP=%(为航程)。目前尚无相关的AUV自主导航定位精度考核标准。与导弹等实航试验属破坏性试验不同, AUV可重复使用, 故直接套用导弹等定位精度考核方法不合适。本文结合AUV的基本轨迹和轨迹测量特点, 借鉴导弹等命中精度考核方法[1-4], 提出基于双圆域的AUV导航定位精度的分析、鉴定及试验方法。

1 AUV基本航行轨迹

AUV的基本航行轨迹可分为管制、直航及导航3个阶段, 其水平面轨迹如图1所示。

图1 AUV水平面轨迹示意图

AUV由其载体发射后进入舵角管制阶段, 水平舵角和垂直舵角为管制舵角。管制阶段结束后, AUV进入直航阶段。在水平面内, 以发射时刻航向角为参考方位角, 进行航向控制, 并沿直线航行, 以期能安全离开载体。直航阶段结束后, AUV进入导航阶段。根据导航定位系统确定的当前所在经纬度与下一个航路点的经纬度, 进行制导律解算, 自主导航到下一个航路点, 导航过程如图2所示。

图2 AUV自主导航过程示意图

考虑到AUV在航行过程中, 受到海流及自身机动性限制等影响, 当AUV与航路点或航行终点的距离小于某一数值时, 即认为已到达该点。

湖上试验时, 测量AUV航行3D轨迹可采用工作在同步方式的长基线系统, 该系统由固定安装在水底的接收阵和安装在AUV上的同步声源以及数据处理中心构成。在海上试验中, 可采用船载短基线或超短基线系统, 基线系统工作在同步或应答方式下, 母船的位置通过差分全球定位系统(differential global positioning system, DGPS)获得, 受基线系统测量范围的限制, 母船只有在预定的航行终点附近才能获得AUV最后阶段的轨迹[5]。

2 基于双圆域计数考核方法及风险分析

在考核时, AUV可安排不同航程下的实航试验。由于研究的AUV导航定位精度指标是以CEP形式给出, 如果采用计量考核方法, 需要知道航程与航行终点散布误差之间的关系函数, 而在样本量较小的情况下, 这一关系函数要准确获得有困难, 故本文主要研究以AUV每条次试验导航定位精度判定为合格或不合格为基础的计数考核方法。

设AUV实际航行终点的纵向偏差和侧向偏差均服从正态分布(0,2), 则实际航行终点偏差在散布平面上概率密度函数为

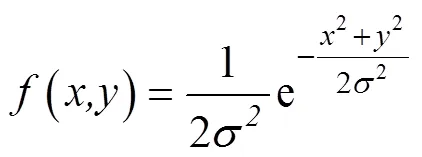
与=0.5对应的散布圆半径就是圆概率偏差CEP, 即

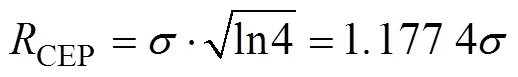
考核过程中, 实际航行终点的偏差如果不大于CEP, 则可判定为合格条次, 否则为不合格条次。假设考核的条次总数为, 那么当有=/2的条次数落到CEP圆内或圆外时, 即可判定产品的导航定位精度合格或不合格。另外, 为了降低用户方和研制方的风险, 考核的条次总数不宜取得过小。

以上均为采用基于单个圆域的概率圆对AUV的导航定位精度进行考核的方法, 当落入概率圆内的条次数取得较小时, 对于AUV导航定位精度远低于指标要求的情况不利于快速做出判断; 当取得较大时, 由于对应的概率圆半径较大, 此时如果导航定位系统的实际精度高于指标要求, 即使其存在较大的系统偏差, 仍有可能被判定为合格, 故用户方一般也不愿采用。

为了弥补以上考核方法的不足, 本文研究了一种基于双圆域的计数考核方法, 即根据指标CEP的值, 以预置的目标点为圆心, 分别取半径为1和2的2个圆域, 要求考核试验的条次总数中有1条次落入半径为1大圆, 且在这1条次中又有2条次落入半径为2小圆,1和2的具体数值根据双方风险共担的原则来确定, 并且小圆2的半径应与指标CEP的值接近, 以便较好地体现用户方对定位精度的要求。

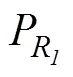
假设试验的条次总数取20, 以要求落入大圆内的条次数1取19、小圆内的条次数2取10为例, 按照研制方和用户方风险相当原则, 选取2组不同的圆半径时, 风险值如表1所示。

表1 2组双圆域对应的风险

由表1知,=1.3和圆半径分别为1.103 4CEP, 2.764 8CEP时, 双方风险相当, 均小于0.2, 是较为理想的考核方案。

由于要求落入大圆内的条次数1接近试验的条次总数, 故对于AUV实际导航定位精度远低于指标的情况, 可以很快给出不合格的结论, 便于研制方改进产品。

3 仿真分析

设AUV的导航定位精度指标为2%CED,取5 000 m, 则CEP=100 m, 换算成纵向和侧向标准差为84.93 m; 据此用MATLAB产生正态分布随机数的函数产生106个子样, 均值为0.001 5 m,标准差为84.92 m, 全部作为子样来考核是符合精度指标要求的。

从106个子样中随机抽取20个(纵向和横向)数, 相当于20条次的航行终点实际偏差, 利用这些样本评估AUV的导航定位精度。由于随机抽取具有一定的偶然性, 因此做了100组重复试验。依据大、小圆半径分别取2.764 8CEP，1.103 4CEP, 落入大圆内的条次数19、小圆内的条次数10时, 有78组合格, 与研制方的风险计算结果相符合。

若AUV实际导航定位精度为4%, 其他仿真条件保持不变, 仍作100组样本的重复试验均不合格。此时, 判定为不合格结束试验时的试验次数如图3所示。可见, 大多样本组可在少量条次试验后得出导航定位精度不满足要求的结论。

图3 仿真结果

另外, 以电罗经、多普勒速度仪和深度传感器构成的AUV导航系统为例, 当电罗经有0.8°的常值航向测量偏差时, 由此产生的常值侧向偏差约为1.4%。此时, 若AUV导航系统精度指标为2%, 不计系统偏差情况下实际导航定位精度为1%, 其他仿真条件保持不变, 仍作100组样本的重复试验, 依据大、小圆半径分别取2.764 8CEP，1.103 4CEP, 落入大圆内的条次数19、小圆内的条次数10时, 有13组合格; 而采用文献[5]提出的方法, 取为18, 对应的概率圆半径211.4 m时, 有95组合格。由此可以看出, 当导航定位系统存在较大的系统偏差时, 基于双圆域的计数考核方法同样可以取得较好的评定效果。

4 结束语

AUV的导航定位精度指标CEP值是一个概率值, 如何评定其是否满足要求, 是一个争议较大的问题。本文结合AUV的基本轨迹和航行轨迹测量方法, 研究了一种基于双圆域的计数考核方法, 在AUV实际导航定位精度远低于指标要求情况下, 该方法能够在少量的试验条次后得出结论, 并且较为充分地考虑了系统偏差对定位精度的影响。

[1] 程光显, 张士峰. 导弹落点精度的鉴定方法——概率圆方法[J]. 国防科技大学学报, 2001, 23(5): 13-17. Cheng Guang-xian, Zhang Shi-feng. Assessment for the Accuracy of the Fall Points ——Probability Circle Method[J]. Journal of National University of Defense Technology, 2001, 23(5): 13-17.

[2] 魏诗卉, 王明海. 导弹作战使用命中精度CEP评定方法研究[J]. 飞行力学, 2005, 23(4): 52-55. Wei Shi-hui, Wang Min-hai. Research on the Missile Operational Use CEP Assessment Method[J], Flight Dy- namics, 2005, 23(4): 52-55.

[3] 沙钰, 王正明, 程光显, 等. 弹道导弹精度分析概论[M]. 长沙: 国防科技大学出版社, 1995.

[4] 史志富, 张安. 空面导弹命中精度最优测试评定方法[J]. 飞行力学, 2004, 22(4): 34-37. Shi Zhi-fu, Zhang An. Hit Precision Evaluation of the M- issile with Optimal Test Method[J]. Flight Dynamics, 20 04, 22(4): 34-37.

[5] 高剑, 严卫生, 张福斌, 等. 概率圆方法在水下航行器制导精度鉴定中的应用[J]. 鱼雷技术, 2006, 14(1): 28-31. Gao Jan, Yan Wei-sheng, Zhang Fu-bin, et al, Asses- sment for the Accuracy of the Fall Points—Probability Circle Method[J]. Torpedo Technology, 2006, 14(1): 28-31.

A Count Assessment Method of Navigation Localization Accuracy Based on Dual Circular Area for AUV

ZHANG Ning1, ZHANG Fu-bin1,2, BAO Hong-jie1, ZHANG Yong-qing1

(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710072, China)

Navigation localization accuracy is an important technical index for an autonomous underwater vehicle (AUV). The probability circle assessment method is not easy to make a quick decision when the navigation accuracy is much lower than the accuracy index and the probability circle radius is selected too small, or it is possible to make a wrong decision when the navigation accuracy does not meet the index and the probability circle radius is set too big. To solve this problem, an assessment method using the dual circular area for underwater navigation accuracy is proposed in this paper. By properly adjusting radiuses of the two circular areas based on the principle of risk-sharing between the developer and the user, the proposed method can reduce the impacts of navigation system errors on assessment, and make quick decisions when AUV navigation accuracy is much lower than the navigation index. Simulation results demonstrate the feasibility and effectiveness of the proposed method.

autonomous underwater vehicle (AUV); navigation localization accuracy; assessment; dual circular area; probability circle

TJ630.33; TJ765

A

1673-1948(2011)01-0039-04

2009-11-28;

2010-05-04.

水下信息与控制重点实验室基金资助项目(9140C230503090C23)，船舶工业国防科技预研基金项目(08J4.2.2).

张 宁(1969-), 男, 在读博士, 主要从事水下航行器导航与控制技术研究.

(责任编辑: 杨力军)