基于MATLAB的太阳电池的I-U输出仿真

田汉民，计 伟，李毅杰

(河北工业大学信息工程学院，天津300401)

0 引言

太阳电池作为太阳能光伏发电系统的核心部分，已经成为研究太阳能光伏发电系统的重要环节。对太阳电池的输出特性进行仿真有助于获得太阳电池最大输出功率，以及达到最大输出功率时太阳电池的内部参数，从而提高能源的利用率。

MATLAB/Simulink仿真工具为复杂系统提供了简单、快捷、方便的建模仿真环境，可以实现建模与仿真、数据分析和曲线拟合、科学和工程绘图等功能，其中的电源系统工具库(Power System Bloekset)可直接为电力系统提供模块化仿真。

本文建立太阳电池I-U系统仿真的思路为:根据太阳电池的I-U输出的物理意义，推导典型太阳电池的光电流方程。根据光电流方程，通过程序仿真太阳电池的I-U输出。研究太阳电池的每个电学参数对电池效率、对I-U曲线形状及开路电压、短路电流、填充因子等性能指标的影响。以程序仿真结果为基础，对进一步提高性能做出预期。

研究太阳电池光电转换特性经常用到I-U曲线［1-3］，它可以直接提供电池的短路电流(Short-circuit current，Isc)、开路电压(Open － circuit voltage，Uoc)、填充因子(Fill factor，FF)和电池转换效率(The energy conversion efficiency，η)。自1839年法国物理学家A.E.Beequerel发现光生伏特效应以来，由固体物理知识推导出的太阳电池I-U方程和等效电路就成为研究太阳电池输出特性的基础［4，5］。

太阳电池的等效电路可以深层次地阐明太阳电池内部的物理化学机理，所以等效电路分析是进一步研究电池内部物理化学机理的一个重要手段，不但可以用于电池的系统模拟和电池批量性能类比，也可以深入理解电池内部电荷转移过程［6-11］。

1 太阳电池的等效电路和I-U方程的确立、仿真系统的建立

太阳电池的等效电路模型一般有3种:a.太阳电池的简单电路模型，不考虑任何电阻，该模型有利于理论研究，适于复杂的太阳能发电系统仿真;b.只考虑太阳电池并联电阻的模型，该模型精度稍高，在实际中不常应用;c.既考虑并联电阻，又考虑串联电阻的较精确仿真模型，其等效电路模型如图1所示［9］。

图1 太阳电池的等效电路

由太阳电池的等效电路模型，应用Kirchhoff电流定律，可得流过负载的电流I与其端口电压U之间的关系为:

根据图1太阳电池的等效电路，利用Matlab/Simulink仿真中的电源系统工具库(Power System Blockset)建立太阳电池的仿真模型，如图2所示。

图2 利用理想二极管建立太阳电池的仿真模型图

在实际测量太阳电池电流、电压时，不同时间测量的结果是有区别的，而且当考虑电容效应时，电容是一个时间敏感量，通过利用一个时钟源来控制测量时间。将控制受控电流源1的常数模块值设为0.0024，二极管的各项参数为:导通电压为0.7 V，体电阻为3 683 Ω，串联电阻值为38.1 Ω。点击运行按钮就可得到图3的仿真结果。

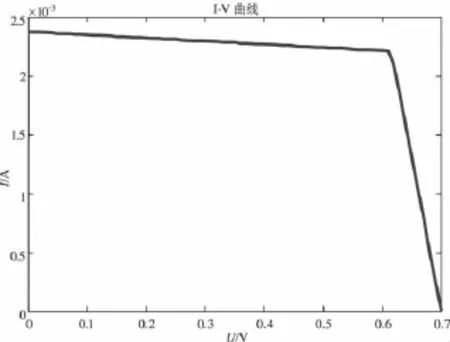
图3 利用MATLAB/Simulink仿真的太阳电池输出特性曲线

由仿真结果可得:太阳电池的输出特性曲线是由两条折线组成的。这是因为在该仿真模型中，二极管选用的是理想二极管，它只有两种状态，即导通和截止。当二极管处于导通状态时，流过二极管的电流趋于无穷大，当处于截止状态时，流过二极管的电流为零。当二极管导通时，整个电路的等效电阻就需要把二极管的内电阻考虑进去;相反，当二极管截止时则不需要考虑二极管内阻作用，这样就得到两条折线。加在太阳电池两端的电压大于0.7 V时，整个电路的电流都从二极管流过，因此在输出端测得的电流为零。

由前面的讨论可知:用理想二极管建立太阳电池的仿真模型所得到的太阳电池的输出特性曲线与太阳电池实际的输出特性曲线有一定的差距，这主要是因为在实际工作环境下二极管的伏安特性呈指数关系。因此，可以用一个函数模块来代替理想二极管建立仿真模型，这个函数模块就是实现二极管输出电流与输出电压的指数关系，如图4所示。

和利用理想二极管建立太阳电池仿真模型一样，将控制受控电流源1的常数模块值设为0.0024，内部并联电阻为 3 683 Ω，串联电阻值为 38.1 Ω。函数Fcn模块中用一个函数来表示，其表达式为:

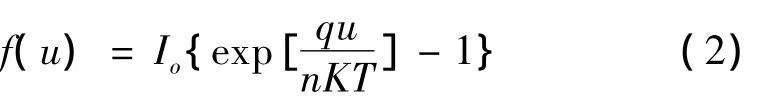
输入值u=U+IRs，因此经过此模块后可得流过二极管的电流Id，再经过受控电流源2流入到光生电流源处，在此要特别注意受控电流源2的参考方向，如图4所示。点击运行按钮就可得到太阳电池的输出特性曲线，如图5所示。

同理，改变仿真模型中各个模块值，可以得到不同的输出特性曲线，从而得出最大输出功率与各个参数的关系。

双击仿真模型图中的电阻Rs，在弹出的对话框中改变Rs值，每改变一次Rs的值点击一次运行按钮，然后在MATLAB命令窗口输入以下命令:plot(V，I)就可得到如图5所示的仿真结果。

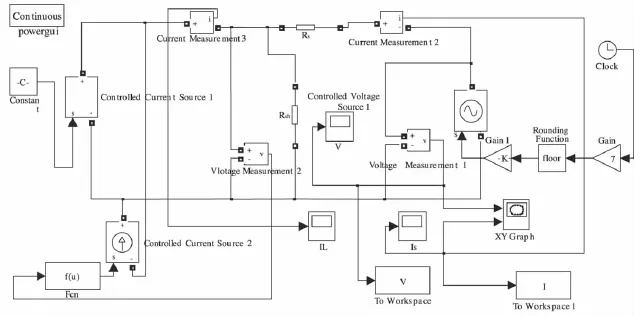
图4 利用函数模块建立的太阳电池仿真模型图

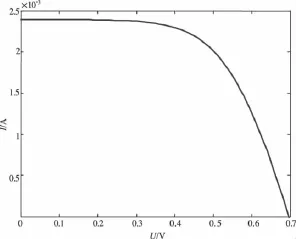
图5 太阳电池的输出特性曲线

由仿真结果图可知:Rs值越小，光伏电池输出特性曲线中平缓线段越长，弯度越大光伏电池的最大输出功率值越大;随着Rs的增大，平缓线段缩短，弯度减小，最大输出功率也随之减小。因此，在实际工程中Rs应尽量选取小电阻。这与用MATLAB命令得到的仿真结果图基本一致。

在仿真结果的基础上建立以下的界面图，如图6所示。

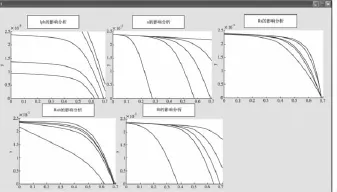
图6 界面图仿真结果

从图6可以得知:利用界面图仿真得到的结果与之前用M文件和用Simulink仿真所得到的结果完全一致。但它比前两种方法更具有优势，它使用户能够更加方便的得到太阳电池的输出特性仿真结果。

2 分析与讨论

2.1 主要性能参数

太阳电池的性能参数主要有开路电压、短路电流、串联电阻、并联电阻、填充因子、光电转换效率等。这些都在I-U仿真中有所体现:

(1)开路电压

开路电压Uoc是将太阳能电池置于100 mW/cm2的光源照射下，在两端开路时太阳能电池的输出电压值。

(2)短路电流

短路电流Isc是将太阳能电池置于标准光源的照射下，在输出端短路时流过太阳能电池两端的电流。

(3)串联电阻Rs

晶体硅太阳电池制作过程中由于扩散制结、印刷电极等操作，在电极与硅片的接触面上会产生接触电阻。上表面的接触电阻为栅线和总线与扩散层的接触面产生的电阻，下表面的接触电阻为背电极与基区的接触面产生的电阻。同时在太阳电池内部也存在基片电阻、扩散区的薄层电阻等。在运行时这些电阻和负载串联在同一回路上，称为电池的串联电阻。减小串联电阻可以提高太阳电池的短路电流。

(4)并联电阻Rsh

太阳能电池产生的电能中有一部分由于电池内部漏电流而损失。对于单晶硅和多晶硅电池，形成漏电的主要原因有:通过PN结的漏电流;沿电池边缘的表面漏电流:金属化处理之后沿着微观裂缝或晶界等形成的细小桥路而产生的漏电流。所有这些漏电流在理论上都可归结到电池并联电阻Rsh之中。

2.2 各参数的影响

仿真结果表明，光伏电池的输出特性呈非线性，并且每条曲线有且仅有一个最大功率输出点。输出功率受串联电阻Rs、内部并联电阻Rsh、光生电流源Iph、二极管反向饱和电流Io和PN结理想因子n的影响。在实际工程中，主要关心的是串联电阻Rs，内部并联电阻Rsh及光照强度对输出功率的影响。因为串联电阻越大线路损失就越大，光伏电池的输出功率就会降低，从而导致输出效率的降低;反之，光伏电池的输出功率将增加，输出效率会增大。由仿真结果也可以得到:Rs值越小，光伏电池输出特性曲线中平缓线段越长，弯度越大，光伏电池的最大输出功率值越大。对于Rsh来说，Rsh值越小，光伏电池输出特性曲线中平缓线段越短，弯度越小，光伏电池的最大输出功率值越小;随着Rsh的增大，平缓线段增长，弯度加大，最大输出功率也随之增加。由于光生电流Iph受日照强度影响比较大，而且与日照强度成正比例关系，所以光照强度对输出功率的影响是通过光生电流源起作用的，日照强度的大小直接影响太阳能光伏电池输出电能的多少。日照强度越强光伏电池的输出功率就越大，反之输出功率就越小。

从以上仿真可以得到:Rsh值越小，光伏电池输出特性曲线中平缓线段越短，弯度越小，光伏电池的最大输出功率值越小;随着Rsh的增大，平缓线段增长，弯度加大，最大输出功率也随之增加。但是，可以观察到当Rsh趋于无穷大与Rsh为100 Ω时的最大功率并没有增加太多，而Rsh值取得过大会增加电路中的功耗，因此，在实际工程中不宜无限制的增加Rsh的值。

随着Iph值的增大和Io值的减小，开路电压增大、短路电流也增大，光伏电池输出特性曲线弯度越大，光伏电池的最大输出功率值越大。Iph值和Io值越大，开路电压越大，光伏电池输出特性曲线弯度越大，光伏电池的最大输出功率值越大;随着Io和Iph的减小，开路电压减小、弯度减小，最大输出功率也随之减小。

n值越大，开路电压越大，光伏电池输出特性曲线中平缓线段越长，弯度越大，光伏电池的最大输出功率值越大;随着n的减小，开路电压减小，弯度减小，最大输出功率也随之减小。

Io值越小，开路电压越大，光伏电池输出特性曲线中平缓线段越长，弯度越大，光伏电池的最大输出功率值越大;随着Io的增大，开路电压减小，弯度减小，最大输出功率也随之减小。这与太阳电池的真实测量结果基本一致［10］。

3 结论

本课题针对MATLAB仿真环境，基于太阳电池的I-U函数关系式，直接利用Simulink软件包建立了太阳电池的仿真模型，通过调节短路电流和开路电压等太阳电池内部参数，方便且准确地模拟了太阳电池的工作情况。最后根据正确的仿真结果制作了一个图形用户界面。

［1］Zhang J J.Study on Zn(II)tetracarboxy phthalocyanine doped TiO2 electrode using electrochemical impedance spectrum［C］.Acta Physico－Chimica Sinica，2008，24(1):79-84.

［2］Murayama M，Mori T.Equivalent circuit analysis of dyesensitized solar cell by using one－diode model:Effect of carboxylic acid treatment of TiO2 electrode［C］.3rd International Conference on Molecular Electronics and Bioelectronics，2005，1:542-545.

［3］Fang X.Effect of the thickness of the Pt film coated on a counter electrode on the performance of a dye-sensitized solar cell［J］.Journal of Electroanalytical Chemistry，2004，570(2):257-263.

［4］赵富鑫，魏彦章.太阳电池及其应用［M］.北京:国防工业出版社，1985.

［5］Huang S Y.Charge recombination in dye-sensitized nanocrystalline TiO2solar cells［J］.Journal of Physical Chemistry B，1997，101(14):2576-2582.

［6］Virginia Y，Seng-Tiong H，Robert P H C.Modeling and simulation for dye-sensitized solar cells［J］.Applied Physics Letters，2008，92(14):143506-143510.

［7］Tornow J，Schwarzburg K.Transient electrical response of dye-sensitized ZnO nanorod solar cells［J］.Journal of Physical Chemistry C，2007，111(24):8692-8698.

［8］Hoshikawa T，Kikuchi R，Eguchi K.Impedance analysis for dye-sensitized solar cells with a reference electrode［J］.Journal of Electroanalytical Chemistry，2006，588(1):59-67.

［9］Han L Y .Improvement of efficiency of dye-sensitized solar cells by reduction of internal resistance［J］.Applied Physics Letters，2005，86(21):213501-213503.

［10］Liyuan H.Modeling of an equivalent circuit for dye-sensitized solar cells［J］.Applied Physics Letters，2004，84(13):2433-2435.

［10］Han L Y .Modeling of an equivalent circuit for dye-sensitized solar cells:improvement of efficiency of dye-sensitized solar cells by reducing internal resistance［C］.in 15th International Conference on Photochemical Conversion and Storage of Solar Energy.Paris，FRANCE:Elsevier France-Editions Scientifiques Medicales Elsevier.2004.