时间序列分解在短期电价分析与预测中的应用①

熊高峰，韩 鹏，聂坤凯

（湖南大学电气与信息工程学院，长沙 410082）

在电力市场中，准确的电价预测不仅有助于发电企业构造最优报价策略，实现自身利益最大化，而且有助于用户降低使用成本。因此，电价的分析和预测是电力系统中的一个重要研究领域。

到目前为止，电价预测的方法大致可以分为两类［1］：一类是基于实际物理仿真模型的预测方法；另一类是基于数学建模的预测方法。前者通过对电力系统和定价过程进行详细模拟来预测电价。该方法有助于对电价曲线进行详细了解，但是，它需要大量的系统参数和市场信息，因此，在大型电力系统中，该方法较难实施。后者主要通过分析影响电价的主要因素、建立合适的数学模型来对电价进行预测。相对于前者而言，该类方法具有建模简单和易于实施的特点，因此，成为电价预测研究的主要方法。目前已提出的数学模型主要有时间序列法（自回归模型和差分自回归滑动平均模型等）［2，3］和神经网络法［4～6］等。但是，由于电价不仅受到负荷需求和发电机组的影响，而且也受到网络结构、发电厂商报价策略及天气状况等的影响，因此，电价时间序列的演化过程十分复杂，存在很强的随机波动性。这使得采用传统的时间序列法或人工神经网络法来对电价进行预测时效果往往不是很理想，有必要进一步改进预测方法、提高预测精度。

本文从电价时间序列的特点出发，采用数学方法将电价时间序列分解成趋势分量、周期分量和随机分量三个组成部分，并且，分别建立合适的预测模型来进行预测，将所得的三个预测结果相加得到最终的电价预测值。对美国PJM电力市场中日前电价进行的仿真测试结果表明，该方法能明显提高预测精度。

1 电价时间序列的分解与分离

在本质上，电价时间序列是一个非平稳随机时间序列，它在不同时间范围内的均值和方差是不同的，具有异方差特性，其外在表现为波动性大、跳跃点多、价格尖峰明显、离散程度高［7］。由于难以准确预测出跳跃点和价格尖峰出现的时间和高度，因此，很难用数学方法直接对这种时间序列作准确预测。但是，从电价时间序列的演化过程来看，在一定时间内波动的电价具有一定的趋势性。并且，由于电价主要受到具有强烈周期性（又称季节性）的电力负荷的影响，因此，电价的波动中又表现出一定的周期性。从非平稳的电价时间序列中分离出趋势分量和周期分量后得到的随机分量是一个平稳随机时间序列［2，8］，相对于非平稳时间序列而言，其分析和预测变得相对容易。

一般而言，在电价时间序列中，工作日（周一至周五）电价与周末（周六至周日）电价相差幅度很大，呈现出不同的特点。因此，本文首先将电价时间序列分解成工作日电价和周末电价两个时间序列，然后，分别从中分离出趋势分量、周期性分量和随机分量三个组成部分。

1.1 基于移动平均法分离趋势分量

从时间序列中分离出变化缓慢的趋势分量的方法主要有移动平均法、指数平滑法和多项式拟合等方法［8］。本文采用移动平均法来分离电价时间序列中的趋势分量。

移动平均法MA（moving average method）是通过移动平均来消除时间序列中的不规则变动和其他变动，从而揭示出时间序列的趋势性，得出趋势分量。根据其利用历史数据的权重不同，可以分为简单移动平均法和加权移动平均法。本文采用简单移动平均法，其计算公式如下

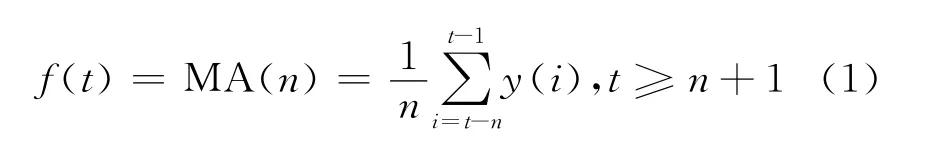
其中f（t）为移动平均值，即下一期的预测值；y（i）为i时刻时间序列的值；n为用于移动平均的时期个数。由移动平均法得到的各时刻的移动平均值所构成的序列即为趋势分量。

1.2 基于离散傅立叶变换分离周期分量

为了揭示电价时间序列中所隐含的周期信息和频域特征，本文采用离散傅里叶变换DFT（discrete fourier transform）及离散傅里叶逆变换IDFT（inverse discrete fourier transform）来从电价时间序列中分离出周期分量。

离散傅里叶变换［9，10］可以将离散时间序列变换为一组不同振幅、不同相位和不同频率的正弦信号的叠加。它是时间序列由时域分析转换到频域分析的重要工具，在工程中有着广泛的应用。

一个具有N个序列值的离散时间信号x（n）（n＝1，2，…，N），其离散傅里叶变换定义为［9，10］：

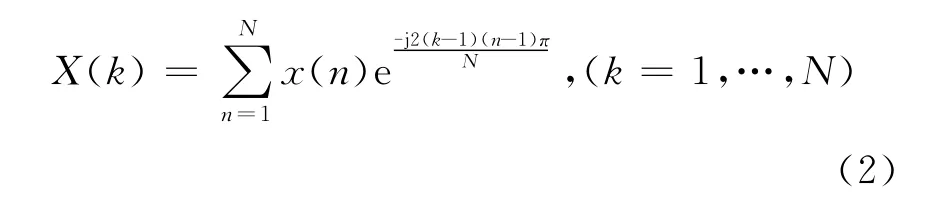
相应地，离散傅里叶逆变换定义为

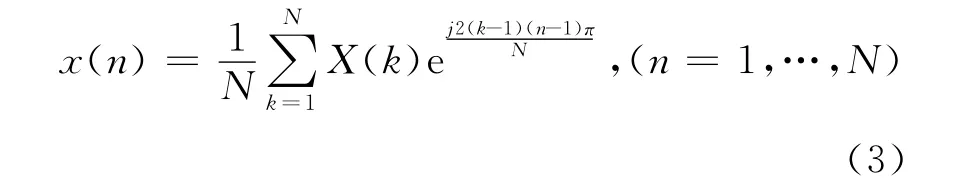
如果离散时间序列的采样周期为T，采样频率为f（＝1∕T），则对应的幅频图的横坐标轴上具有N个频率点，并且，前后频率点之间的频率间隔为Δf（＝f∕N）。频率轴上的第k个频率点所对应的时域周期信号的周期Tk为

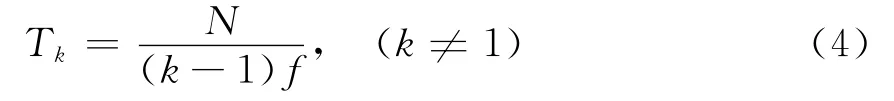
将分离出趋势分量后的电价时间序列进行离散傅里叶变换，得到对应的幅频图，从该图上提取幅值较大的频率点，然后进行离散傅里叶逆变换，就可以得到电价时间序列中所隐含的周期分量。

从电价时间序列中分离出趋势分量和周期分量后，就得到电价时间序列中的随机分量。通常，该随机分量是一个平稳时间序列，不含明显的趋势性与周期性。

2 电价预测

从上述电价时间序列的分解和分离过程可知，分离出来的趋势分量、周期分量和随机分量具有不同的变化特点，因此，需要采取不同的预测方法进行预测。在得到各个分量的预测值后，对其进行相加即可得到原电价时间序列的预测值。整个电价时间序列的预测过程如图1所示。

图1 电价预测流程Fig.1 Flow chart of electricity price forecasting

2.1 趋势分量的预测

趋势分量变化缓慢，波动性小，相对而言容易预测，预测方法也较为简单。由于本文采用简单移动平均法（见式（1））来从电价时间序列中分离趋势分量，因此，可将某一时刻的移动平均值作为其下一时刻的趋势分量的预测值，即下一期的预测值。

2.2 周期分量的预测

从电价时间序列中分离出来的周期分量是由一组不同频率、不同相位和不同振幅的正弦信号叠加而成，呈周期性变化。因此，在确定其变化周期后，由下式可以得到任意时刻t的周期分量的预测值。

式中：m为周期分量的变化周期；k为整数。

2.3 基于最小二乘支持向量机的随机分量的预测

由于随机分量波动较大，跳跃点较多，存在价格尖峰，因此，本文采用泛化能力较强、能够在较少学习样本下建模的最小二乘支持向量机LS－SVM（least square support vector machine）来进行随机分量的预测。

1）最小二乘支持向量机

支持向量机SVM（support vector machine）［11～13］是在统计学习理论的基础上发展起来的新一代机器学习方法。该算法的核心思想是通过非线性变换将输入向量映射到高维特征空间，然后在高维空间内利用结构风险最小化准则构造最优决策函数，并利用满足mercer条件的核函数来代替高维特征空间中的点积运算。最小二乘支持向量机是支持向量机的一种改进形式，它通过求解一组线性方程来取代支持向量机中凸二次规划问题的求解，减少了计算量并提高了收敛速度。

假设N个训练样本集合为｛（x1，y1），（x2，y2），…，（xN，yN）｝∈RD×R，D为R空间的维数，xi（i＝1，2，…，N）和y＝（y1，y2，…，yN）分别为输入向量和输出向量。用非线性映射Φ（x）将样本从原空间映射到高维特征空间H中，H为W维空间。在这个空间中构造如下最优线性回归函数

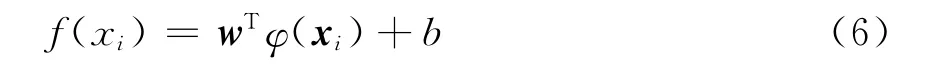
其中w为权向量，w∈RW；b∈R。根据结构风险最小化准则，该最优线性回归问题可以描述为以下约束优化问题。

目标函数

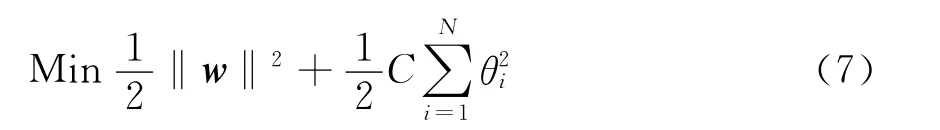
约束条件

其中θi为松弛变量，θi≥0；C为正则化参数，C＞0。

为了将上述约束化问题的求解转变成无约束优化问题的求解，建立Lagrange函数

其中a＝［a1，a2，…，aN］，ai为Lagrange乘子。最优的a和b取值可以通过库恩－塔克KKT（karushkuhn－tucker）最优条件得到，即取最优函数对w，b，θ，a偏导数为零，可得：

消去w和θ得到如下的线性方程组：

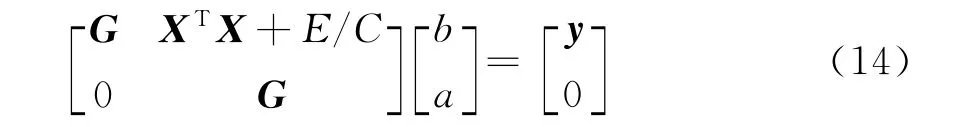
其中X＝［Φ（x1），Φ（x2），…，Φ（xN）］，G＝［1，1，…，1］，E为单位矩阵。

根据Mercer条件，定义核函数

利用上式可以将高维空间中的点积运算转化为求解低维空间中的核函数的值，这将大大减少计算量。在实际应用中，常采用径向基核函数：

这样，经过上述演化过程后，原最优线性回归问题可以通过最小二乘法求解，所求得的最优线性回归函数为

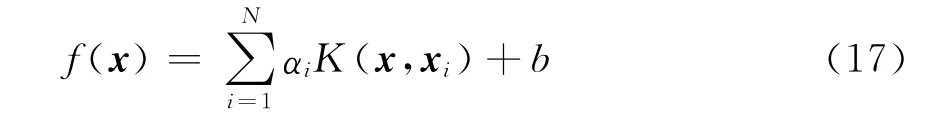
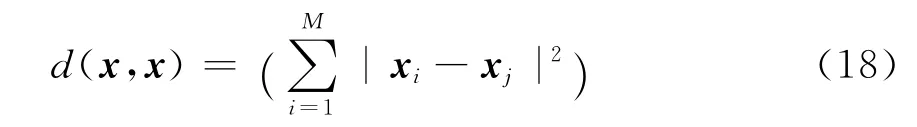
其中M为序列点的个数。

对随机分量的时间序列｛x1，x2，…，xM｝而言，计算任意t时刻序列值xt最邻近点xnbt＝｛xnb1，xnb2，…，xnb（M－1）｝，然后将这些最邻近点作为样本的输入，样本的输出则由这些最邻近点的下一时刻的序列值所组成。

2）参数的选取

由于参数C和δ2的取值直接决定最小二乘支持向量机的训练和泛化性能，因此，本文采用交叉验证算法［13］来寻求C和δ2的最优值。

3）选择训练样本的输入与输出

最邻近点法原理［14］表明相互之间最接近的对象具有相似的预测值，因此，本文使用最邻近点法选择训练样本的输入与输出。通过计算两点之间的欧几里德距离，选择距离最近的点作为最邻近点

3 实例验证

为了验证本文所提出的电价预测方法的有效性，在真实电价数据上进行了测试。并且，与采用传统三层BP人工神经网络的预测方法进行了比较。

1）测试数据

选取美国PJM电力市场western hub地区2007－04－23至2007－05－20的日前电价［15］作为训练和预测数据，其中2007－04－23至2007－05－13共计504个数据作为训练数据（图2），预测数据为2007－05－14至2007－05－20一周的日前电价。

2）比较对象

构建了24个传统的三层BP人工神经网络来预测每天24 h的电价。各神经网络的输入层、隐含层和输出层的神经元数目均分别为7、18和1。输出为预测日某时刻的日前电价，输入为该时刻前三小时的日前电价、以及预测日前三天和前一周同时刻的日前电价。各预测时刻的训练数据采用滚动方法进行训练与预测。

图2 电价时间序列Fig.2 Time series of electricity prices

3）性能评估指标

选取绝对百分比误差APE（absolute percentage error）和平均绝对百分比误差MAPE（mean absolute percentage error）作为电价预测方法的性能评估指标。

令Pactual为电价的真实值，Pf为电价的预测值，则

4）预测结果

首先，将原始电价时间序列分解成工作日电价和周末电价两个时间序列，然后，采用简单移动平均法（n＝24）分别从这两个时间序列中分离趋势分量。图3给出了工作日电价时间序列和其趋势分量。

其次，对分离出趋势分量后的电价时间序列进行离散傅里叶变换，得到对应的幅频图。图4给出工作日电价时间序列在分离出趋势分量后经过DFT得到的幅频图。图中，横坐标为频率点，纵坐标为幅值。

图5给出工作日电价时间序列中的周期分量。从电价时间序列中进一步分离出周期分量后，剩余的电价时间序列就为随机分量。图6给出工作日电价时间序列中的随机分量。

最后，采用本文提出的预测方法分别对工作日电价和周末电价两个时间序列中的三个分量进行预测。在采用LS－SVM对工作日电价中的随机分量进行预测时，C和δ2经过交叉验证法取值分别为64.30和12.87；而在预测周末电价中的随机分量时，其取值分别为5.95和1.67。

图3 工作日电价时间序列与趋势分量Fig.3 Weekday time series of electricity prices and trend component

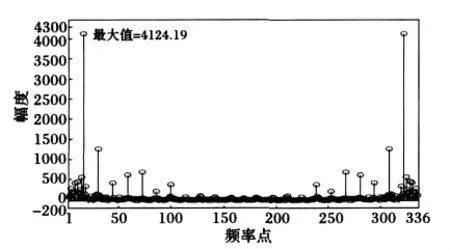
图4 幅度－频率点图Fig.4 Amplitude－frequency diagram

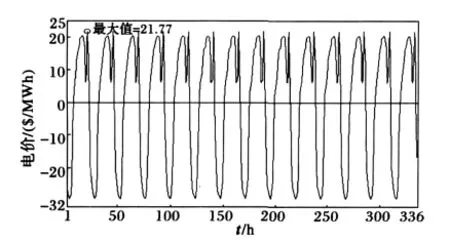
图5 周期分量Fig.5 Periodic component

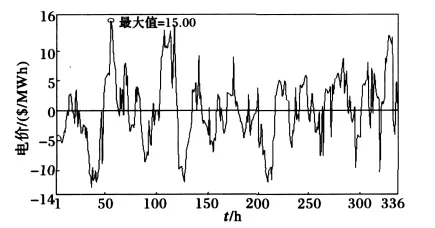
图6 随机分量Fig.6 Random component

图7给出分别采用本文提出的预测方法和采用传统三层BP人工神经网络预测方法来预测2007－05－14至2007－05－20一周的日前电价的预测结果。表1给出周五（2007－05－18）一天24 h的电价预测值和其真实值，以及两种预测方法的绝对百分比误差。表2比较了两种预测方法每天的平均绝对百分比误差。

图7 两种方法的电价预测结果和真实值Fig.7 Forecasted electricity prices by two methods and their actual prices

从图7、表1和表2的结果可知，相对于传统的三层BP人工神经网络预测方法而言，本文提出的电价预测方法在预测精度上有了较大改善，其平均绝对百分比误差在7%以内，而BP神经网络预测方法的平均绝对百分比误差在10%左右。同时，本文所提出的电价预测方法还减小了最大绝对百分比误差，增加了最大绝对百分比误差在10%以内的预测点的个数。因此，该方法是有效可行的。

表1 两种预测方法的预测误差比较Tab.1 Comparison of forecasting errors on Friday（2007－5－18）by two methods

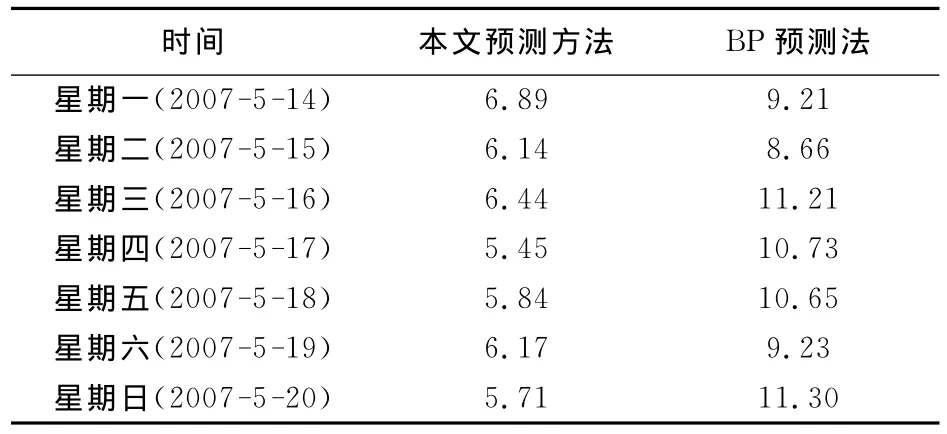
表2 两种预测方法的平均绝对百分比误差比较Tab.2 Comparison of the mean absolute percentage errors by two methods %

4 结论

本文在电价时间序列的分解和分离基础上，对从电价中分离出来的趋势分量、周期分量和随机分量采用不同的预测方法，来实现对原电价时间序列的预测。在随机分量的预测中，采用了泛化能力较强的最小二乘支持向量机方法。在真实电价数据上进行的仿真测试结果表明，本文提出的基于时间序列分解的电价分析和预测方法是有效的，能够显著提高电价预测的精度。

［1］ Lo K L，Wu Y K.Analysis of relationships between hourly electricity price and load in deregulated realtime power markets［J］.IEE Proceedings－Generation，Transmission and Distribution，2004，151（4）：441－452.

［2］ 周明，严正，倪以信，等（Zhou Ming，Yan Zheng，Ni Yixin，et al）.含误差预测校正的ARIMA电价预测新方法（A novel ARIMA approach on electricity price forecasting with the improvement of predicted error）［J］.中国电机工程学报（Proceedings of the CSEE），2004，24（12）：63－68.

［3］ Contreras J，Espinola R，Nogales F J，et al.ARIMA models to predict next－day electricity prices［J］.IEEE Trans on Power Systems，2003，18（3）：1014－1020.

［4］ Amjady N.Day－ahead price forecasting of electricity markets by a new fuzzy neural network［J］.IEEE Trans on Power Systems，2006，21（2）：887－896.

［5］ Li Zhang，Luh P B.Neural network－based market clearing price prediction and confidence interval estimation with an improved extended Kalman filter method［J］.IEEE Trans on Power Systems，2005，20（1）：59－66.

［6］ Fan S，Mao C，Chen L.Next－day electricity－price forecasting using a hybrid network［J］.IET Generation，Transmission ＆Distribution，2007，1（1）：176－182.

［7］ 张显，王锡凡（Zhang Xian，Wang Xifan）.短期电价预测综述（Review of the short－term electricity price forecasting）［J］.电力系统自动化（Automation of E－lectric Power Systems），2006，30（3）：92－101.

［8］ Peter J B，Richard A D.Introduction to Time Series and Forecasting［M］.New York：Springer－Verlag，2002.

［9］ 郑君里，应启行，杨为理.信号与系统［M］.北京：高等教育出版社，2000.

［10］康重庆，夏清，刘梅.电力系统负荷预测［M］.北京：中国电力出版社，2007.

［11］Vapnik V N.An overview of statistical learning theory［J］.IEEE Trans on Neural networks，1999，10（5）：988－999.

［12］肖先勇，葛嘉，何德胜（Xiao Xianyong，Ge Jia，He Desheng）.基于支持向量机的中长期电力负荷组合预测（Combination method of mid－long term load forecasting based on support vector machine）［J］.电力系统及其自动化学报（Proceeding of the CSU－EPSA），2008，20（1）：84－88.

［13］阎威武（Yan Weiwu）.支持向量机理论、方法和应用研究（Study of Support Vector Machines Theory，Algorithm and Application）［D］.上海：上海交通大学电子信息与电气工程学院（Shanghai：School of electronic，information and electrical engineering，Shanghai Jiao Tong University），2003.

［14］梁循.数据挖掘算法与应用［M］.北京：北京大学出版社，2006.

［15］PJM Market.Day－Ahead LMP Data［EB／OL］.http：／／www.pjm.com／markets－and－operations／energy／day－ahead／lmpda.aspx，2009－05－08.