神经网络与锁相环相结合的谐波检测方法①

（上海理工大学电气工程系，上海 200093）

随着电力电子技术的迅速发展，电网的谐波污染也日趋严重，由谐波引起的各种故障和事故不断发生，如今，谐波的危害已经引起了人们的高度重视。

有源电力滤波器是一种应用于动态抑制谐波的新型电力电子装置，它能对实时变化的谐波进行补偿，从而抵消电网中的谐波含量，使电能质量达到允许范围。在它的运行过程中，谐波的实时检测环节显得至关重要，如今，应用最为广泛的是基于瞬时无功功率理论的ip－iq谐波检测方法，但是，该方法中所用的低通滤波器使得该检测方法的实时性无法进一步提高，而且检测精度不高，是否有更好的检查方法，是人们所关注的问题［12］。人工神经网络的理论发展给谐波检测提供了新的研究途径，本论文提出一种基于BP神经网络与锁相环相结合的方法计算谐波分量，并通过MATLAB仿真验证了该方法的有效性，与ip－iq谐波检测方法的结果比较，该方法具有更好的精确性和实时性。

1 并联型有源电力滤波器的工作原理

并联型有源电力滤波器的工作原理如图1所示，图中，非线性负载产生谐波注入电网，有源电力滤波器通过CT分别检测出三相电网电流，经过谐波计算环节计算出除去基波以外的谐波分量，再将其调制成驱动信号以控制主电路（三相逆变桥）产生与电网谐波相位相反，幅值相等的谐波分量将电网谐波抵消，从而使电网电流波形逼近正弦波达到电能要求［3］。

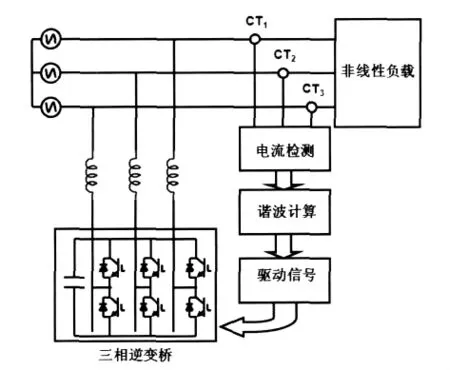
图1 APF结构原理图Fig.1 APF structure diagram

因有源电力滤波器工作在实时补偿谐波的状态，因此，它对谐波的检测环节有着很高的实时性要求。

2 基于i p－i q算法的谐波检测法

在APF的所有谐波检测方法中，基于瞬时无功功率理论的ip－iq谐波检测方法应用最为广泛，其原理如图2所示。

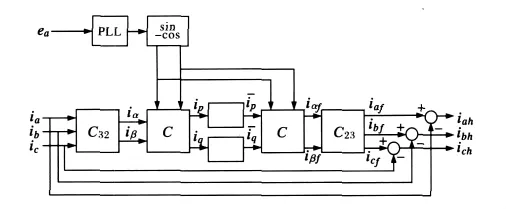
图2 ip－iq谐波检测方法的原理图Fig.2 Principle diagram of ip－iq harmonic detection

由三相电流ia、ib、ic经过与矩阵C32和C的运算得到ip与iq，具体运算过程如下：

其中

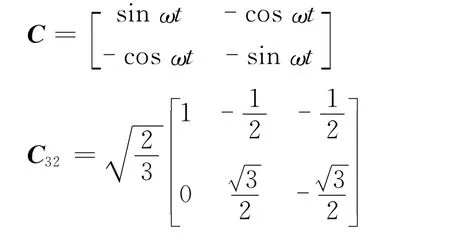
矩阵C中的正弦信号sinωt和余弦信号cosωt是由a相电压ea经过锁相环后得到的。

计算出的ip、iq经过低通滤波器得到它们的直流分量，这两个直流分量是由三相电流中的基波分量iaf、ibf、icf产生的，因此，再将这两个直流分量进行反变换便可得到三相电流的基波电流iaf、ibf、icf，具体运算过程如式（2）所示。

其中C23＝CT32

此时，只需要利用原来的电流信号与计算出的基波电流相减，就可以得到纯谐波电流［3］。

3 基于BP神经网络与锁相环相结合的谐波检测方法

作为使用最普遍的基于瞬时无功功率理论的ip－iq方法已经基本能满足APF的谐波检测，但因为有低通滤波器的存在，导致其在一定程度上不利于谐波检测的实时性，且检测精度也欠缺，在此提出了一种基于BP神经网络与锁相环相结合的谐波检测方法。

3.1 检测方法原理介绍

电力系统中，正常情况下的电流应为标准的正弦基波电流，其表达式如式3所示。

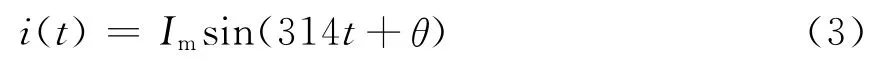
其中：Im为基波电流的幅值；θ为初相角。

从该式中可以看出，只要确定了基波电流的幅值Im以及初相角θ便可以得到基波电流的表达式，再与三相电流做差就可得到纯谐波电流。据此提出基于BP神经网络与锁相环相结合的谐波检测方法，其原理如图3所示，当电网侧三相电流经过锁相环时可得到与各相基波电流同相位，幅值为1的标准正弦信号iaf1（t）、ibf1（t）、icf1（t），再将其乘以由神经网络输出的三相电流基波幅值Iam（t）、Ibm（t）、Icm（t）便可得到当前时刻每一相电流的基波分量iaf（t）、ibf（t）、icf（t），此时，利用各相电流当前采样值ia（t）、ib（t）、ic（t）减去各自的基波分量iaf（t）、ibf（t）、icf（t）便可得到三相电流的实时纯谐波量iah（t）、ibh（t）、ich（t）。

该方法同ip－iq谐波检测方法一样，都是用当前检测的电流值减去计算出的基波电流值，因此，基波电流检测的精确性便决定了谐波检测的精确性。PLL锁相环不仅能将采样信号的干扰降到最低，而且能够根据三相电流产生出的参考信号产生非常完美的正弦波［19］，因此，该方法所检测出来的谐波具有精度高的优点，适合于APF的谐波检测。

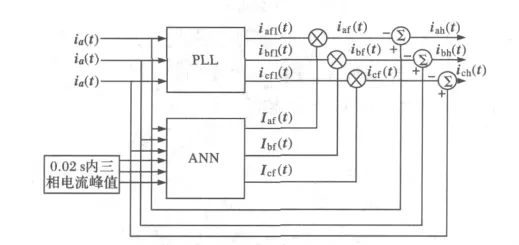
图3 BP神经网络与锁相环相结合的检测法Fig.3 Detection of BP neural network combined with PLL

3.2 用于检测基波幅值的BP神经网络

该检测方法中用于检测基波分量幅值的BP神经网络结构如图4所示。

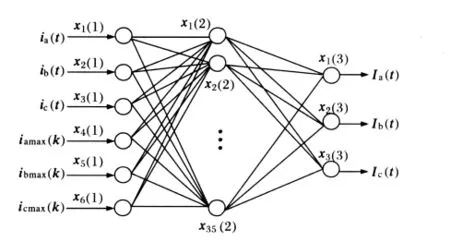
图4 用于幅值检测的BP神经网络结构Fig.4 BP neural network structure used for amplitude detection

该网络采用三层网络结构，第一层为输入层，共有6个神经元，其中ia（t）、ib（t）、ic（t）分别对应于三相电网电流的当前采样值，iamax（k）、ibmax（k）、icmax（k）是以一个工频周期（0.02s）为一周期，在该周期内分别计算出ABC三相采样电流的最大值；第二层为隐层，共有35个神经元；第三层为输出层，分别对应于三相电流的基波幅值Iam、Ibm、Icm，这三个量都可以通过快速傅里叶变换FFT（fast fourier transform）方法理论计算得出。隐层传递函数选择双曲函数f2＝2／（1＋e－2s）－1；输出层传递函数为线性函数f3＝s。

由于传统的BP算法在学习过程中有收敛速度慢、局部极值等缺点，在实际应用中，BP算法很难胜任，于是出现了许多的改进算法［17］。在此选择的是BFGS拟牛顿算法，该方法收敛速度快，能够很好地逼近目标精度而达到训练要求。而无论采用何种方法，其目的都是通过学习映射一个适合于该对象的网络权值及阈值。

将训练好的权值阈值带入网络得到隐层输出为

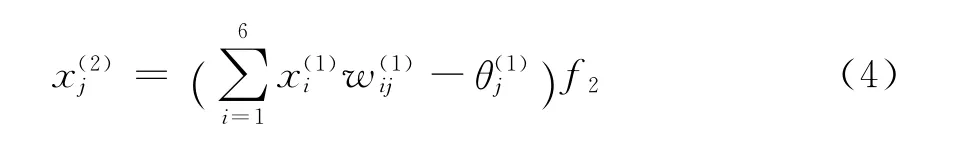
网络输出层为

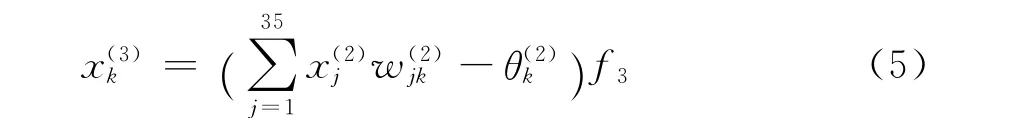
由式（4）、式（5）可以看出，本文所构造的前馈神经网络的输出与输入关系由加乘运算组成，避免了传统的ip－iq谐波检测方法中的低通滤波器成分因其传递函数所造成的延迟，所以在一定程度下提高了谐波检测的实时性。

4 仿真结果及总结

为了验证所述方法的有效性，本文建立了MATLAB仿真模型（图5，图6）。

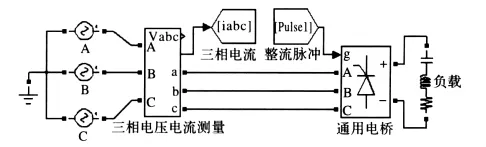
图5 谐波源的MATLAB模型Fig.5 Harmonic source model in MATLAB

仿真实验条件：三相电源带整流负载，其中，负载参数为R＝100Ω，L＝2 H，C＝1 F，在0.5 s时触发角由0°变为30°。

所有仿真结果以A相为代表，全过程中A相电流如图7所示，可以看到，在0.5 s时，触发角由0变为30°，电流波形发生了明显变化。

首先，取三相电流的采样当前值和以0.02 s为一周期分别计算前一周期内三相电流的最大值作为BP神经网络的输入，将FFT理论计算出的三相基波电流的幅值作为网络输出，按照之前阐述定义BP神经网络并进行离线训练，训练方法采用BFGS拟牛顿算法，由图8可见，在经过719次迭代后误差达到所要求的精度10－6。

将训练好的BP神经网络应用在该谐波检测方法中，将其检测结果与利用ip－iq算法检测的谐波电流波形对比。

两种方法检测的基波如图9、10所示，其中ip－iq谐波检测方法检测出的基波除了延迟大，而且输出波形的幅值也不稳定；相比之下，本文所提出的方法检测的基波延迟小，幅值稳定，且随着实验条件的改变而改变，具有良好的自适应能力。

两种方法检测出的谐波如图11、12、13所示，其中，图11显示了0～0.25 s内它们所检测出来的谐波电流，ip－iq检测方法要在0.2 s之后才能检测出谐波分量，而本文提出的方法在0.1 s之前就检测出了谐波分量。0.5 s时，整流装置的触发角发生变化，导致电流也随着发生变化，图12显示了本文方法在0.5－0.8 s内检测的谐波分量，0.55 s前就输出了稳定的谐波，而图13所示的ip－iq检测方法在0.7 s以后才能输出稳定的谐波。

图6 本文谐波检测方法的MATLAB模型Fig.6 Harmonic detection method of this paper in MATLAB

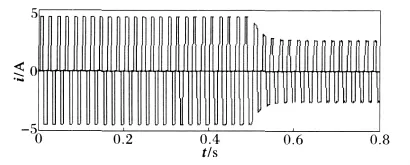
图7 A相负载电流波形Fig.7 Current waveform of A－phase load

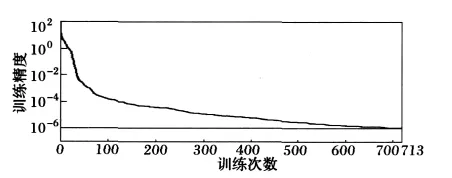
图8 BFGS拟牛顿算法的训练过程Fig.8 Training process of BFGS quasi－Newton algorithm

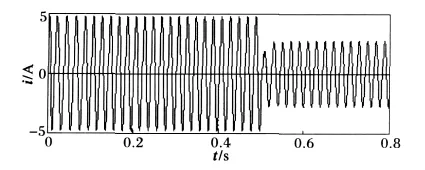
图9 本文方法检测的基波Fig.9 Fundamental wave detection in this paper

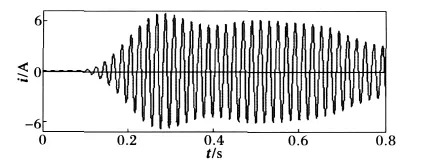
图10 i p－i q方法检测的基波Fig.10 Fundamental wave detection with i p－i q method

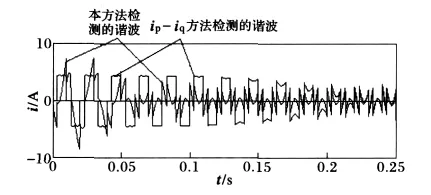
图11 0～0.25 s内两种方法检测的谐波Fig.11 Two methods of harmonic detection in 0～0.25 s

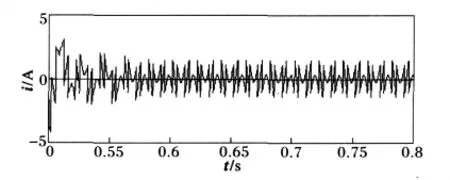
图12 0.5～0.8 s内本文方法检测的谐波Fig.12 Harmonic detection method of this paper in 0.5～0.8 s

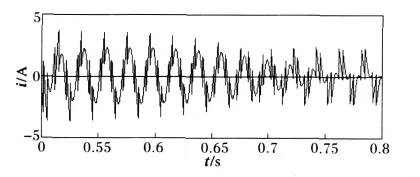
图13 0.5～0.8 s内i p－i q方法检测的谐波Fig.13 i p－i q method of harmonic detection in 0.5～0.8 s

5 结语

传统的ip－iq谐波检测方法实时性较差，检测精度也有很大的局限性。针对这些缺点，本文提出了一种基于BP神经网络和锁相环相结合的谐波检测方法，并且经过MATLAB的实验仿真验证了其可行性。通过与传统ip－iq谐波检测方法的比较，可以看出该方法具有良好的实时性和精确性以及自适应能力，满足APF的谐波检测要求，容易由DSP实现，且离线训练神经网络时，其目标输出容易计算。本论文中只改变了一次实验条件，在实际应用中，可搜集足够全的样本对神经网络进行训练，使其具有更强的鲁棒性和适应能力。

［1］ Pecharanin N，Mitsui H，Sone M.Harmonic detection by using neural network［C］∥IEEE International Conference on Neural Networks，Perth，Australia：1995.

［2］ 金明，刘远龙（Jin Ming，Liu Yuanlong）.用于电力系统谐波分析的ANN算法（A new ANN harmonic analysis algorithm for power system）［J］.电网技术（Power System Technology），1997，21（5）：52－54.

［3］ 王兆安，杨军，刘进军.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，1998.

［4］ Zin A A Mohd，Rukonuzzaman Md，Shaibon H，et al.Neural network approach of harmonics detection［C］∥International Conference on Energy Management and Power Delivery，Singapore，Singapore：1998.

［5］ 王群，吴宁，王兆安（Wang Qun，Wu Ning，Wang Zhao＇an）.一种基于人工神经网络的电力谐波测量方法（A measuring approach of power harmonics based on artificial neural network）［J］.电力系统自动化（Automation of Electric Power Systems），1998，22（11）：35－39.

［6］ Lixin Ma.The ability of higher order neural networks of consideration［J］.IEEE of Japan，1999，118（3）：421－422.

［7］ 胡铭，陈珩（Hu Ming，Chen Heng）.有源滤波技术及其应用（Active power filter technology and its application）［J］.电力系统自动化（Automation of Electric Power Systems），2000，24（3）：66－70.

［8］ Wang Qun，Wu Ning，Wang Zhaoan.A neuron adaptive detecting approach of harmonic current for APF and its realization of analog circuit［J］.IEEE Trans on Instrumentation and Measurement，2001，50（1）：77－84.

［9］ 李圣清，彭玉楼，周有庆（Li Shengqing，Peng Yulou，Zhou Youqing）.一种改进型自适应谐波电流检测方法的研究（Study on an improved adaptive harmonic current detecting method）［J］.高电压技术（High Voltage Engineering），2002，28（12）：3－4，13.

［10］肖雁鸿，毛筱，罗瑞琼，等（Xiao Yanhong，Mao Xiao，Luo Ruiqiong，et al）.神经网络理论在谐波测量中的应用（The application of neural network theory in the field of harmonic measurement）［J］.电工技术学报（Transactions of China Electrotechnical Society），2002，17（2）：101－104.

［11］孙驰，魏光辉，毕增军（Sun Chi，Wei Guanghui，Bi Zengjun）.基于同步坐标变换的三相不对称系统的无功与谐波电流的检测（Detection for reactive and harmonics currents of unbalanced three－phase system based on synchronous reference frame transformation）［J］.中国电机工程学报（Proceedings of the CSEE），2003，23（12）：43－48.

［12］张林利，王广柱（Zhang Linli，Wang Guangzhu）.一种基于人工神经网络的谐波测量新方法（New artificial neural network approach for measuring harmonics）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2004，16（2）：40－43.

［13］陈仲，徐德鸿（Chen Zhong，Xu Dehong）.一种基于DSP的高精度谐波检测改进方案设计（Improved design scheme of high accuracy harmonic detection based on DSP）［J］.电力电子技术（Power Electronics），2004，38（6）：53－55.

［14］崔景秀，王斌，王灏雄（Cui Jingxiu，Wang Bin，Wang Haoxiong）.基于dq坐标变换的谐波和无功电流检测法（A detecting approach of harmonic and reactive currents based on transformation of dq coordinates）［J］.通信电源技术（Telecom Power Technologies），2005，22（6）：47－50.

［15］汤胜清，程小华（Tang Shengqing，Cheng Xiaohua）.一种基于多层前向神经网络的谐波检测方法（A harmonic measuring approach based on multilayered feed forward neural network）［J］.中国电机工程学报（Proceedings of the CSEE），2006，26（18）：90－94.

［16］何英杰，邹云屏，李辉，等（He Yingjie，Zou Yunping，Li Hui，et al）.用于有源滤波器的一种新型谐波检测算法（Novel harmonic detecting algorithm applied to active power filters）［J］.电力电子技术（Power E－lectronics），2006，40（2）：56－58，65.

［17］葛哲学，孙之强.神经网络理论与MATLABR2007实现［M］.北京：电子工业出版社，2007.

［18］董长虹.MATLAB神经网络与应用［M］.北京：国防工业出版社，2007.

［19］周雪松，周永兵，马幼捷（Zhou Xuesong，Zhou Yongbing，Ma Youjie）.一种先进的APF补偿电流自适应检测法（An advanced adaptive detecting method of current compensation to active power filters）［J］.电力电子技术（Power Electronics），2008，42（4）：9－11.