不确定性电力系统鲁棒自适应励磁控制①

李啸骢，李文涛，徐俊华，张 鹏

（广西大学电气工程学院，南宁 530004）

随着电力系统大规模化、复杂化程度的增加，系统的动态品质对控制作用的要求也在逐步提高。电力系统是强非线性系统，许多非线性控制方法针对完全精确的模型取得了很好的控制效果［2，3］，同时电力系统又是不确定性系统，未知参数和各种干扰普遍存在，要设计出性能优良的控制器，必须充分考虑不确定因素的影响［1］。文献［4］针对电力系统外部干扰，利用线性H∞理论设计了反馈线性化的励磁控制。文献［5］考虑到系统参数不确定性，根据Lyapunov直接法设计了自适应励磁控制器。

耗散性是鲁棒控制理论中的重要思想［6］，利用γ耗散性与L2增益干扰抑制之间的联系，如能构造出保证系统γ耗散性的能量存储函数，便可得到闭环系统满足L2性能准则的反馈励磁控制器。

Backstepping设计在非线性系统控制中受到广泛关注［7，8］，其针对严格参数反馈的非线性系统，利用系统结构特性，将一个高阶系统分解成一系列低阶系统，递归地构造系统的Lyapunov函数，从而保证系统全局稳定。

本文通过Backstepping设计方法递归配置出系统的存储函数，得到的鲁棒自适应励磁控制器既对阻尼系数的不确定性具有实时估计的自适应能力，又对外部干扰具有抑制能力。存储函数同时又是Lyapunov函数，保证了闭环系统渐进稳定。最后通过单机无穷大系统的动态仿真验证了所设计控制器的正确性和有效性。

1 系统的数学模型

本文中发电机采用实用的三阶模型，单机无穷大电力系统SMIB（single－machine infinite bus system）结构如图1所示［1］。

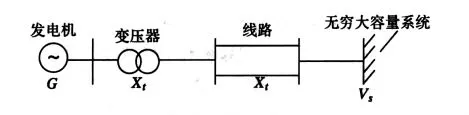
图1 单机无穷大电力系统结构示意图Fig.1 Structure diagram of single－machine infinite bus power system

具有励磁控制的数学模型［1］如下：

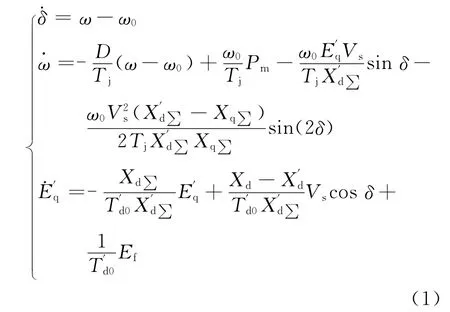
发电机端电压方程为

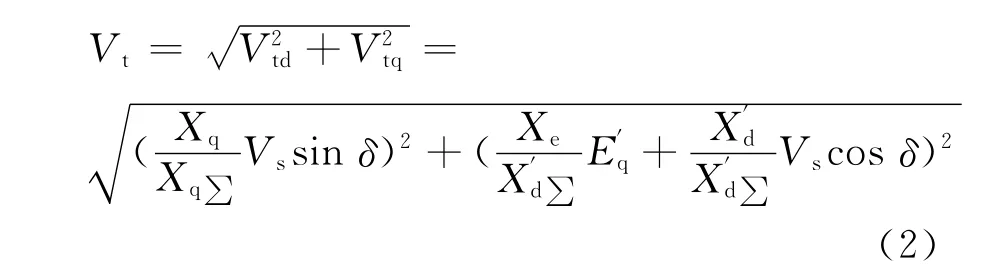
因为发电机阻尼系数D一般难以确定［5］，令

表示不确定参数；又考虑到系统中存在干扰

其中ε1和ε2是L2空间的未知函数，分别代表发电机转动轴上的扭矩干扰和励磁绕组的电磁干扰［9］。为了能够应用Backstepping设计，对系统方程取如下坐标变换：

其中δ0和ω0分别表示发电机功角和转速的稳态运行点。令已知常数

正当米多准备离去的时候，手臂却被一双钳子般的手抓住了。他大吃一惊，看起来手无缚鸡之力的老人哪来这么大的力气？

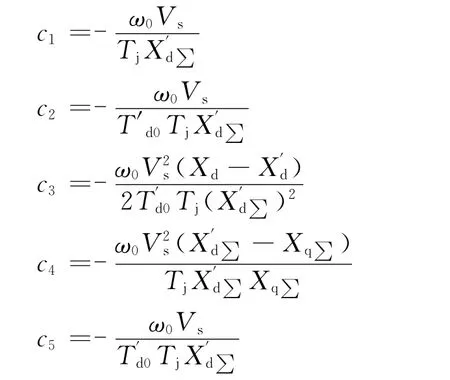
至此，考虑到不确定参数和干扰的系统模型化为

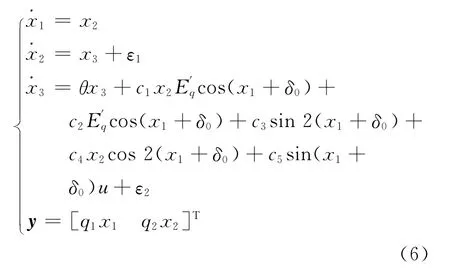
2 自适应鲁棒控制器设计

对于不确定性系统（6），求解非线性L2增益干扰抑制控制问题是指：构造系统的能量存储函数V（x），满足V（0）＝0，且对干扰输入ε满足如下耗散不等式

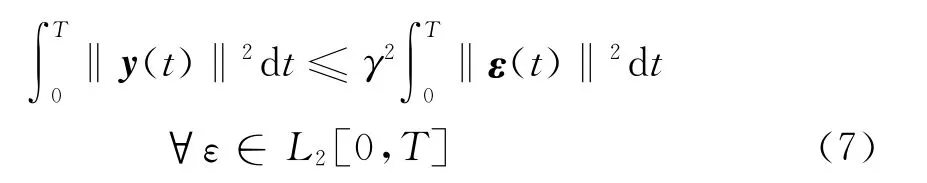
其中γ为给定正数。此时系统输出对干扰输入具有小于或等于γ的L2增益干扰抑制能力。

第一步 对于式（6）系统，首先考虑x1子系统，令x1＝z1。选取其Lyapunov函数其中σ＞0为可调参数。将x2看作子系统的虚拟控制输入，并令

其中z2为误差函数，α1是x2的虚拟控制，取α1＝－k1x1，其中k1＞0为可调整的控制器参数。对V1求导有

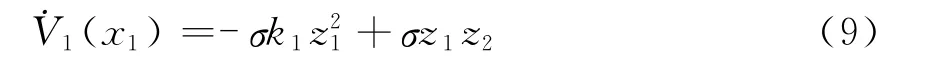
第二步 考虑系统（x1，x2），选取新的Lyapunov函数

为构造出耗散不等式（7），定义函数

注意到

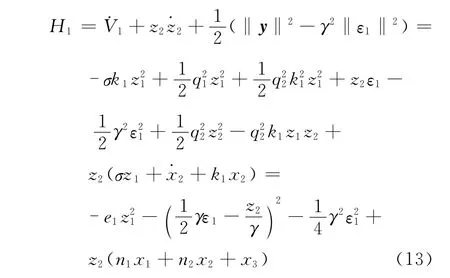
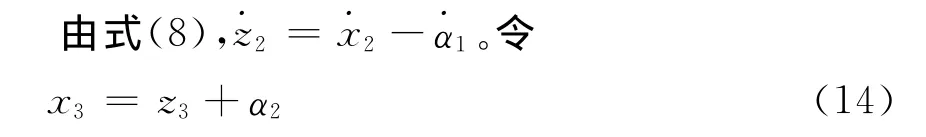
取x3的虚拟控制

其中可调控制器参数k2＞0，将式（14）和（15）代入式（13），则有

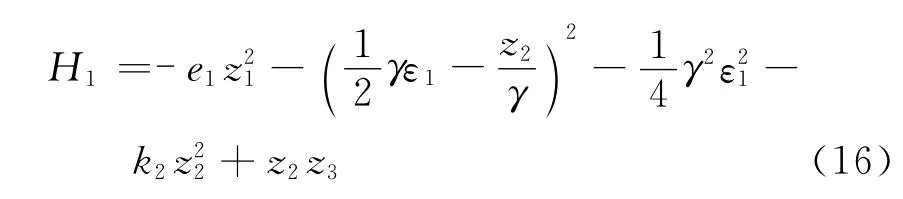
第三步 构造整个系统的Lyapunov函数，选取其中估计误差为θ的估计值，Γ＞0为自适应增益系数。定义函数

计算

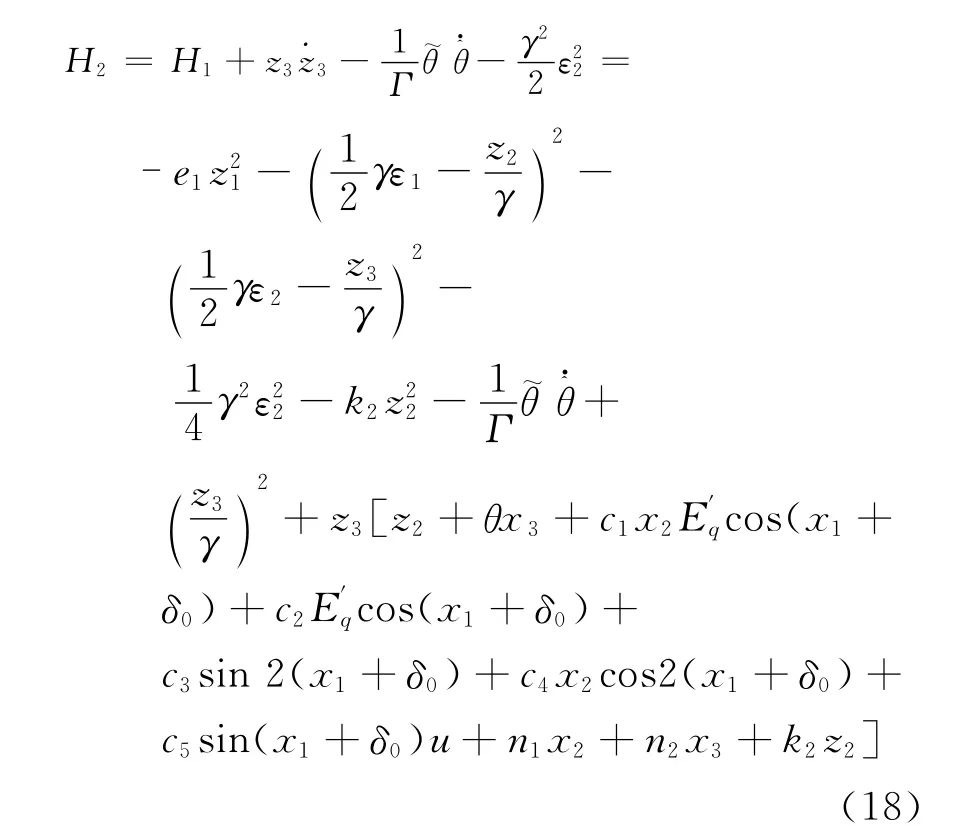
取控制律

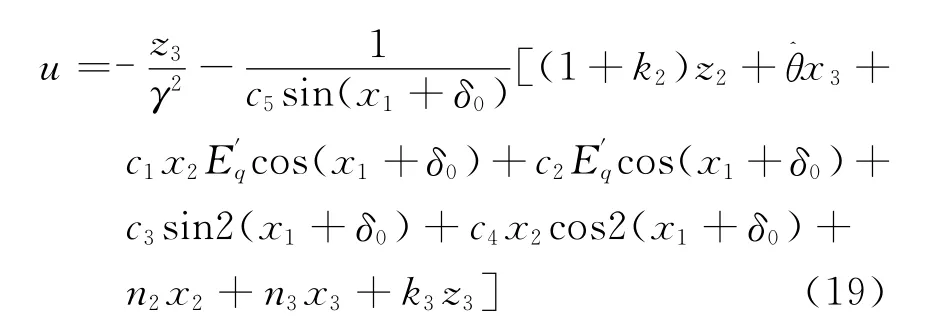
其中可调控制器参数k3＞0。参数自适应更新律

令系统的能量存储函数0），且V（0）＝0；˙V（x）＜0（x≠0），且˙V（0）＝0，故系统在平衡点Lyapunov渐进稳定；将式（22）代入（21）并对∀T＞0做积分即可得到不等式（7）。至此，便完成了对不确定性单机无穷大系统鲁棒自适应励磁控制设计。设计过程中未做任何线性化处

3 仿真研究

为验证控制器的鲁棒控制效果，对图1所示单机无穷大电力系统进行动态仿真，并与常规PID励磁控制器进行比较。模型参数为：Tj＝4.06 s；T′d0＝12 s；Xd＝2.5 p.u.；Xq＝2.5 p.u.；X′d＝0.25 p.u.；Xt＝0.1 p.u.；Xl＝0.3 p.u.。系统稳态工况为δ0＝30°；Vt0＝1.1325 p.u.。选择加权系数q1＝0.4，q2＝0.6，干扰抑制常数γ＝0.6。因阻尼系数D难以精确测量，设其实际值在1～5 p.u.内，在PID控制器中取为3 p.u.。令干扰ε1＝ε2＝1 p.u.。

仿真以下两种情况：

（1）系统由初始状态进入稳态后，在0.5 s时出现干扰ε1，在1.5 s时出现干扰ε2，干扰在出现后一直存在。系统有关状态量的动态响应曲线由图2给出。

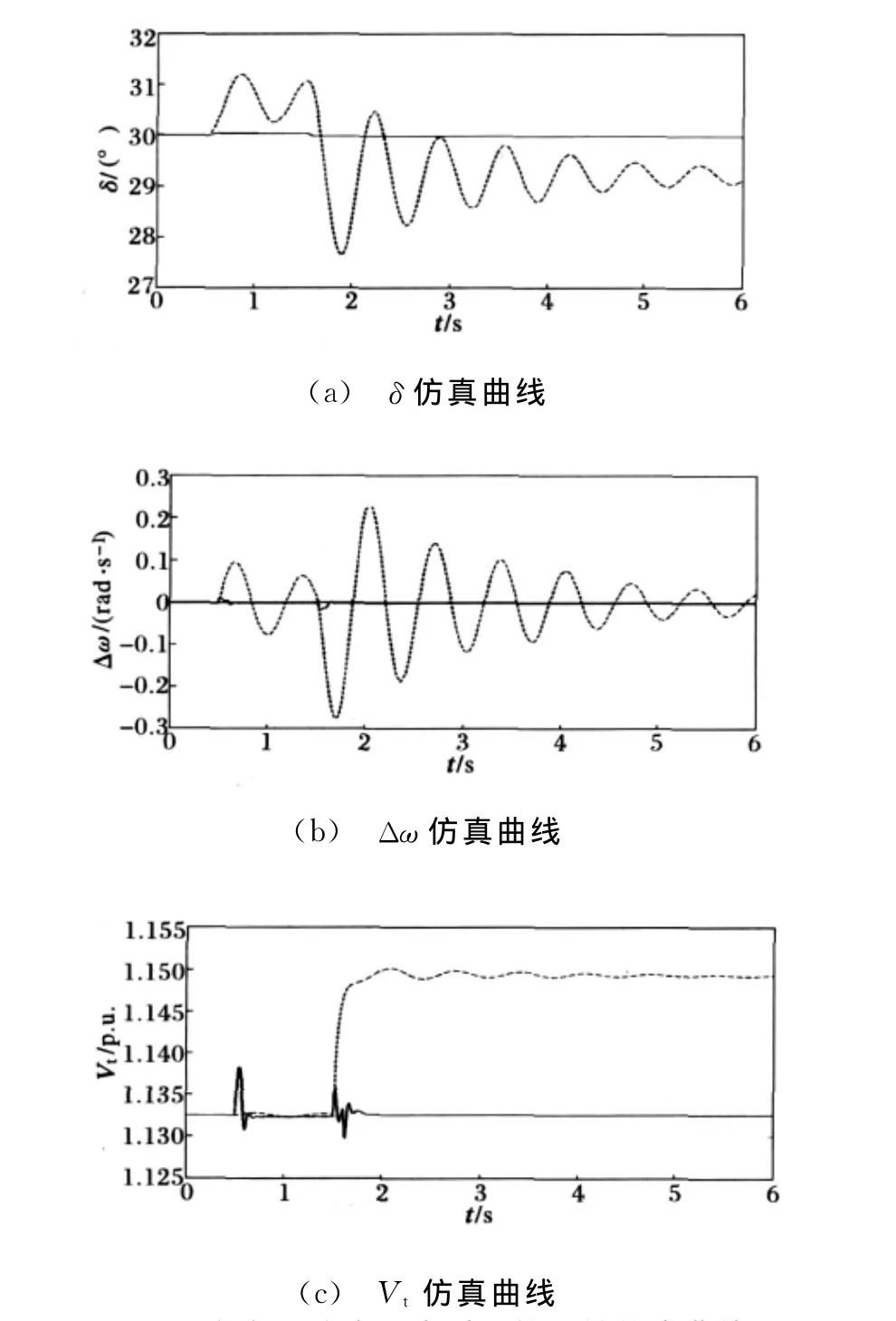
图2 存在不确定因素时下的系统仿真曲线Fig.2 System simulation curves under the uncertain factors

（2）系统在0.5 s时同时出现干扰ε1、ε2，在1 s时发电机出线高压侧发生三相短路，0.15 s后短路被切除并重合闸成功，系统有关状态量的动态响应曲线由图3给出。实线为鲁棒自适应励磁控制器的系统响应，虚线为PID励磁控制器的系统响应曲线。

由图2可见，常规PID控制时系统在干扰下功角偏离稳态值，且由于参数不确定，机械振荡长时间难以平息，机端电压无法短时间恢复。而鲁棒自适应控制器在外界干扰下表现出很好的干扰抑制效果，并对不确定参数具有适应能力，各状态量很快回到稳态值，系统继续保持稳态运行。

图3所示不确定因素存在下的暂态过程中，鲁棒自适应控制器能更快地平息机组的机械震荡，使功角和转速尽快回到稳态值；在短路发生时能更有效地维持机端电压并使其快速恢复。可见，无论是稳态还是暂态过程，在所设计控制器作用下，单机无穷大系统对干扰都表现出较强的鲁棒性，对不确定参数具有自适应能力。

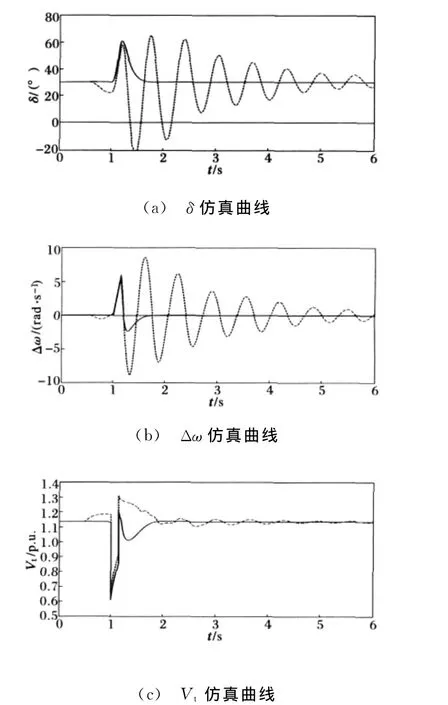
图3 三相短路扰动时的系统仿真曲线Fig.3 System simuation curves under the distrubance of three－phase short－circuit

4 结论

本文综合考虑单机无穷大电力系统多种不确定因素，针对干扰输入，通过配置系统合适的能量存储函数使得系统对干扰满足γ耗散性，进而获得L2增益干扰抑制控制器；存储函数的获得基于Backstepping技术，在递归构造存储函数过程中用估计值代替阻尼系数，使得控制律对不确定参数具有自适应能力。

单机无穷大电力系统的仿真证明了本文提出的控制律的鲁棒性和自适应性。设计过程不需要线性化处理，可以对此类不确定非线性系统具有很好的控制效果。

［1］ 孙元章，焦晓红，申铁龙.电力系统非线性鲁棒控制［M］.北京：清华大学出版社，2007.

［2］ 张春朋，林飞，宋文超，等（Zhang Chunpeng，Lin Fei，Song Wenchao，et al）.基于直接反馈线性化的异步电动机非线性控制（Nonlinear control of induction motors based on direct feedback linearization）［J］.中国电机工程学报（Proceedings of the CSEE），2003，23（2）：99－102，107.

［3］ 崔洪亮，李啸骢，左江林，等（Cui Hongliang，Li Xiaocong，Zuo Jianglin，et al）.发电机励磁与汽门控制系统的镇定性分析（Stabilizability analysis of excitation and steam－valve control system of generator）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（3）：20－24，117.

［4］ 张靠社，杨宝杰，滕夏晨（Zhang Kaoshe，Yang Baojie，Teng Xiachen）.SVC与发电机励磁鲁棒非线性协调控制（Robust nonlinear coordinated control for SVC and generator excitation）［J］.西安理工大学学报（Journal of Xi′an University of Technology），2009，25（2）：193－196.

［5］ Liao Teh－Lu.Design of an adaptive nonlinear controller to improve stabilization of power system［J］.International Journal of Electric Power and Energy System，1999，21（6）：433－441.

［6］ 孙元章，刘前进，杨新林.非线性控制中的增益和无源化方法（第2版）［M］.北京：清华大学出版社，2002.

［7］ 王宝华，张强，杨成梧，等（Wang Baohua，Zhang Qiang，Yang Chengwu，et al）.电力系统混沌振荡的自适应Backstepping控制（Chaotic oscillation control of electric power system based on adaptive backstepping）［J］.电力自动化设备（Electric Power Automation Equipment），2003，23（11）：9－12.

［8］ 付俊，赵军（Fu Jun，Zhao Jun）.基于扩展自适应Backstepping设计的TCSC非线性控制的新方法（A new method based on extended adaptive backstepping for nonlinear control of TCSC）［J］.控制理论与应用（Control Thery ＆Applications），2006，23（3）：355－361.

［9］ Lu Qiang，Mei shengwei.Recursive design of nonlinear excitation controller［J］.Science in China（Series E），2000，43（1）：23－31.

［10］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2003.