基于模糊免疫算法的汽轮发电机组OPC控制①

邓 婧，李兴源，魏 巍

（四川大学电气信息学院，成都 610065）

超速保护器OPC（overspeed protection controller）是数字式电气液压DEH（digital electric hydraulic）调节系统的重要组成部分。保证热动系统（汽轮机及调速系统）处于安全稳定的运行状态是机组超速保护的目标。当OPC的转速是额定转速的103%时，通过快速关闭调节汽阀可实现对机组的超速保护［1］。在单一故障模式下，通常根据OPC所在电网的情况灵活整定OPC的动作特性［2］，但OPC控制策略的正确性需要在实际电网事故中进行校验［3］。发电机组并网运行时，如果OPC控制策略选择不当，不仅无法实现超速保护，而且会使汽门频繁开关，产生“乓乓”现象，给机组轴系和热力系统造成频繁冲击，严重影响机组安全，甚至可能使电网大规模地甩负荷，发生频率振荡或频率失稳事故，最终造成整个电网崩溃。

在电站汽轮机调速系统中常常包括时滞、惯性、干扰、死区和饱和等非线性环节［3］。模糊控制由于无需知道被控制对像的数学模型，具有较强的鲁棒性等特点，广泛应用于难于获得精确数学模型、非线性和大滞后系统的控制。

生物免疫系统具有独特的识别机制、强大的自适应和记忆功能，已在国内外引起了广泛的重视。许多领域的科研人员对生物免疫系统中蕴含的机制和功能进行了深人研究，期望从中找到解决实际问题的方法。适应性免疫应答过程中T细胞具有促进和抑制两种作用，能保证免疫系统获得较快的响应速度和足够的稳定性，这种调节机制可用来有效改进控制系统的性能［4～6］。

在以往的模糊控制器设计中，通常的控制准则是离线整定，其缺点是不能修改，适应性较差。本文在OPC动作引起系统振荡的机理分析基础上，结合模糊控制的原理实现对OPC动作逻辑的修改，并通过免疫算法结合国际通行的NETOMAC仿真软件分析得到的模糊控制规则对其控制规则进行自适应整定从而抑制系统的振荡，实际系统的仿真论证了该OPC附加控制的效果。

1 OPC振荡机理分析

1.1 OPC模型

DEH的保护系统OPC功能设定为转速达到103%n0时快关中压调节汽阀；在n0×103%＜n＜n0×110%时，超速控制系统通过OPC电磁阀快关高、中压调节汽阀，实现对机组的超速保护［7～10］。

OPC的简单动作特性如图1所示［11］。可知OPC实现的是典型的开环控制快关快开规律。

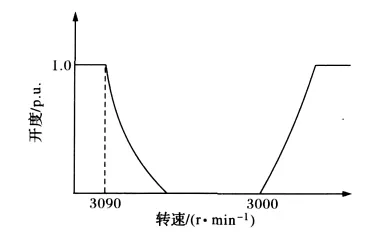
图1 OPC简单动作特性图Fig.1 Simple operating characteristics of OPC

OPC的基本动作描述如下：

通过逻辑电路控制调速和OPC动作的选择，即当指令条件不满足，OPC不动作时控制通路保持调速器调节，由调速器的调频环节进行跟踪调节；当指令条件达到，屏蔽调速器，控制通路转到OPC逻辑，完全由OPC进行控制阀门。OPC的动作逻辑简单类似于一个由转速整定的二值电平控制模型，即转速升至3090 r／min，由执行机构动作，汽门全关；转速降至3000 r／min，由执行机构动作，阀门全开。

1.2 OPC振荡机理分析

图2表示OPC动作后系统的频率振荡，假如在t＝0时，负荷突减，机组功率过剩，转速上升。若一次调频能力不足，转速上升至3090 r／min，OPC动作，全占阀门控制，关闭高压调节门和中压调节门，转速降低至3000 r／min，OPC动作全开阀门，由于存在惯性和时滞，机组转组继续下降，如果OPC的控制策略不当，有可能会下降至低频减载的动作值，从而使转速重新升高至OPC的动作值，如此造成系统频率振荡。

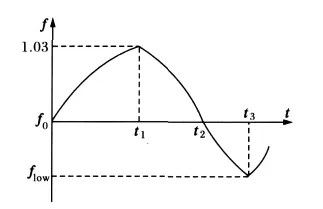
图2 OPC动作下的频率动态Fig.2 Frequency dynamics of OPC when operating

1.3 OPC动作特性的修改

如图1所示，OPC的动作是一个数字控制器，其动作逻辑是可以修改和整定的，见图3，修改后的OPC动作特性中可以人为调整的参数有：

（1）上升阶段和下降阶段采取的控制策略；

（2）汽门最小开度x1；

（3）汽门最终开度x2；

（4）汽门关闭时间tno。

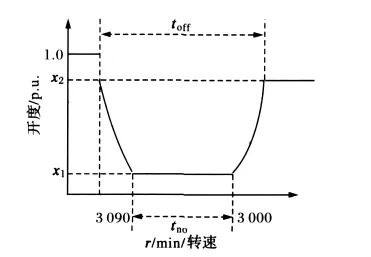
图3 修改后的OPC动作特性图Fig.3 Simple operating characteristics of OPC after the revision

2 模糊免疫控制原理

模糊控制是建立在人类思维具有模糊逻辑特性的基础上的。其控制核心是在于它用具有模糊性的语言条件语句，作为控制规则去执行控制。但模糊控制规则存在精度不高，自适应能力有限和易产生振荡现象等问题，使模糊控制器的应用场合受到了很大限制。免疫是生物体的一种特性生理反应。生物的免疫系统对于外来侵犯的抗原，可产生相应的抗体来抵御。抗原和抗体结合后会产生一系列的反应，通过吞噬作用或产生特殊酶的作用而毁坏抗原。通过免疫控制的反馈机理对模糊控制规则的加权函数进行自适应调整，可在保持控制本身优点的同时，也提高模糊控制的精度。

生物的免疫系统由淋巴细胞和抗体分子组成，淋巴细胞又由胸腺产生的T细胞（分别为辅助细胞TH和抑制细胞TS）和骨髓产生的B细胞组成，当抗原侵入机体并经过周围细胞消化后，将信息传递给T细胞，即传递给TH和TS细胞，然后刺激B细胞，B细胞产生抗体以消除抗原。当抗原较多时，机体内的TH细胞也较多，而TS细胞却较少，从而会产生较多的B细胞。随着抗原的减少，体内TS细胞增多，它抑制了TH细胞的产生，而B细胞也随着减少［12～14］反馈系统便趋于平衡。抑制机理和主反馈机理之间的相互协作，是通过免疫反馈机理对抗原的快速反应和稳定免疫系统完成的［15］，见图4。

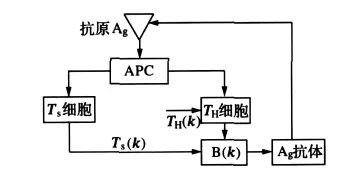
图4 体液免疫响应过程示意图Fig.4 Diagram of humoral immune respone process

生物信息系统的这些智能行为，为科学和工程领域提供了各种理论参考和技术方法。基于上述免疫反馈原理，各个领域的专家学者提出了多种免疫控制算法。比较典型一种的是模糊免疫控制算法：假设第k代的抗原数量为ε（k），由抗原刺激的TH细胞的输出为TH（k），TS细胞对B细胞的影响为TS（k），则B细胞接收的总刺激为

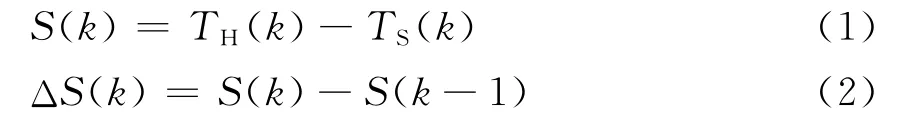
其中TH（k）＝k1ε（K）

TS（k）＝k2f（S（k），ΔS（k））ε（k）

若以抗原的数量ε（k）作为偏差e（k），B细胞接收的总刺激S（k）作为控制输入u（k），则有

本文采用上述模糊免疫反馈原理所设计的OPC附加控制器中的控制规则加权函数α（t）随控制器输出的变化而变化，具备自适应的功能。

由此，得到如下的反馈控制规律

其中kp1＝K（1－ηf（u（k），Δu（k））），K＝k1，K为控制反应速度，

3 贵阳南部电网和OPC动作过程

事故前，贵阳南部电网发电出力为1050 MW，负荷为917 MW，通过青岩变向500 k V系统上网86 MW。事故中，解网后，贵阳南部电网因功率过剩，造成频率上升，约5 s时上升到最高频率（记录到的最高频率为51.44 Hz），尔后下降至最低频率（46.47 Hz），随后出现多次大幅波动，机组有功也在波动。

贵阳电厂8号和9号机组因机组过速跳闸保护（3100 r／min、0”关主汽门，机组跳闸）动作而造成机组跳闸。清镇电厂7号和8号机组因机组过速保护OPC（3090 r／min、0”关调节汽门，机组不跳闸）动作造成功率波动，关闭调节汽门，7号机组功率的波动从200 MW降至0后，由于OPC保护在电网频率降至50 Hz以下时，OPC返回，全打开调节汽门，造成功率又上升至200 MW，电网频率上升至51.5 Hz，OPC又动作，机组调节汽门全关，功率的波动又从200 MW降至0，共重复19次。由于8号机组OPC动作后，8号机组机调节汽门的开度置为0，故在OPC第一次动作关闭调节汽门后，8号机组功率的波动从200 MW降至0后，由于OPC保护在电网频率降至50 Hz以下时，OPC返回，不打开调节汽门，功率仅在0到20 MW间波动，共波动12次，直至逆功率保护动作，＃8机跳闸。

图5 贵阳南部电网故障前接线方式Fig.5 Connection mode of guiyang southern power grid before the fault

4 OPC附加模糊控制器的设计

本文所设计的OPC附加模糊控制器结构如图6所示。

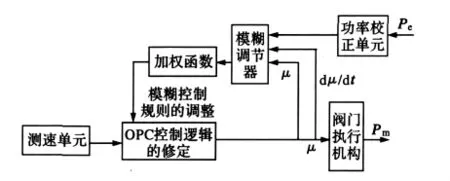
图6 OPC附加模糊控制器Fig.6 Fuzzy controller added to OPC

从OPC的动作条件及其引起系统振荡机理分析可知，对OPC的控制信号中频率变化和功率变化同等重要，因此本文在设计OPC的附加控制时，将频率变化及频率变化率同时作为模糊控制器的输入，而功率变化信号对OPC的控制作用则体现在对控制规则加权函数α（t）的修正上，这样既避免了模糊控制器输入量导致的规则维数灾，又可以在OPC的控制中同时计及频率和功率的影响，更好地反馈系统的状态。

在实际功频电液调节系统中，本应测取汽轮机的实发功率，由于技术上的困难而采用了用发电机功率代替汽轮机功率。但由此而带来的问题是反调现象的产生。在本文所设计的控制器中采用了发电机功率信号对加权函数进行修正，为避免上述反调现象的产生，引入转速微分信号，把发电机功率信号校正成为汽轮机功率信号。

4.1 OPC控制逻辑修改的设计

本文通过输入频率偏差和频率偏差变化率，输出OPC的阀门控制指令，采用模糊控制原理对OPC的控制逻辑进行整定。

4.1.1 模糊控制器的输入变量和输出变量

输入变量为频率偏差E和频率偏差变化率ΔE，输出变量为阀门开度指令u。

4.1.2 输入变量和输出变量的语言描述

ΔE和u的模糊集均为

［NB，NM，NS，O，PS，PM，PB］

E的模糊集为

［NB，NM，NS，NO，PO，PS，PM，PB］

E和ΔE的论域均为［－6，6］，u的论域为［－7，7］。

4.1.3 模糊控制规则的确定

当误差较大时，选择控制量以尽快消除误差为主；而当误差较小时，选择控制量要注意防止超调，以系统的稳定性为主要出发点。

根据以上原理，得到初始控制规则如表1所示。

表1 初始模糊控制规则Tab.1 Initial fuzzy control rules

以上得出的控制规则是经离线整定得出的，不能适应外界干扰条件的变化，因此本文把控制规则数字化，把语言变量值定义为相应的整数对应的控制基［16］，选择一个带有加权因子调整控制规则的输出量解析表达式

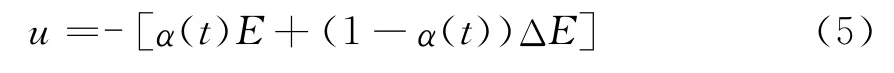
其中α（t）为调整函数，又称加权函数。

4.2 控制规则加权函数的在线调整

根据生物免疫系统的反馈规律可知免疫控制实际上是一个将比例系数采用模糊免疫调节的变比例控制，参数K控制反应速度，参数η控制稳定效果。因此，合理的调整K和η，可以使系统响应加快，超调量减小，偏差［4］。

将功率变化ΔP作为模糊调节器的抗原，输出的阀门指令u（t）作为模糊调节器的输入。则有

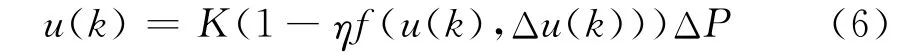
令

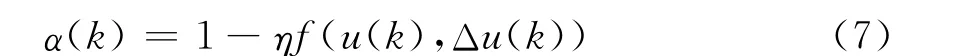
f（·）采用模糊控制规则逼近。经仿真调整后取K＝20为一固定比例系数，η为控制稳定效果调整系数，这里设置为1。

首先将输入变量u（k），Δu（k）模糊化，其基本论域分别定义为［－u，u］和［－Δu，Δu］。u的语言变量定义为NB，NM，NS，NO，PO，PS，PM，PB；Δu的语言变量定义为NB，NM，NS，PS，PM，PM，PB。描述模糊子集的隶属函数均为正态分布型隶属函数。

将对应的输出变量f（·）在（－1，＋1）区间采用正态分布型隶属函数定义为NB，NM，NS，O，PS，PM，PB。依据OPC的动作原理并经仿真实验调整，制定模糊控制规则共48条，具体内容如表2所示。

输入量u（k），Δu（k）由模糊产生器映射为模糊集合后，经模糊推理及重心法去模糊，得到确定的输出量f（·），然后代入上式，计算出α（k）。

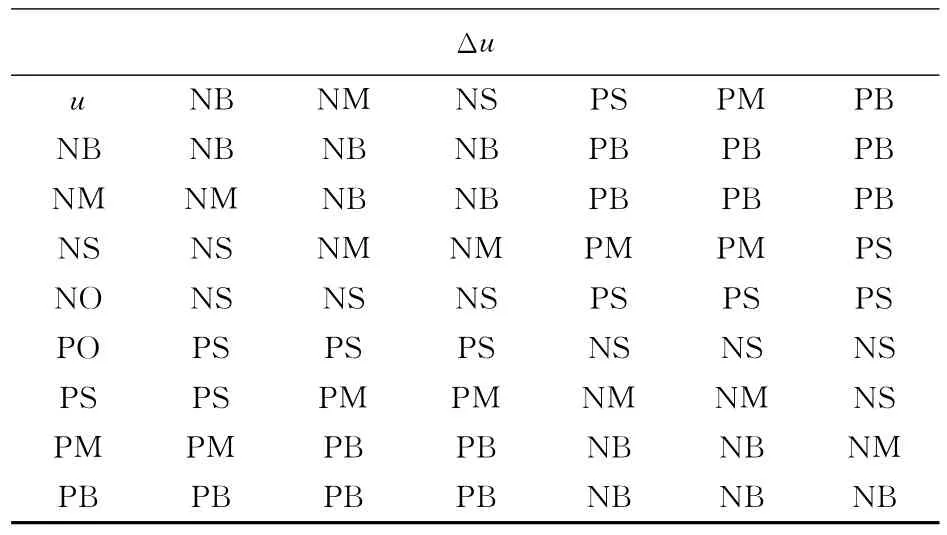
表2 加权函数的调整控制规则Tab.2 Regulation control rules of weighting function

得到控制规则的自适应调整后，可存储于OPC的控制逻辑中，实时控制时，不断根据功率变化、频率变化及其变化率进行扫描以查询控制表得到相应的控制值。

5 仿真测试及结果分析

本文利用2006－07－07贵阳南部电网故障及发生的OPC的动作过程，用NETOMAC程序建立原动机，调速器和OPC及其控制逻辑的详细模型。图7和8给出了仿真测试结果。

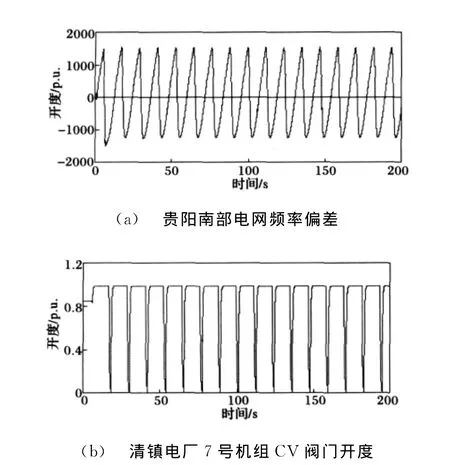
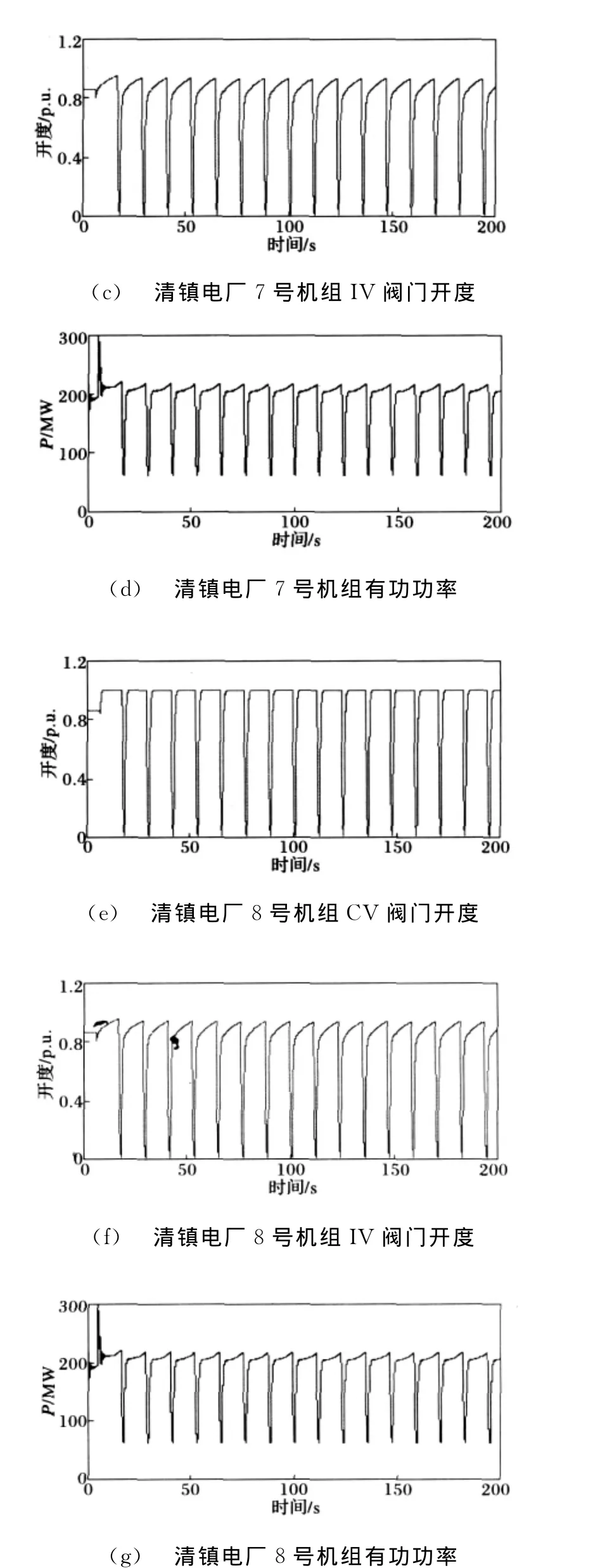
图7 未投入OPC附加模糊控制器时的仿真图Fig.7 Simulation results when not inputting the extra－OPC fuzzy controller

将本文所设计的OPC附加模糊控制器分别加入到清镇电厂7号和8号机组OPC的控制策略中，得到的结果如图8所示。

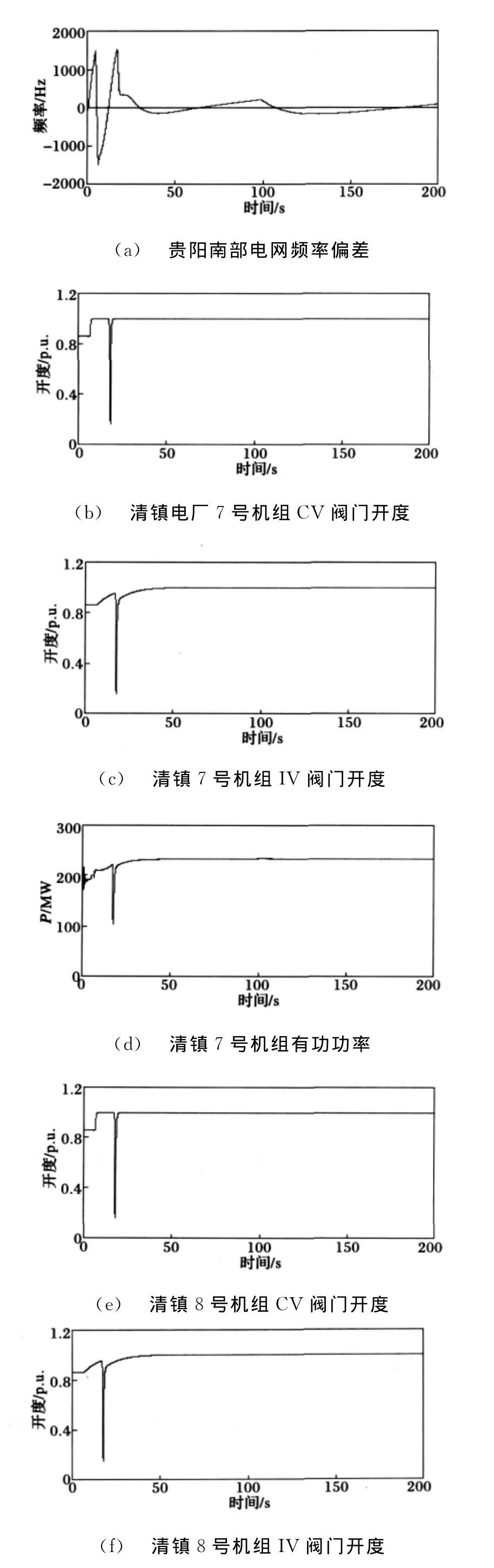
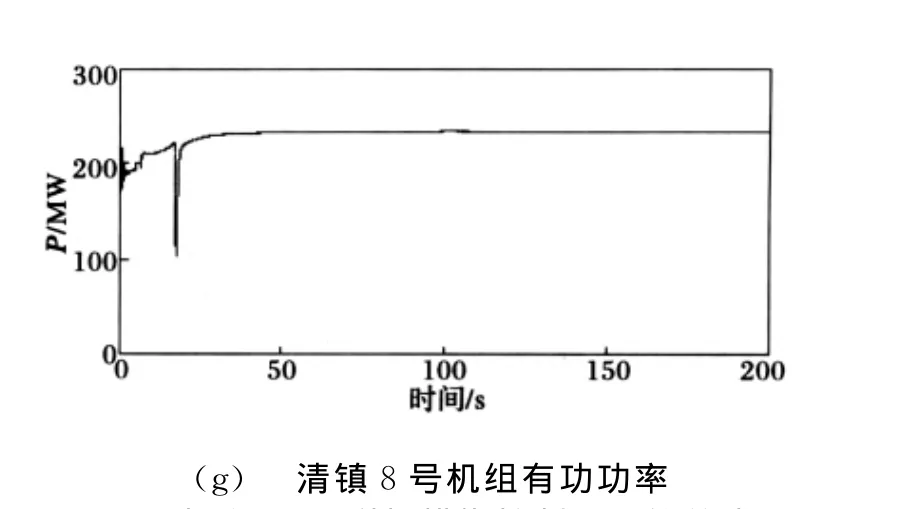
图8 投入OPC附加模糊控制器后的仿真图Fig.8 Simulation results when inputting the extra－OPC fuzzy controller

故障发生时，清镇电厂7号机组的OPC完全代替调速器对汽轮机高中压阀门进行控制，最终导致7号机组的有功功率大幅度波动，系统振荡。对实际机组的动作特性进行仿真，得到故障时未加入OPC附加模糊控制器时贵阳南部电网频率偏差、清镇电厂7、8号机组的高压阀门、中压阀门以及有功功率的结果如图7所示。

从图7和图8可以看出，采用控制规则的加权函数自适应调节的模糊控制器以后，系统不会出现切机，切负荷等情况，可以迅速稳定系统频率，较好地抑制系统振荡。

7 结论

本文基于OPC的动作原理及模糊免疫方法设计了OPC附加模糊控制器。该控制器设计方案可以有效解决汽轮机调速系统中的时滞，非线性及数学模型不易获取的难点，易于编入OPC的控制逻辑中，便于工程实现。此控制器可根据系统频率变化及频率变化率得到阀门输出指令，并根据功率的变化对控制规则加权函数进行自适应调整，具有一定的鲁棒性。通过OPC简单控制逻辑与本文所设计的控制器对比用Netomac仿真结果证明了其有效性。

［1］ 肖增弘，徐丰.汽轮机数字式电液调节系统［M］.北京：中国电力出版社，2003.

［2］ 宋铭，叶昭龙，何奉奎（Song Ming，Ye Zhaolong，He Fengkui）.纳雍发电总厂4＃300MW机组OPC功能改造（Nayong power 4＃300MW generator′s OPC function remoulding）［J］.贵州电力技术（Guizhou Power Technology），2005，77（11）：1－3.

［3］ 王爽心，姜妍，李亚光（Wang Shuangxin，Jiang Yan，Li Yaguang）.汽轮机调速系统模糊免疫PID控制的混沌优化策略（Chaos optimization strategy on fuzzy－im－mune－PID control of turbine regulating system）［J］.系统仿真学报（Journal of System Simulation），2006，18（6）：1729－1732.

［4］ 王斌，李爱平（Wang Bin，Li Aiping）.模糊免疫非线性PID控制的优化设计（Optimal design of fuzzy immune nonlinear PID control）［J］.控制工程（Control Engineering of China），2007，14（S）：81－83，95.

［5］ Perelson A S.Immune network theory［J］.Immunological Review，1989，110（8）：5－36.

［6］ 王磊，潘进，焦李成（Wang Lei，Pan Jin，Jiao Licheng）.免疫算法（The immune algorithm）［J］.电子学报（Acta Electronica Sinica），2000，28（7）：74－78.

［7］ 田丰，张俊杰（Tian Feng，Zhang Junjie）.大型机组电超速保护装置综述（Comment on over－speed protection control system of large size turbine unit）［J］.国际电力（International Electric Power For China），2001，（4）：13－18.

［8］ 张镇一，朱程滨（Zhang Zhenyi，Zhu Chengbin）.电超速保护装置的分析与评价（The analysis and evaluation of overspeed protection device）［J］.汽轮机技术（Turbine Technology），1995，37（6）：321－326.

［9］ 田丰，余天龙（Tian Feng，Yu Tianlong）.大型机组甩负荷试验若干问题的探讨（Discussion on the problems in load－rejection test of large size generating units）［J］.电力建设（Electric Power Construction），2000，33（9）：48－51.

［10］田丰，余天龙，欧坚，等（Tian Feng，Yu Tianlong，Ou Jian，et al）.珠海电厂700MW机组超速限制系统特性分析（Characteristics analysis to overspeed limiting system of 700 MW unit at Zhuhai power plant）［J］.热力发电（Thermal Power Generation），2001，（2）：46－48，58.

［11］黄宗君，晁剑，李兴源，等（Huang Zongjun，Chao Jian，Li Xingyuan，et al）.贵阳南部电网高频问题与超速保护器仿真研究（High frequency phenomenon caused by fault occurred in southern part of Guiyang power grid and simulation of overspeed protection controller）［J］.电网技术（Power System Technology），2007，31（15）：26－32.

［12］廖亦凡，刘忠，侯玉宝（Liao Yifan，Liu Zhong，Hou Yubao）.数字液压系统的模糊免疫PID控制研究（Research on fuzzy immunity PID control of digital hydraulic system）［J］.微计算机信息（Microcomputer Information），2008，24（5－1）：68－69，7.

［13］江中央，蔡自兴，龚涛（Jiang Zhongyang，Cai Zixing，Gong Tao）.一种改进的模糊免疫反馈PID控制器（An improved fuzzy immune feedback PID controller）［J］.控制工程（Control Engineering of China），2008，15（5）：485－488.

［14］吕岗（LüGang）.免疫算法及其应用研究（Study on Immune Algorithm and Its Application）［D］.北京：中国矿业大学信息与电气工程学院（Beijing：School of Information and Electrical Engineering of China University of Mining and Technology），2003.

［15］郑恩让，回立川（Zheng Enrang，Hui Lichuan）.免疫优化模糊控制及其应用（Fuzzy control with immune optimization and its application）［J］.控制工程（Control Engineering of China），2006，13（5）：460－462.

［16］周力，崔袆（Zhou Li，Cui Yi）.一种带折衷因子的FUZZY控制器的研究（Fuzzy controller with compromise factor）［J］.安徽工程科技学院学报（Journal of Anhui University of Technology and Science），2004，19（3）：37－40.