基于收益管理的BTO制造企业定价和能力规划研究
2011-04-10陈志祥
李 丽,陈志祥,史 创
LI Li1,CHEN Zhi-xiang2,SHI Chuang1
(1. 中山大学 国际商学院,广州 510275;2. 中山大学 管理学院,广州 510275)
0 引言
收益管理(YM,yield management)通常定义为“以合适的价格在合适的时间将合适的产品卖给合适的顾客”(J. I. McGill,G. J. Van Ryzin,1999),它的核心思想是通过差别价格战略、主动的能力计划和提前购买来管理需求、改进交货可靠 性(WEATHERFORD AND BODILY,1992)。YM方法已经在一些服务业得到广泛应用,但是在制造环境中的应用却非常少。实施YM策略对于服务和制造业有两个非常重要的区别:1) 非易逝库存。到目前为止,所有的YM的实施都假设库存是易逝的。在制造环境中,库存本身通常非易逝,但是制造产品库存的能力是易逝的。例如,某些产能今天不用,明天就没有用了,这一点与飞机座位非常相似;2)生产和能力。与库存问题密切相关的是生产和能力决策。在许多YM情况下,能力通常是固定的。这对于制造环境不成立,因为制造工厂不会在某个时刻停止生产,而且能力有时是一个柔性参数。因此,能力和生产需要在不同产品间分配。 正是由于制造业的生产计划期是无限的,不可能应用提前购买或报童模型等策略。
由于顾客对制造产品的交货速度、交货可靠性和订单更改响应性的要求越来越高,YM在按订单生产(BTO)模式下的制造业中有着巨大的应用潜力(Harris etal.,1995)。然而,从国内外已有文献来看,对于BTO模式下YM的研究和应用仍比较缺乏。文献Palaka,Erlebacher,and Kropp [1998]and So and Song [1998] and Ray and Jewkes (2004)基于排队理论为制造企业建立了整合交货期、能力规划和定价决策的优化模型,但是企业只服务一个细分市场。类似服务业通过提前预定来区分顾客,制造业也可以通过不同的交货期来细分顾客市场,从而达到收益最大化。Gallien,Tallec,Schoenmeyr(2004)研究了单台机器和有优先权排队系统下订单的动态控制过程,从而为这些订单制定价格、交货期决策提供依据。与他们不同的是,我们对订单进行分类,而不是单独对待每一个订单,这在实践中更容易实施。正如Holweg and Pil[2004]所建议的,要求一周内交货的顾客需要支付标价的100%,要求两周内交货的顾客支付97.5%,而能够忍受更长交货期的顾客只用支付95%。
接下来,我们将建立和分析基于YM的优化模型和无差异化模型,然后用数值算例来比较两个模型的最优决策策略和期望利润以证明制造业采取YM战略的有效性。
1 模型建立
1.1 基于YM的优化模型
我们假设一家BTO制造企业基于不同的承诺交货期(L1<L2)将顾客订单分为紧急订单(i=1)和普通订单(i=2)。订单泊松到达, 假设到达率为价格 的线性函数,即
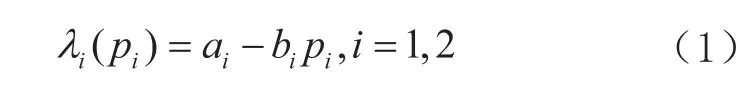
其中,ai为价格为零时的平均需求率, bi为平均需求率的价格弹性 (ai,bi>0)。
令λ12为总需求,即:

假设两类订单的可变成本为m。两类订单的加工时间均满足负指数分布,平均生产率相同,用µ表示。企业制定了一个内部交货期可靠性目标水平SR(0<SR<1),即任意订单的实际交货时间等于或小于Li的概率。如果企业不能在承诺的交货期Li内交货会给企业带来负面影响,因此企业希望这个目标越接近1越好。基于这些假设,我们可以用有优先权的M/M/1排队模型来模型企业的生产运作。因为紧急订单有优先权,因此不受普通订单的影响。紧急订单的实际交货期(在系统中的时间)l1满足负指数分布,均值为企业不能满足承诺交货期的概率为e-(µ-λ1)L1,即

我们可以将两类订单看作一个泊松流,平均到达率为λ12。因为l12肯定比l1或l2大,我们用l12代替l2以得到如下交货期保证形式 :
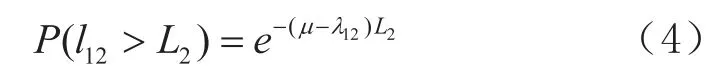
企业可以通过雇用更多的工人或购买新设备等投资来提高生产率µ。假设投资函数M(µ)是生产率µ的线性函数 [Ray and Jewkes,2004],即

其中,A是生产能力的边际成本。
因为企业的目标是单位时间的利润最大化,因此其优化模型如下
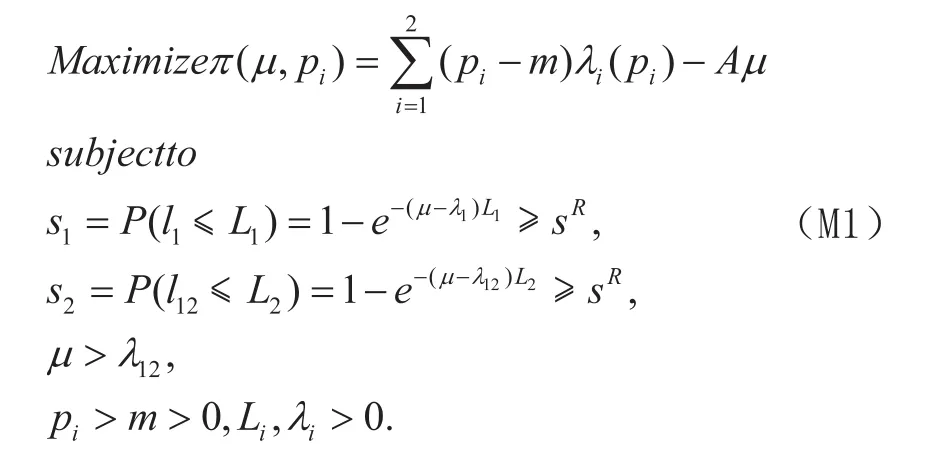
不难证明目标函数是µ的递减凹函数,为了达到最大值,交货期约束必须是有效约束。从前面两个约束条件可得最优决策值,即
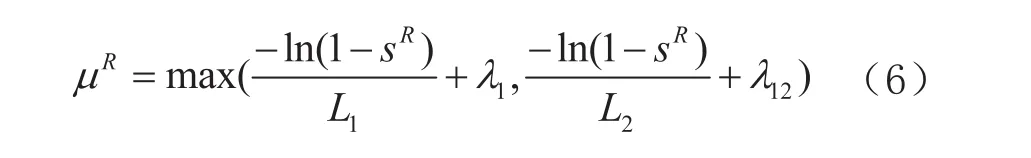
用式(6)代入 M1,可得以下两个模型:
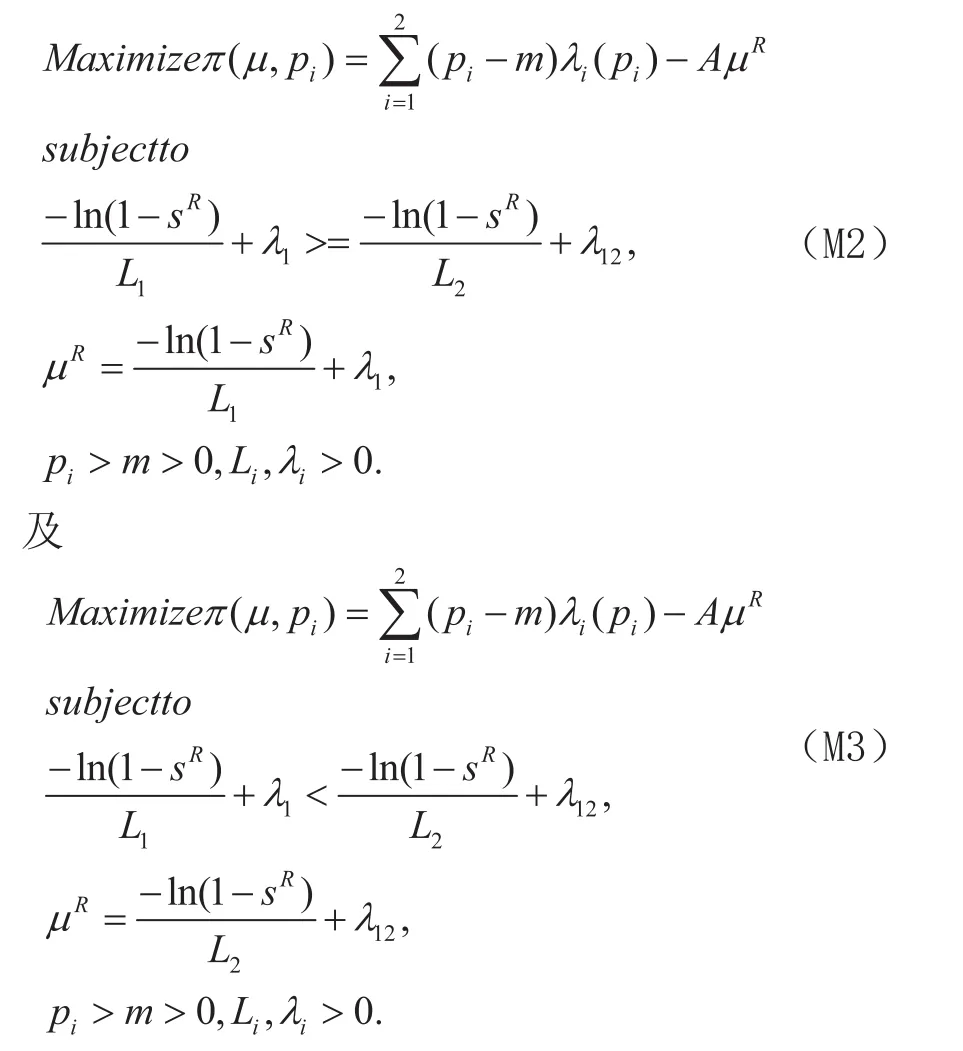
将式(1)和(2)代入M2 和 M3 ,可得以下两个模型 :

可以证明M4和 M5 的目标函数是两个独立变量p1和p2的二次凹函数。
对于M4 和 M5,
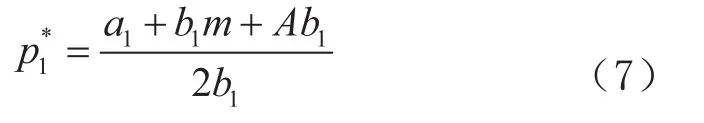
对于 M4,

1.2 无差异化模型
如果企业为两类顾客提供相同的承诺交货期,那么企业只能制定一种价格,此时的利润最大化模型可以写成如下形式:

2 数值算例
在本部分,我们用数值算例阐述在不同的需求参数下YM策略对企业利润的影响,如表1所示。对于M1,令L1=1,L2=3;对于模型M7,令L=3。原参数为a1=1000,b1=20,a2=1000,b2=40,A=10,m=5,SR=0.99。
从上表可以看出,企业采用YM策略(基于交货期对顾客进行细分)的利润高于非差异定价(同等对待所有顾客)的利润(第5行大于第7行);而且当两类需求的价格差别()越大(第4行),企业就越应该采取YM策略(第8行)。因此,当越来越多的顾客为他们的定制产品接受不同交货期时,BTO制造企业采用YM策略将大大提高利润。
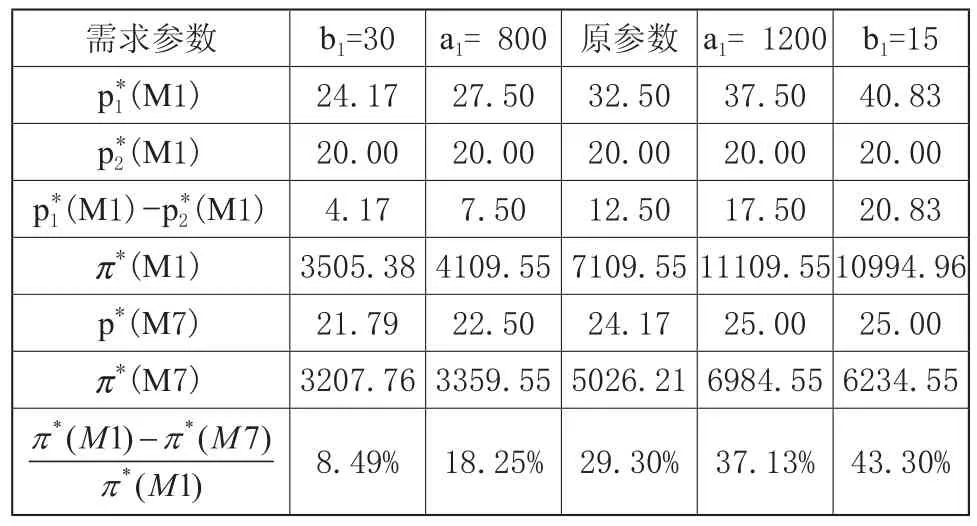
表1 需求参数对M1和M7的影响
3 结束语
在不断加剧的竞争环境下,制造企业可以采用成功应用于服务业的YM策略来提高利润。这种将定价和产能计划进行整合的策略可以更好地匹配供需,从而提高收入并降低成本。本文基于不同交货期对顾客进行细分,建立了价格和产能规划决策的利润最大化模型,并给出了数值案例分析。本文对于收入管理在制造业的理论研究及帮助BTO制造业提高利润都有重要参考价值。我们模型的一个扩展是考虑满足更一般分布的排队模型。一个更有趣的问题是考虑企业会对其他企业行为作出响应的竞争环境。
[1] M. Holweg,F. K. Pil.,“The Second Century:Reconnecting Customer and Value Chain through Build-to-Order; Moving beyond Mass and Lean Production in the Auto Industry”,The MIT Press,2004: 113-214.
[2] J. I. McGill,G. J. Van Ryzin,“Revenue management:Research overview and prospects”,Transportation Science,1999,33(2): 233-256.
[3] deB. Harris,H. Frederick,and Jonathan P. Pinder,“A revenue management approach to demand management and order booking in assemble-to-order manufacturing”,Journal of Operations Management,1995,13(4): 299-309.
[4] Kondalarao. Palaka,Steven. Erlebacher,Dean H. Kropp,“Lead-time setting,capacity utilization,and pricing decisions under lead-time dependent demand”,IIE Transactions,1998,30: 151-163.
[5] Kut C. So,and Jing-Sheng. Song,“Price,delivery time guarantees and capacity selection”,European Journal of Operational Research,1998,111: 28-49.
[6] Jeremie. Gallien,Yann Le. Tallec,Tor. Schoenmeyr,“A model for make-to-order revenue management”,Working paper,MIT Sloan School of Management,Cambridge,2004.
[7] Saibal. Ray,E. M. Jewkes,“Customer lead-time management when both demand and price are lead-time sensitive”,European Journal of Operational Research,2004,153: 769-781.
[8] Weatherford L R,Bodily S E. 1992. A taxonomy and research overview of perishable-asset revenue management:Yield management,overbooking,and pricing [J]. Operations Research,40,(5),September-October: 831-844.
