基于遗传算法的多级叶片优化排序的快速收敛研究
2011-04-10赵德胜李彩琴
赵德胜,张 雪,李彩琴
ZHAO De-sheng,ZHANG Xue,LI Cai-qin
(西安邮电学院,西安 710121)
0 引言
所谓遗传算法收敛的复杂条件,是指约束条件苛刻、可行解的可行区域狭窄的条件。降低发动机颤振故障发生的几率,对发动机压气机转子的制造、安装作出一系列的限制措施是必要的。其中,最重要的两个问题是如何控制叶片静质量矩和叶片固有频率。除了在制造时采取措施以外,在安装时降低叶片静质量矩和保证转子叶片具有合格的固有频率也是必不可少的。这就需要对叶片安装施加必要的约束条件。在复杂条件下,人工叶片排序效率很低。
利用计算机求解此类问题时,叶片排序问题被看作是一个组合优化问题。采用常规的组合优化求解叶片排序问题,算法复杂,对于某些“恶劣”的数据可能求不出正确的排序结果。遗传算法在求解组合优化问题上具有很大的优势,但是当叶片排序条件较为复杂时,收敛速度慢、甚至不能求出优化排序结果;适应度函数设计也较为困难。为解决这个问题,本文利用改进遗传算法,在此基础上进行了适应度函数设计,并采用植入种子染色体导引法和内外交换法进行排序,所得结果正确,收敛速度快。
1 叶片排序约束条件
某航空设备制造厂根据实际工作需要提出了下述叶片安装条件:
1) 整级中的每个叶片与相邻叶片应具有频率差,且各叶片频率应为一大一小锯齿型分布,不允许连续增大或减小。即为“错频”排列。
2) 在整级叶片中,其中三对叶片1~2、8~9、16~17的频率差应不小于11Hz,且应比其它的相邻叶片对的频率差高出不小于2Hz。允许这三对叶片的频率差比这三对中的任一叶片与相邻叶片的频率差高出不小于2Hz。
3) 整级叶片中,相邻的4个叶片之间的三个频率差不得完全相同。
4) 相邻叶片之间频率差应不小于6Hz,允许在互不相邻的三处,与相邻叶片频率之差不小于4Hz。
5) 整级叶片的最大频率与最小频率之差应不小于14Hz。
6) 整级叶片中的每六分之一位置(即1~4号、5~8号、9~12号、13~16号、17~20号、21~24号)上的叶片静质量矩的和之差应当不大于138g ·cm,相邻象限叶片静质量矩的和之差应当不大于115g ·cm。
7)压缩机全部叶片共分为3级,每级叶片都必须符合上述条件。为了生产率,单级叶片所提供的备选叶片数量不得大于26枚。程序运行时,一次最多可以输入100枚备选叶片,至少输出4组叶片数据。
8)非可行解可行化。如果叶片数据确实“恶劣”,有一组输出数据不是可行解。则应给出最佳备选叶片的频率和静质量矩范围(也就是如果有一组输出叶片不合格,这时,更换里面的一枚或几枚叶片,则更新后的叶片组是合格的。此时,应当给出更换叶片的频率和静质量矩的值)。
上述约束条件,给出了叶片优化排序的多个目标。为了方便求解,把3级叶片逐次求解,因此,三级叶片可以采用同一目标函数。因此,一个多目标优化问题转化为三个单目标函数求解问题。
2 单级叶片目标函数
本文的研究目标就是要求排列在180°相对位置的两片叶片的静质量矩差的绝对值之和最小,即
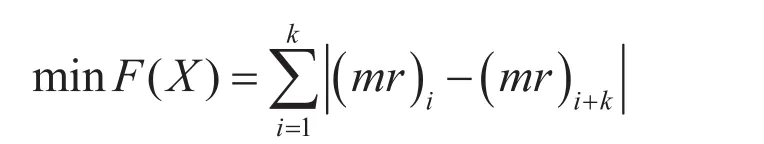
式中:k为叶片个数的一半,(mr)i为第i个叶片的静质量矩(g ·mm)。因此:目标函数设计为:

3 适应度函数设计
适应度函数的优良与否在很大程度上影响程序的收敛速度。在构造遗传算法时,处理约束条件主要有三种方法:搜索空间限定法、惩罚函数法、可行解变换法。本文采用罚函数法。本文将约束条件作为罚函数包含到适应度函数中去 ,从而将约束优化问题转换为无约束优化问题进行求解 。此时适应度函数可以写为:
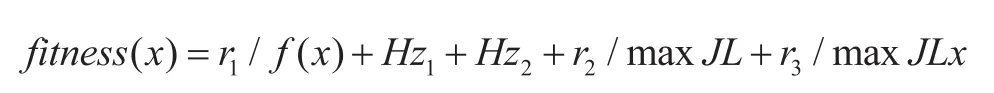
其中,r1、r2、r3、r2为罚函数尺度系数,f (x)为目标函数,Hz1为整级叶片中相邻叶片的频率差。Hz2是约束条件中(2)所允许的三对大频率差值与其他相邻叶片频率差值的频率差。
4 种群初始化
由于条件要求在100枚叶片里同时输出4组数据,因此本文把4组数据作为4条染色体,每条染色体代表一组叶片。程序同时对4组叶片优化排序。但是,在种群初始化时,一次只能产生一条染色体。这样做的结果是:最先产生的染色体把性状好的叶片挑选了,留到最后的是性状“恶劣”的叶片,这样很可能最后一组得不到可行解,造成资源浪费。为了避免这个问题,我们先来看单级叶片染色体的产生办法:
在单级叶片中,由于对1和2号位、8号和9号位、16和17号位的频率差要求严格,因此,为了加快收敛速度,在每条染色体中,本文先在原始数据中选取三个频率最大的叶片,随机放入1、9、17号位置;然后,选取三个频率最小的叶片,随机放入2、8、16号位置。这样,每一级叶片中,还有18个位置没有安放叶片。原始数据的剩余叶片,程序自动按照频率把它分成两部分,叶片频率大于平均频率的为一部分,小于平均频率的为另一部分。利用轮盘赌法按照一大一小的原则,先从大频率数据组里面随机抽取一个,再从小频率数据组里面随机抽取一个。以此类推,安装完毕一条染色体的剩余基因位置。利用同样方法,产生其他染色体。通过在种群初始化时,实施人工干扰,间接减少了排序的约束条件。
由单级叶片染色体的产生办法可知:每条染色体在挑选叶片时,总是把频率最大和最小的叶片优先选取。因此,本文在种群初始化时,先选取12枚频率最大的和12枚频率最小的叶片。在产生每一条染色体时,其关键位置的叶片都从这两组叶片里随机选取。其余叶片按照单级叶片办法产生。这样就较好的保证了最后一条染色体的叶片性状。
这样做的结果是产生了4个种群。程序同时对4个种群进行优化。
5 遗传算法编码与算子
5.1 编码方式
常用的编码方式包括二进制编码 、浮点数编码 、顺序编码 、布尔矩阵编码等 。为了调试程序的方便,本文采用十进制编码方式。本文把一级叶片中的总叶片数目(24个叶片)作为作为一条染色体,即每条染色体含有24个基因,每个基因包含一片叶片的相关信息。染色体上,第一号基因位置表示第一枚叶片安装位置。
5.2 选择算子
从适应度函数的设计上可以看出适应度大的个体优于适应度小的个体 ,这与一般遗传算法中适应度大的个体优于适应度小的个体一致,因此适于直接采用基于比例的适应度分配方法。本文采用轮盘赌选择法。
5.3 交叉算子
本文的编码方式允许一个个体的染色体编码中在不同位置出现相同的基因码,如果出现相同的基因码,则表明有两个或多个叶片的相关参数是相同的,这与实际工作情况是相符合的。本文采用多点交叉。但并非完全随机交叉。由于在种群初始化时的人为因素,每个染色体中的1~2、8~9、16~17号位置基因不能和其他位置基因交叉。
5.4 变异算子
变异算子较为简单,对个体内的基因排列按一定的变异率进行随机交换即可。同样,每个染色体中的1~2、8~9、16~17号位置基因不能和其他位置基因交换。只能相同性质的基因交换,即:1、9、17可以随机交换,2、8、16可以随机交换。
6 种子染色体
普通遗传算法程序,在多约束条件下,如果原始数据比较恶劣,容易陷入局部寻优。并且,一旦陷入局部寻优,很难跳出这个局部“陷阱”,从而影响收敛速度。为了加快收敛速度,本文采用了种子染色体导引法。即事先给定一个性状比较好的染色体作为种子,其作用是引导种群向最优点靠近。在多约束条件下,人工给出性状较好的染色体可行性不高。为了减少人工工作量,本文采用种群自动产生种子的方法。通常情况下,在程序运行时,把种群最大遗传代数作为程序循环次数。本文只设定较低的最大遗传代数。例如,设定100代,即程序循环100次。在程序初次运行时,把初始种群中适应度最大个体作为种子染色体。程序运行结束后,如果没有得到优化解,所产生的种群中适应度最大个体被用来当作下一次程序运行是的种子染色体。该种子染色体被植入下一次运行时的初始种群。通过植入种子染色体不仅能够引导种群向最优点靠近;而且,当种群遗传若干代后,种群变得过于庞大,从而影响运算速度,通过再一次种群初始化,可以有效解决这个问题。
7 内外交换法
染色体一旦产生,其交叉、变异等操作只能在染色体内部进行,不能再与外部数据进行数据交换。这不但造成剩余叶片资源浪费,也会使收敛速度变慢。本文用内外交换法解决了这个问题。即:在一个种群里,随机选取一条染色体。计算它的频率差和单元静质量矩之和等相关参数。如果叶片静质量矩的和之差大于138g.cm,或相邻象限叶片静质量矩的和之差大于115g.cm,则查找出静质量矩之和大的单元;然后,在这个单元里,查找一枚静质量矩最大的叶片,并记为big。此时,原始数据的剩余叶片里,查找一枚叶片,其静质量矩比big要小,并且其频率在代替big的频率后,新的频率差应符合上述约束条件;或者与big的频率相等。同样,查找一枚静质量矩最小的叶片,并记为small。在原始数据的剩余叶片里,查找一枚叶片,其静质量矩比small要大,在代替small后,其频率要求同上。实践证明,这种方法对解决陷入局部最优解问题行之有效。
8 非可行解可行化
如果有非可行解问题,则用虚拟叶片片法解决非可行解寻优问题。在初次种群初始化时,每枚叶片都是随机选取,并且只能选取一次。对非可行解叶片组,允许部分叶片可重复选取,等于增加了叶片数量。得到可行解后,有个别叶片在染色体里出现了两次。则该叶片参数即为待更新叶片的参数。
9 实例验证
给定一组叶片原始数据如表1所示。(因篇幅限制,只给出一组数据)。
在没有种子染色体引导和没有利用内外交换法的情况下,普通遗传算法,程序循环运行了25分钟,没有得出正确结果。在有种子染色体引导和利用内外交换法时,程序循环运行20分钟,得出正确结果如表2所示。

表1 原始数据

表2 运行结果
10 结论
程序运行结果表明:在多约束条件下,该程序收敛速度大为加快,并且运行结果正确。同时,以上算例证明,改进遗传算法在多约束和原始数据恶劣条件下,利用种子引导法和内外交换法并在种群初始化时施加人工干扰使程序收敛速度较快,结果准确。用此方法编制的程序实用性强。能有效解决在复杂条件下的多级叶片排序问题。
[1] 杨训. 基于遗传算法的转子叶片优化排序[J]. 计算机仿真,2008,25(11).YANG Xun Optimum Arrangement of Rotor Blade Based on Genetic Algorithms[J].simmulink of Computer 2008,25(11).
[2] 彭国华. 混合遗传算法在叶片排序问题中的应用[J]. 西南民族大学学报,32.PENG Gguohua Application of hybrid genetic algorithm in blade arrangement of engine[J]. 32.
[3] DeJong Ka An Analysis of the Behavior of a Class of Gentic Adaptive Systems[J].Dissertion Abstracts International,1975(10).
[4] Back T,Schwefel H P.An Over View of Evolutionary Algorithms for Paramater Optimization[J].Evolutionary Computation,1999(1).
