一种基于结构函数的系统等价简化的方法

李 霞，侯 兵，侯雪梅

LI Xia1,HOU Bing2,HOU Xue-mei3

（1. 河南财经政法大学 统计系，郑州 450002；2. 华北水利水电学院 数学与信息科学学院，郑州 450011；3. 解放军信息工程大学 理学院 电子系，郑州 450001）

0 引言

系统是由一些基本部件组成的完成某种指定功能的整体，系统的概念是相对的，例如一个核电站可以看成一个系统，而其中的安全保护装置看成它的一个部件，但是如果单独研究安全保护装置，则它又可以看成一个系统。

系统部件之间的组合形式是多种多样的，可以是并联、串联或者其它一些复杂的组合形式。很多情况下，总假定系统的部件之间是相互独立的，现实中，部件之间往往是不独立的，而Copula作为一种刻画随机变量之间相依性的方法，近几年受到许多统计学者的关注.它的出现使随机变量之间的相依性刻画逐渐趋于完善，Copula理论不仅可以用于概率、统计和随机过程中，而且它在其它领域应用也非常广泛.这里就是在新的结构函数定义[1]基础上，将Copula方法应用到系统结构的研究当中去。

1 背景知识

对于一个系统，首先关注的是它的结构，在可靠性理论中，从0和1两个状态出发给出了系统结构函数的定义。

定义1.1[2]：对任意的结构向量x={x1,x2,...,xn}，其中xi表示各部件所处的状态，取值分别为0和1，若用ξ(x)记系统的状态，则它是{0,1}n→{0,1}上的一个函数，并称为系统的结构函数.

由定义，系统的结构函数ξ(x)是连接系统状态和部件状态的一个函数.在定义中，只涉及到正常和失效两种状态，失效是一种最简单的状态。若系统失效，则系统的可靠度以及累积失效率都为0；但若系统正常，此时只知道系统的状态为1，而可靠度以及累积失效率这些表征系统的量却无从知晓，为了全面描述系统所处的状态，文献[1]中从累积失效率出发引出了系统结构函数的另一种定义。

定义1.2[1]：若一个系统在 时刻的累积失效率λ(t)可以用

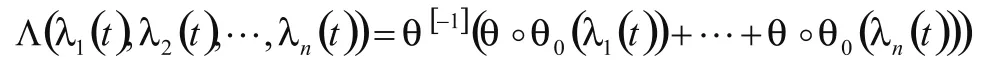
表示出来，则这样的系统称为阿基米德单调结构系统，其中Λ(λ1(t),λ2(t),...,λn(t))称为系统的结构函数，λi(t),i=1,2,...,n表示各部件在t时刻的累积失效率；θ(t)是[0,+∞)→(-∞,+∞)上的连续减函数，称为结构函数的生成元；θ[-1](t)为θ(t)的伪-逆，θ0(t)是[0,+∞]→[0,+∞)上的连续增函数，并称θ0(t)为θ(t)的伴随函数。

由定义，系统的结构函数Λ(λ1(t),λ2(t),...,λn(t))是连接部件的累积失效率和系统累积失效率的一个函数，一个系统或部件在不同时刻的累积失效率一般不同，因此，可以用累积失效率描述系统或部件在不同时刻所处的状态，而Λ(λ1(t),λ2(t),...,λn(t))则可以认为是连接部件状态和系统状态的一个函数，系统不同，其连接函数肯定不同，定义中给出了一种特殊的连接形式，并把可以用这种形式来连接的系统称为阿基米德单调结构系统。

copula的概念是sklar在1959年回答M.Frechet关于多维分布函数和低维边缘之间关系的问题时首次被引入的.

何谓copula？ copula是连接多维分布函数和一维边缘分布函数的函数。换句话说，copula是一个多维分布函数，并且其边缘分布函数是服从(0,1)区间上的均匀分布的。

定义1.3[3]：copula是一个[0,1]2→[0,1]的函数，且满足

1）C(u,0)=C(0,v)=0，C(u,1)=u，C(1,v)=v

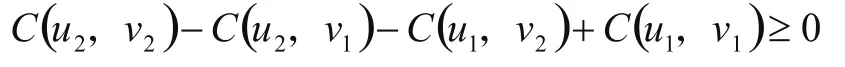
可以验证copula是一个定义在[0,1]×[0,1]上的二维分布函数，其边缘分布是[0,1]上的均匀分布。对于多维的可类似推广得到。

1941年，Widder给出了完全单调函数的定义.

定义1.4[4]：函数f(x)在它的定义域中是完全单调的，如果它满足：

1）f(x)的任意阶导数都存在；

2）f(x)的所有阶导数符号依次发生改变.

在此定义基础上，Schweizer and Sklar引出了一个生成元φ(t)能生成任意维Copula的充分必要条件。

定理1.1[5]：设φ是[0,1]→[0,+∞)上连续严格降函数，即φ(0)=+∞，φ(1)=0，用φ-1表示φ的逆函数，若Cn=φ-1(φ(u1)+φ(u2)+...+φ(un))是[0,1]n→[0,1]上函数，则Cn对任意的n≥2都为Copula的充分必要条件是φ-1在 [0,+∞]上是完全单调的。

实际中所用到的Copula维数一般都是确定的，因此下面定理更为常用。

定理1.2[6]：设φ(t)是[0,1]→[0,+∞)上连续降函数，且φ(1)=0，用φ[-1](t)表示φ(t)的伪-逆函数，若φ[-1](t)的m阶导数存在，且符号发生改变，即对所有k=0,1,2,...,m，则此时称φ[-1](t)在[0,+∞)是m-单调的，且Cn=φ[-1](φ(u1)+φ(u2)+...+φ(un))对于所有2≤n≤m是一个Copula。

定理中，由φ[-1](t)所生成的CopulaCn=φ[-1](φ(u1)+φ(u2)+...+φ(un))被称为阿基米德Copula.这里只给出二维阿基米德Copula的定义。

定义1.5[7]：设φ(t)是[0,1]→[0,+∞]上的连续、严格降的凸函数，且φ(t)=0，设φ[-1](t)是φ(t)的伪-逆函数，则C(u,v)=φ[-1](φ(u)+φ(v))被称为阿基米德Copula。其中φ(t)被称为Copula C的生成元，特殊地，若φ(0)=∞，则φ(t)称为严格生成元，这种情况下φ[-1](t)=φ-1(t)，且C(u,v)=φ[-1](φ(u)+φ(v))被称为严格的阿基米德Copula。

本文利用定义1.2中提出的结构函数的定义并结合copula的有关性质给出了一种系统等价简化的方法，为系统的研究提供了基础。

2 主要结果

定义2.1：设Λ1(t)、Λ2(t)分别表示系统L1和L2在 t时刻的累积失效率，若对任意t∈[a,b]，其中0≤a〈b≤+∞，都有Λ1(t)=Λ2(t)，则称系统L1和L2在时刻a与时刻b之间是等价的.

定理2.1：设系统L是一个阿基米德单调结构系统，即系统在t时刻的累积失效率为λ(t)=θ[-1](θοθ0(λ1(t))+θοθ0(λ2(t))+θοθ0(λn(t)))，假设θ0(t)是[0,+∞)→[0,+∞)上严格增函数，1）设f(t)=-1n(1-t)，若(θοf(t))[-1]在[0,+∞)上是n-单调的，θ(t)是 [0,+∞)→[0,+∞)上单调减函数，且θ(+∞)=0，则此系统可等价为一个n个部件所组成的并联系统；2）设g(t)=-1n(t)，若(-θοg(t))[-1]在[0,+∞)上是n-单调的，θ(t)是[0,+∞)→(0,+∞]上单调减函数，且θ(0)=0，则此系统可等价为一个n个部件所组成的串联系统.

证明：设系统中各部件的寿命分布函数分别为Fi(t)=1-e-λi(t)，且令λ'i(t)=θ0(λi(t))，F'i(t)=-1-e-λi'(t)=1-e-θ0(λi(t))=1-e-θ0(-1n(1-Fi(t)))，这里i=1,2,...,n。由于θ0(t)是[0,+∞)→[0,+∞)上的严格增函数，则Fi'(0)=0，Fi'(+∞)=1，且Fi'(t)在[0,1]上是非降函数，因此Fi'(t)是一个分布函数.这样系统的结构函数可以改写为λ(t)=θ[-1](θλi'(t))+...+θ(λn'(t)))（*）

1）由已知θ(t)是[0,+∞)→[0,+∞)上单调减函数，且θ(+∞)=0，令φ(t)=θ(-1n(1-t))，则φ(t)是[0,1]→[0,+∞)上减函数，且φ(1)=φ(+∞)=0，由θ(t)=φ(1-e-1)得θ[-1](t)=-1n(1-φ[-1](t))。把θ(t)=φ(1-e-1)以及θ[-1](t)=-1n(1-φ[-1](t))代入（*）式得

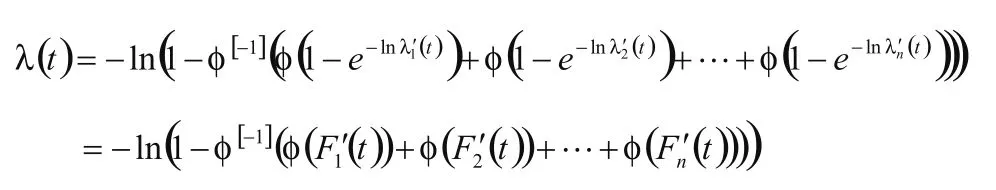
由已知(θοf(t))[-1]，其中f(t)=-1n(1-t)是n-单调的，故φ[-1](t)是n-单调的，又由1中定理1.1可知φ[-1](φF1'(t))+φ(F2'(t))+...+φ(Fn'(t)))可构造出一个n维Copula Cn，则λ(t)=-1n(1-Cn(F1'(t),F2'(t)+...+Fn'(t)))。

现给出另一系统L'，假若此系统由n个部件并联而成，n个部件的寿命分别用Xi表示，寿命分布函数分别用F'i(t)表示，i=1,2,...,n，若n个部件寿命之间具有Copula Cn，则系统L'在t时刻累积失效率为：

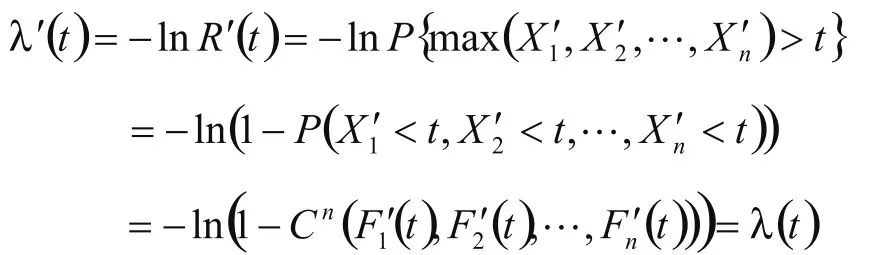
故系统L和系统L'等价，其中L'是部件寿命之间具有Cn的并联系统.

2）θ(t)是[0,+∞)→(-∞,0]上单调减函数且θ(0)=0，令φ(t)=-θ(-1nt)，则φ(t)是[0,1]→[0,+∞]上减函数，且φ(t)=0，由θ(t)=-φ(e-t)得θ[-1](t)=-1nφ[-1](-t)，把θ(t)=-φ(e-t)以及θ[-1](t)=-1nφ[-1](-t)代入（*）式得

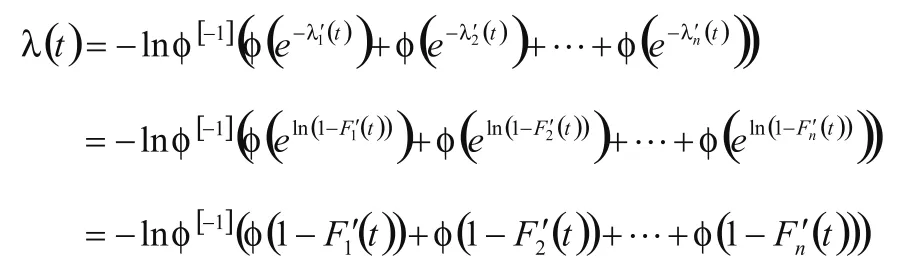
由已知(-θοg(t))-1，其中g(t)=-1n(t)是n-单调的，故θ[-1](t)是n-单调的。又由1中定理1.1可知φ[-1](φF1'(t))+φ(F2'(t))+...+φ(Fn'(t)))可构造出一个n维Copula Cn，λ(t)=-1nCn(1-F1'(t),1-F2'(t)...1-Fn'(t))

现给出另一系统L'，此系统由n个部件串联而成，且n个部件的寿命分别用Xi表示，寿命分布函数分别用Fi'(t)表示，i=1,2,...,n，若n个部件寿命之间具有（表示Cn的生存Copula[7]），则系统 L'在t时刻累积失效率为：

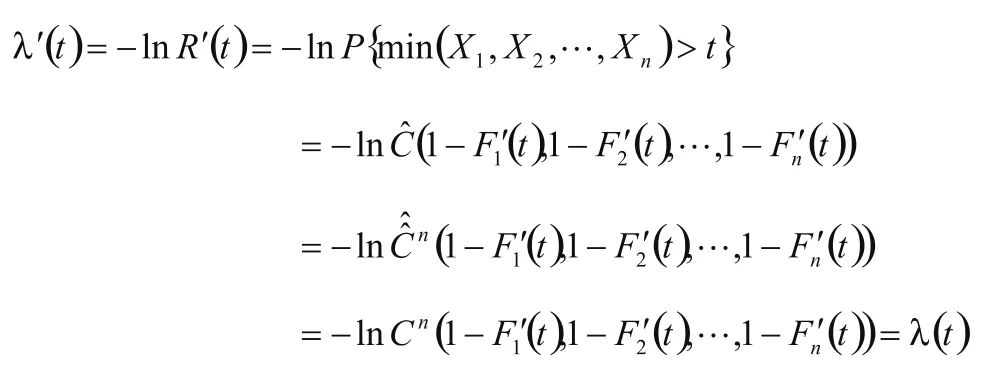
故系统L和系统L'等价，其中L'是n个部件串联所组成的系统，且部件寿命之间具有其中Cn是一个n-维Copula.

3 应用

命题3.1：由nm个独立部件所构成的串-并联系统L中，若每个并联子系统中部件个数都是n，且m个子系统中所有部件的寿命分布分别对应相同，即Fij(t)=Fj(t)，i=1,2,...,m；i=1,2,...,n现验证此类系统在某种情况下可等价为一个并联系统.

证明：由于系统L是阿基米德单调结构系统，即系统L在t时刻累积失效率为：

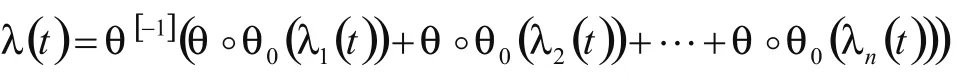
这里不妨设m=2，下面验证ξ(t)=1-(1-e-t)2是n-单调的。

由ξ(t)=1-(1-e-t)2=2e-t-e-2t，则ξ'(t)=-2e-t(1-e-t)，ξ''(t)=2e-t(1-2e-t) ，ξ'''(t)=-2e-t(1-22e-t),… ,ξ(n)(t)=(-1)n2e-t(1-2n-1e-t)。

若要保证ξ(t)是n-单调的，需1-2n-1e-t≥0，即t≥(n-1)1n2。故当t∈[(n-1)1n2,+∞]时，由2n个独立部件所构成的串-并联系统和另一并联系统等价。

说明：

1）在串-并联系统中，每个并联子系统部件个数都是n，且两个子系统中所有部件寿命分布分别对应相同，另外，n个部件之间是相互独立的.

2）等价后的并联系统中，每个部件寿命的分布函数和串-并联系统中部件的寿命分布函数存在关系并且并联系统中， n个部件寿命之间具有其中Cn是由所生成的 维Copula。

利用同样方法，可以验证m取其它值的情况.

命题3.2：由nm个独立部件所构成的并-串联系统L中，若每个串联子系统中部件个数都是n，且m个子系统中所有部件的寿命分布分别对应相同，即Fij(t)=Fj(t)，i=1,2,...,m，j=1,2,...,n，现验证此类系统在某种情况下可等价为一个串联系统.

解：由于系统L是阿基米德单调结构系统[1]，即系统L在t时刻累积失效率为：

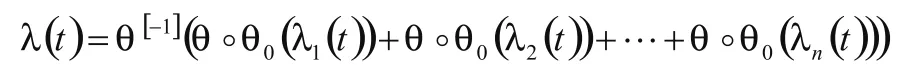
根据命题3.1的讨论结果，若m=2，且t∈[(n-1)1n2,+∞]时，φ[-1](t)=1-(1-e-t)2是n-单调的，故当t∈[(n-1)1n2,+∞]时，由2n个独立部件所构成的并-串联系统可等价为一并联系统。

说明：

1）在并-串联系统中，每个串联子系统部件个数都是n，且两个子系统中所有部件寿命分布分别对应相同，另外，n个部件之间是相互独立的.

2）等价后所成的串联系统中，每个部件的寿命分布函数和并-串联系统中部件的寿命分布函数存在关系并且串联系统中，n个部件寿命之间具有其中Cn是由所生成的n维Copula。

利用定理2.1还可以把部件之间不独立的一些复杂系统进行结构简化.

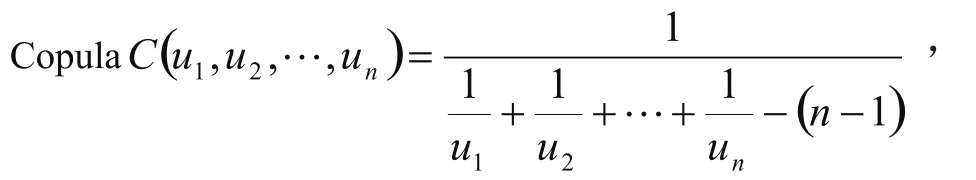
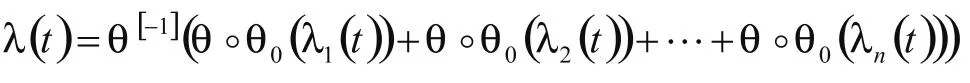
显然(θ(-1n(1-t)))[-1]不仅是n-单调，而且是完全单调的，故此系统可等价为一并联系统，如图所示：

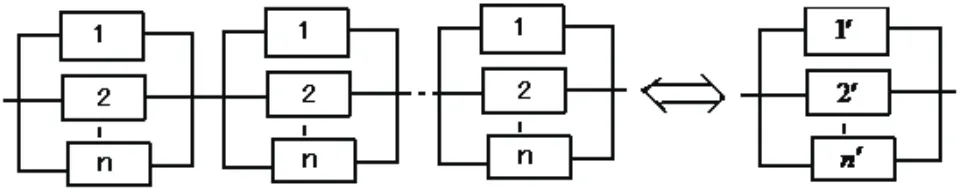
其中图中等价后所得的并联系统中，每个部件的寿命分布函数和并-串联系统中每个部件寿命分布函数存在关系i=1,2,...,n，且n个部件寿命之间具有Copula Cn，其中Cn是由所生成的 维Copula。

利用同样的方法可以把更多的阿基米德单调结构系统等价为结构较为简单的系统。通过系统的结构函数直接可以把系统简化，这一点充分体现了结构函数构造方法的优越性。

等价系统的寻找一直是一件比较困难的事情，文中提出的方法通过具体例子展示了其可行性，但是由于目前对阿基米德单调结构系统的研究刚刚开始，还没能够更多的寻找出属于这种特殊系统的系统类型，这一点在很大程度上限制了等价方法的应用.因此，寻找更多的属于这种系统的系统类型是今后的主要工作。

[1] 李霞,侯兵.系统结构函数的一种新的构造方法[J].华北水利水电学院学报,2009(3).

[2] 曹晋华,程侃.可靠性数学引论[M].北京：高等教育出版社,2006,143-144

[3] Sklar,A."Functions de repartition an dimensions et leurs marges",Publ.Inst.Statist.Univ.Paris 8,229-231,1959.

[4] Widder,D.V.The Laplace Transform(Princeton University Press,Princeton) [M].1941.

[5] Schweizer,B.and Sklar,A.Probabilistic Metric Spaces (North-Holland,New York)[M].1983.

[6] Feller,W.An Introduction to Probability Theory and Its Applications[M]Vol.Ⅱ,2nd Ed.(John Wiley and Sons,New York),1971.

[7] Roger B.Nelsen. An Introduction to Copulas [M].1998.