以学定教 找准位置——人教版六年级上册“位置”教学案例及反思

■关蓓

以学定教 找准位置
——人教版六年级上册“位置”教学案例及反思

■关蓓

以学定教是教学中恒久弥新的主题，直接指向学生的自主发展，而学生的自主发展既是教育的目标，也是衡量有效教学的标尺。以学定教，昭示着教师要改变过多地强调以教材和教参为中心的教学内容研究、以及教学设计以知识传递为主的价值取向，更多地关注学生现有状态（已有知识基础、个人经验）、个体差异、潜能、学习困难等，精心预设，促进生成。如何在教学中找准教与学的“位置”，已成为教育者对有效教学的必然诉求。

【课堂写真】

片断一：复习梳理巧开篇，找准知识固着点

1．复习用“第几”来描述物体在直线上的位置。

师：同学们，在一年级时我们就学过找位置，大家还记得吗？

（播放课件图1）：这是一排座位，你能说一说张亮的位置吗？用数几来表示？

生1：张亮的位置是从左数的第二个。

生2：张亮的位置是从右数的第五个。

图1

师：是啊，在这一排座位中描述张亮的位置，我们可以用数2来表示，也可以用数5来表示（课件演示图2），其他学生的位置也可以用一个数来表示。

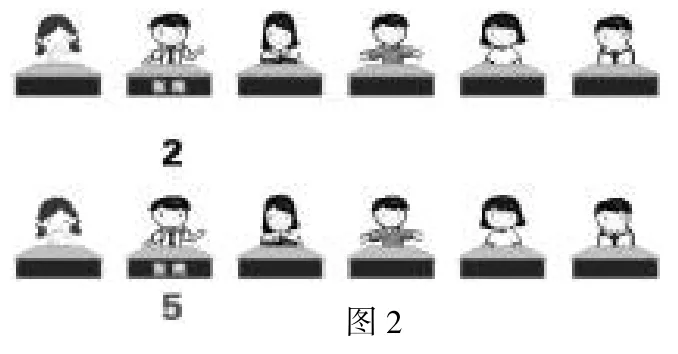
师：是不是这排座位中每个同学的位置都能这样来表示呢？

全班学生：是的。

师：看来在这一排座位中，不管是从哪边数，每个同学的位置都可以只用一个数来表示、来确定。

2．复习用“第几组第几个”来描述学生在教室的位置。

（播放课件：全班座位的情境图）

师：请看，教室里不止一排座位，同学们都坐得整整齐齐的，现在你还能说一说张亮的位置吗？

生1：张亮的位置在第三横排从左数的第二个。

生2：张亮的位置是第二列第三行。

生3：张亮的位置是第三排的第二个；

生4：张亮的位置在第二竖行最中间的一个。

生5：张亮的位置是倒数第三排的左数第二个。

师：看来张亮同学在教室里的位置，不能只用一个数来表示、来确定。

片断二：众说纷纭找位置，自主探究识数对

1．自主尝试，记录位置

师：大家都描述了张亮的位置，虽然方法不同，但有一点是共同的：都是用了两个数据来确定位置，一个是行数，一个是列数。能试着采用简洁的方法记录张亮的位置吗？请先想一想，再在纸上写下来。

（学生记录下张亮的位置后，有的学生用文字记录，有的学生用数字或符号记录，如2/3，3/5←，→2个3）

师：请解释你记录的含义。

生1：我写的是第二列第三行。

师：这是xx同学写的，你能解释是什么意思吗？

生2：第二列第三行。

师：你还写了一个符号，为什么呢？

生2：这样可以明确地表示他的位置。

师：这个同学（指生3）和这个同学（指生4）有箭头，你们明白吗？请这位同学（生3）来解释一下吧。

生3：箭头表示这个同学的位置在从左往右数的第二列，从前往后数的第三行。

生4：我这是从前往后数的第三行，从右往左数的第五列。

师：听了你们的解释，我们明白了。

2．约定统一，认识数对

师：刚才记录时有的同学用的文字，有的用的数字，有的同学添加了箭头符号，标明了数的方向……各有特点，都不错！这些写法有一点是相同的，就是它们都用了几个数？

生齐：两个数。

师生：一个是——行数，一个是——列数。

师：大家记录得很好！但是各人是各人的方法，如果别人看不懂，还得去解释。怎样记录能让所有的人一目了然，一看就能知道张亮的位置呢？你们有没有什么好的建议呢？

生：把它们规范一下。

师：好，我们就作约定，先写列数，后写行数。（板书：列,行）

师：你们说，张亮的位置在第几列？

……

师：用2、3就能表示张亮的位置，中间还要用一个逗号，你们知道为什么吗？

生1：如果没有隔开，就会把它看成23列了。

师：逗号就是起一个分隔的作用，2和3共同来表示张亮的位置，我们给它添上一个括号。（教师给2、3添加括号）像这样的两个数就是一对数，这样的形式有一个名字叫数对。用（2，3）这个数对就可以表示张亮在教室里的位置。大家看，数对中的形式多简洁啊，一看就明白了！

3．观察思考，提炼方法。

（演示课件）小精灵明明提问：同学们，你能用数对表示王艳和赵强的位置吗？看看有什么不同？

师：谁来说说王艳和赵强的位置？

生：王艳和赵强的位置分别是（3，4）、（4，3）。

板书：（3，4）（4，3）

师：请大家看一看，这两个数对有什么不同？同位之间互相说一说。

师：说说你们的发现。

生1：王艳的（3，4）是指第三列第四行。而赵强的（4，3）是指的第四列第三行。这两个数对表示的含义不同。

师：所以他们的位置也就不同。还有谁补充？

生2：它们的数字是一样的，但顺序不一样。王艳是3在前，4在后。赵强4在前，3在后。

师：顺序不一样，所以表示的位置也不一样。

师：要把数对写正确，你们有什么要提醒大家的？

生3：数对不要写反了，第一个数表示列，第二个数表示行。如果写反了，表示的位置就不一样了。

师：是啊！写数对的时候，一定要先写列数，再写行数。这位同学的小提示很重要，我们用掌声来感谢一下！

师：小精灵聪聪还有个问题。（课件出示：“确定一个学生的位置，用了几个数据？”）谁来说一说？

生1：确定一个学生的位置，用了两个数据。

生2：只用一个数据。

师：是吗？你说说这个数表示什么？

生2：呵呵，我说错了，应该是两个数，一个是列数、一个是行数。

师：明白了就好！数对可以帮助我们简明扼要地描述某个地点的位置。是谁这么聪明，最先想出数对的呢？想知道吗？

生：想。

师：他就是法国数学家笛卡尔。

片断三：联系生活用数学，学以致用找位置

师：数对的发明解决了人们确定位置的问题，生活中还有很多确定位置的例子，你们知道吗？并说说确定位置的方法。

生1：电影院里找座位。

师：在电影院里看电影需要找位置（演示课件：电影院座位）。老师这里正好有一张电影票，是1号厅2排13座，有谁能帮我找到这个位置？说说你是怎么找的。

生2：乘坐飞机时要凭登机牌。

师：请看（课件出示）登机牌上座位写的是9A，你怎么去找到这个位置呢？

……

师：你们知道经度和纬度的知识吗？我们一起来了解一下。

（课件演示：介绍经纬度）经度和纬度也是两个数据，可以帮助我们确定地球上某一点的位置。例如，我们在谷歌地球的软件中输入育才小学的经度和纬度，就能搜索到我们上课的第二阶梯教室所在的位置了。

生：太神奇了！

【课后反思】

“以学定教，找准位置”就是要以现代教学设计的核心思想——“教以学为基础（加涅）”为指导，从学生的学习状态和发展需要出发，进行开放且有弹性的预设，为师生的共同发展提供前提保证，促进课堂教学的动态生成——“课堂教学就是师生共同生成意义、交流意义的场所”（钟启泉）。在这一过程中，往往容易把握教师的“教”，而如何找准学生“学”的位置却被忽略。在这个案例中，着重从以下几个方面作了尝试：

一、找准学生学习的起点，夯实基础

学生要建构属于自己的知识，必须要有一个清晰和有力的固着点，这个“固着点”往往蕴含着丰富的内涵，具有迁移力、再生力强这样的特点，能同化或顺应新的知识，以利于学生自主地展开构建过程。在这个案例中，我设计了这样的环节：复习导入时找准学生的起点，用“说一说一排座位中张亮的位置”，梳理了“在一条直线上可以用一个数来描述物体或点的位置”，这是学生已有经验；再“说一说教室里张亮的位置”，提出了“看来张亮的位置不能只用一个数来表示、来确定”的想法，不仅激发了学生思考“到底要用几个数来表示呢”？而且为学生探究在平面内确定物体的位置提供了知识生长的“固着点”。在这个基础上，引导学生从教室里座位图的具体情境所提供的感性材料中抽取、概括数学概念——什么是“数对”，进一步激活学生的已有经验，架起数与形之间的桥梁，从而建构确定某一物体在“线、面”上位置的知识系统：在直线上的点只用一个数确定位置，在平面上的点只用两个数即可确定位置，并为今后学习埋下伏笔，即在三维空间中的点用几个数可确定位置？进一步加深了学生对“数对”的理解，使学生领略到数形结合思想及转化方法的精妙——“数缺形时少直观，形缺数时难入微”。

在案例中，教师还十分注重在“用数学”中进一步夯实基础。通过提供在电影院、飞机上找座位的例子，说说确定位置的方法，既让学生深切感受到数学与生活的密切联系，数对在生活中的运用，又学会用数学的眼光看待问题——用数对来确定位置或者用数对来描述位置等；还特别介绍了经度、纬度的小知识和谷歌地球搜索软件，使学生明确运用经度和纬度这一对数就能确定地球上任意一点的位置，提升了学生的数学素养，发展了学生的空间观念。结合教学内容，巧妙地激发了学生的兴趣：“数对可以帮助我们简明扼要地描述某个地点的位置。是谁这么聪明，最先想出数对的呢？”此时，恰到好处地介绍法国数学家笛卡尔和他建立的平面直角坐标系的小知识，让学生体会到平面直角坐标系的建立，架起了一座几何问题与代数问题之间相互转化的桥梁。学生通过本单元的学习，又站在了新的起点上，为第三学段，即七年级下学期学习《平面直角坐标系》的内容夯实了基础。

二、解决学生学习中的困难，体现“数学化”

弗赖登塔尔曾指出：与其说是学习数学，还不如说学习“数学化”。何谓“数学化”？即从实际问题中抽象出数学知识以及在较低层次数学基础上，抽象出更高一级的数学知识。对于学生而言，认识“数对”这个概念并没有什么难度，关键是要理解为什么“教室里要用两个数据确定学生的位置”和两个数顺序的重要性，并纳入到已有的知识结构中，形成新认知结构，解决实际问题。由于用“数对”描述平面内点的位置，实际上是将几何问题用代数方法来解决，不少学生理解上有困难，是学生数学思维的一次飞跃，所以以往关于“数对”的教学是安排在中学阶段的。在新一轮课程改革实验中，新课标教材安排在小学六年级上册的第一单元《位置》中教学，是考虑到学生在生活中已经初步具备了一些确定物体位置的经验，并通过前几个年级的学习获得了确定物体位置方面的相关知识。一年级下册在《位置》这一单元中，经历过用“第几组第几个”、“第几行第几个”等表述人或物体的位置。四年级下册在《位置与方向》这一单元中，获得了在平面内可以通过两个条件确定物体位置的初步经验和知识。在这个基础上，本节课的学习还是可行的。为此，在本课教学中，教师充分考虑到学生认知的困难，紧扣“如何用数描述形？如何用形反映数？”这一教学重点和难点，依据学生的已有知识经验，通过情境链（一行学生到多行学生）、引出问题串（怎样表示张亮的位置？怎样表示简明、准确），在引导学生从数的角度描述点在平面上的位置的同时，渗透数形结合、符号化的思想，让学生学会在平面上用数对表示点的位置的方法，进而学习如何在方格图上用数对确定物体的位置。这是一个“数学化”的过程，学生经历了一系列具有挑战性的探索、体验活动，先从多次由于“不统一”带来的矛盾冲突中自主寻求“破解之道”，提出约定达成共识：如“横行竖列”、“先写列后写行”、“从左往右确定列”、“从前往后确定行”等等，再从具体情境中抽象出“数对”的概念，理解数对的含义和确定位置的方法，也对小学阶段“空间与图形”领域中有关“位置”的内容进行了整理归纳，形成知识网络系统。

又如在联系生活用数学的教学中，飞机登机牌上出现了“9A”这样的形式，这是“数对”吗？很多学生心中会有疑惑，这无疑又是一个“数学化”的过程。教师在教学时没有一带而过，而是利用了这个学习资源。因为9是一个数，字母“A”可以代表数，那么“9A”就可以看作是一对数来确定座位——第九排第A座。至于为什么飞机登机牌上确定位置的数对是“先行后列”、“数9与字母A之间为什么不用逗号隔开”等等问题，则可以放手让学生互相讨论，相互答疑，培养学生的数学思考力。

【问题讨论】

正如杜威所说：“真正思考的人，从自己的错误答案中吸取的知识比从自己成就中吸取的只是更多，错误与探索相联姻，相结合，才能孕育出真理。”在这节课的教学中，也有这样的问题要进一步思考：在要求学生记录张亮的位置时，大部分学生记录的方法比较单一，以文字记录居多，这反映了学生思维方式的狭隘和符号化意识的单薄，举一反三的能力弱化。对于即将步入中学学习的学生而言，无疑会导致出现中小学生学习方法衔接上的问题，应该引起重视并在教学中补缺。如何实施，则有待实践去探求了。

（作者单位：武汉市育才小学）

责任编辑 廖林