基于频差控制的自适应频率检测研究

徐艳春,瞿晓东

(黑龙江大学 机电工程学院,哈尔滨 150080)

0 引 言

微弱信号检测技术大量应用在光、电、磁、声、热、生物、力学、地质、环保、医学、激光、材料等领域[1]。微弱光电信号频率检测的研究是目前微弱信号领域的一个新热点,由于待检目标绝对值小、信号弱,同时,在实际测量时又受到温度噪声、热噪声、复合噪声以及背景噪声等影响,表现出的总体效果是有用信号被大量的噪声和干扰所淹没,而目前常规测量装置很难对如此微弱的光电信号进行精确可靠的检测。因此,研究微弱光电信号检测算法,研制新的微弱信号检测装置是如今检测技术的一个重要方向[2]。

随着混沌理论的发展以及混沌理论在信号检测领域的应用,国内外学者提出了许多在强噪声背景下检测微弱周期信号幅值和频率的方法,其中绝大多数方法都是假设待检信号的频率已知[3-4],从而去检测未知信号的幅值,然而,当待检信号的频率未知时,很多检测方法失效。

研究表明,利用低阶的Duffing混沌系统检测微弱光电信号频率时,系统以Δw为频率出现间歇混沌。当Δ w≤0.03时,有规律的间歇混沌状态能够被辨别出,而当Δw＞0.03时,Duffing混沌系统检测微弱光电信号频率方法误差较大,因此为了能够灵活精确地检测微弱光电信号的频率,本文提出基于频差控制的自适应频率检测方法,从而加快微弱光电信号频率检测的速度,提高检测精度和稳定性[5-6]。

1 Duffing混沌振子检测微弱光电信号原理

Duffing方程是描述一个非线性弹性系统的运动方程,是1918年Duffing通过对具有非线性恢复力项的受迫振动系统的深入研究后提出的标准动力学方程,经规范化后又由Holmes等人进行了深入的研究,故也称为Holmes型Duffing方程,因为方程阶数低,结构简单,而被广泛应用到微弱信号检测中[7]。

设待检信号为:

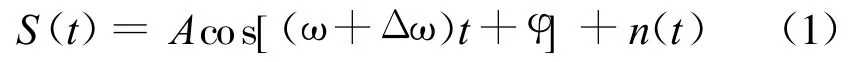
式中A为有用周期信号的幅值;Δω为绝对频差; φ为待检测信号与周期策动力的相位差;n(t)为噪声信号。

将待检测信号加入到Duffing方程中,则Duffing方程为:

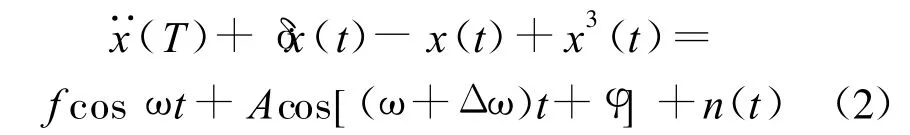
式中 f为周期策动力的幅值。

式(2)也可化为:

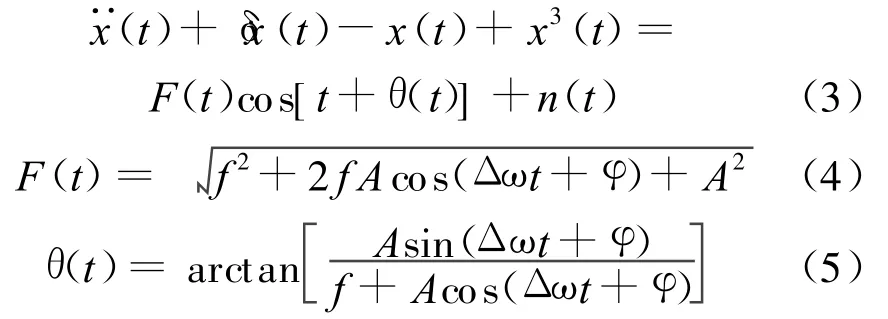
式中F(t)为总策动力幅值;θ(t)为总策动力的初相角。

分析式(4),f-A≤F(t)≤f+A,根据Duffing方程检测微弱信号的原理,将f设定在fd附近,在总摄动力的作用下,系统以Δω为频率出现间歇混沌。大量的实验表明,当Δω≤0.03时,有规律的间歇混沌状态能够被辨别出。采用78个固有频率以公比1.03成等比数列的振子构成阵列, ω1=1 rad/s,ω2=1.03 rad/s,ω3=1.060 9rad/s,…,ωk=1.03ωk-1rad/s,…,ω78=9.738 rad/s。

若频率在1～10 rad/s的被检信号输入到阵列中,就会在两个相邻的振子上发生稳定的间歇混沌运动,由此检测出信号的频率。得出如下结论:

1)当Δω=0时,待检信号频率和周期策动力的频率相同,通过策动力的频率即可知待检信号的频率。

2)当Δω≠0时,存在微小的频差,系统将时而进入周期状态,时而进入混沌状态,出现间歇的混沌状态。

当待检信号通过振子阵列时,发生间歇性混沌现象的两个相邻的阵子频率范围为 1～10 rad/s,分别为则此时待检测信号频率ω的被检测到的范围为:

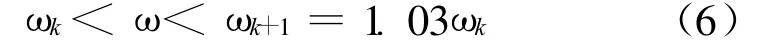
根据上述特性,假设待检测周期信号的频率为1～10 rad/s,可以检测未知信号的频率。若被检测周期信号频率不在此范围,必须提前对信号的频率进行处理,通常以速度V来对信号进行记录,然后以10n(n=…,-2,-1,0,1,2,3,…)的速度重放出来,重放信号与n在频率1～10 rad/ s之间一一对应,确定重放信号的频率后再乘以10-n,就可得到原信号的频率。

振子阵列法的检测流程见图1。

具体计算方法如下:

假设n=-3,第20号振子(ω20=1.753 5 rad/s)和第21号振子 (ω21=1.806 1 rad/s)都发生了稳定的间歇混沌现象,间歇混沌的周期 TΔ1、TΔ2分别为376 s和178 s,因此,得到频差Δω1= 2π/TΔ1=0.016 7 rad/s,Δω2=2π/TΔ2=0.035 3 rad/s,最后计算出信号的频率为:

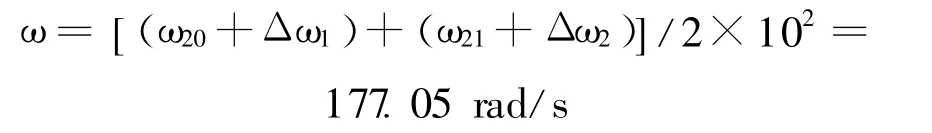
增加混沌振子数,可以检测其它频率范围。

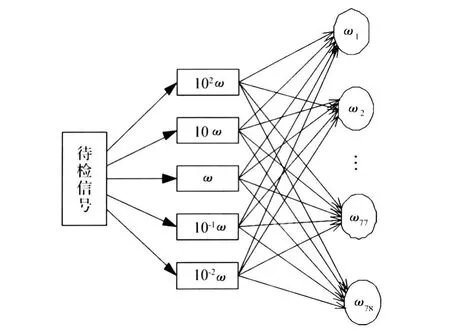
图1 振子阵列法的检测流程图Fig.1 Flowchart of the oscillator array method

该方法由于混沌振子阶数较低,方程简单,研究和使用方便,从而得到了很多学者的青睐,但是,该方法需要使用78个混沌振子,数目较多,从而其具有较大的局限性[8-10]。

2 基于Rössler混沌控制的微弱光电信号频率检测原理

Rössler系统方程为:

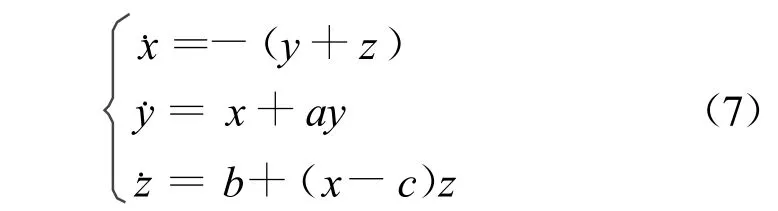
式中a,b,c为系统参数。

Rössler系统是一个三阶自治系统,含有一个非线性项xz,正是这个非线性项使系统产生分叉、混沌等复杂的动力学行为[11]。其中方程在a=b= 0.2,c为不同值时,Rössler吸引子的形状见图2。

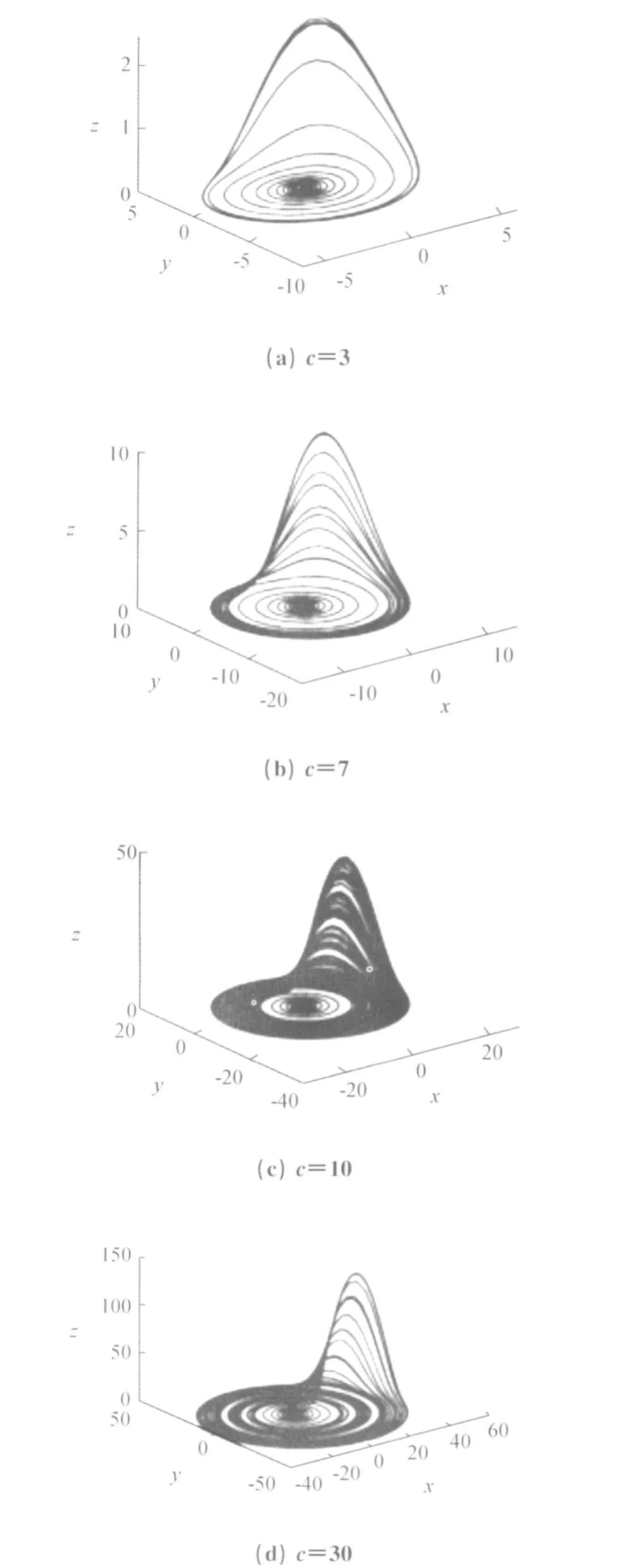
图2 c为不同值时Rössler吸引子相图Fig.2 Phase diagram of Rössler attractor when parameter changed

从理论上来说,将待检测的微弱信号加入到3个方程中的任一个方程均可改变系统的动力学行为,当系统处于混沌的临界状态时,加入待检测的微弱信号,系统从临界状态跃变到混沌状态,此时,采用比例微分控制策略[12],将系统控制到稳定周期态后,再用频谱分析方法则可测出未知信号的频率。

具体控制算法及步骤如下:

1)调整Rössler混沌系统参数c,使其处于混沌的临界状态;

2)加入含有噪声的待检测的微弱信号,从而系统进入混沌态;

3)采用上述比例微分控制策略,调整控制参数,使其从混沌态进入周期态;

4)控制后的系统输出中含有待检信号的信息,对其进行频谱分析,从而检测出待检信号的频率。

该方法通过比例微分控制,实现了对微弱光电信号的频率检测,但由于Rössler混沌方程阶数较高,控制过程相对复杂,尤其将混沌的动态特性从混沌态控制到大尺度周期状态时,控制难度大,检测速度慢,因此也有一定的局限性。

3 基于频差控制的自适应频率检测

根据Duffing混沌系统检测微弱光电信号频率的原理,系统以Δω为频率出现间歇混沌。研究表明,当Δω≤0.03时,有规律的间歇混沌状态能够被辨别出;当Δω＞0.03时,Duffing混沌系统检测微弱光电信号频率方法误差大,因此可以采用基于比例微分控制策略的Rössler混沌振子检测微弱光电信号频率方法,然而,由于Rössler混沌振子为高阶的混沌振子,其混沌动态特性复杂,阶数较高,对其有效的实现比例微分控制,控制过程复杂,而Duffing混沌系统结构简单,阶数较低,计算方便。两者相比,彼此具有各自的优缺点,因此,为了灵活方便的检测微弱光电信号频率,本文提出基于频差控制的混沌振子自适应选择策略,其原理框图见图3。

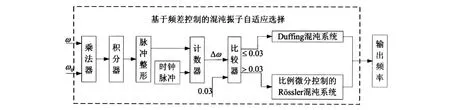
图3 基于频差控制的自适应频率检测原理框图Fig.3 Principle diagram of chaos adaptive selection based on frequency deviation control

图3中,ω0=2πf0为Duffing混沌系统周期策动力的已知频率,ω=2πf为待测微弱光电信号的未知频率,将两个不同频率的正弦输入信号送入乘法器,互相调制后输出信号呈周期性变化,变化的频率正好就是频率差Δω,将Δω与0.03相比,若Δω≤0.03,则选用方程结构简单的Duffing振子阵列法检测微弱光电信号的频率;若Δω＞0.03,则采用本文提出的比例微分控制的Rössler混沌系统实现微弱光电信号频率的检测,使检测手段更加灵活方便。

图4给出了一个频率差的实验波形图,其中,图4(a)、图4(b)表示的是两个不同频率的正弦输入信号,将它们送入乘法器,就可以得到图4 (c)所示的波形,由图中可见,互相调制后输出信号呈周期性变化,变化的频率正好就是频率差Δf。因此,通过积分器对高频的抑制就可以将低频分量提取出来(图4(d)),再经计数器就可以得到精确的频率差Δf,并可以作为测量数据直接输出。

应用上述基于频差控制的自适应频率检测方法对不同输入信噪比情况下的微弱光电信号频率检测进行仿真分析,并将其与比例微分控制的Rössler混沌系统检测方法和Duffing振子阵列法检测结果进行比较,检测结果见表1。

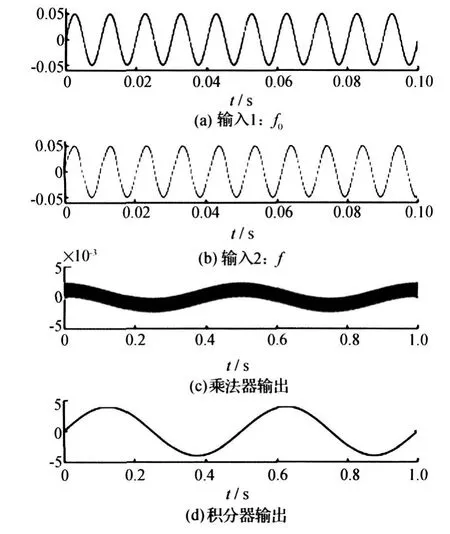
图4 频差测量的实验波形图Fig.4 Experiment waveform diagram of frequency deviation measurement

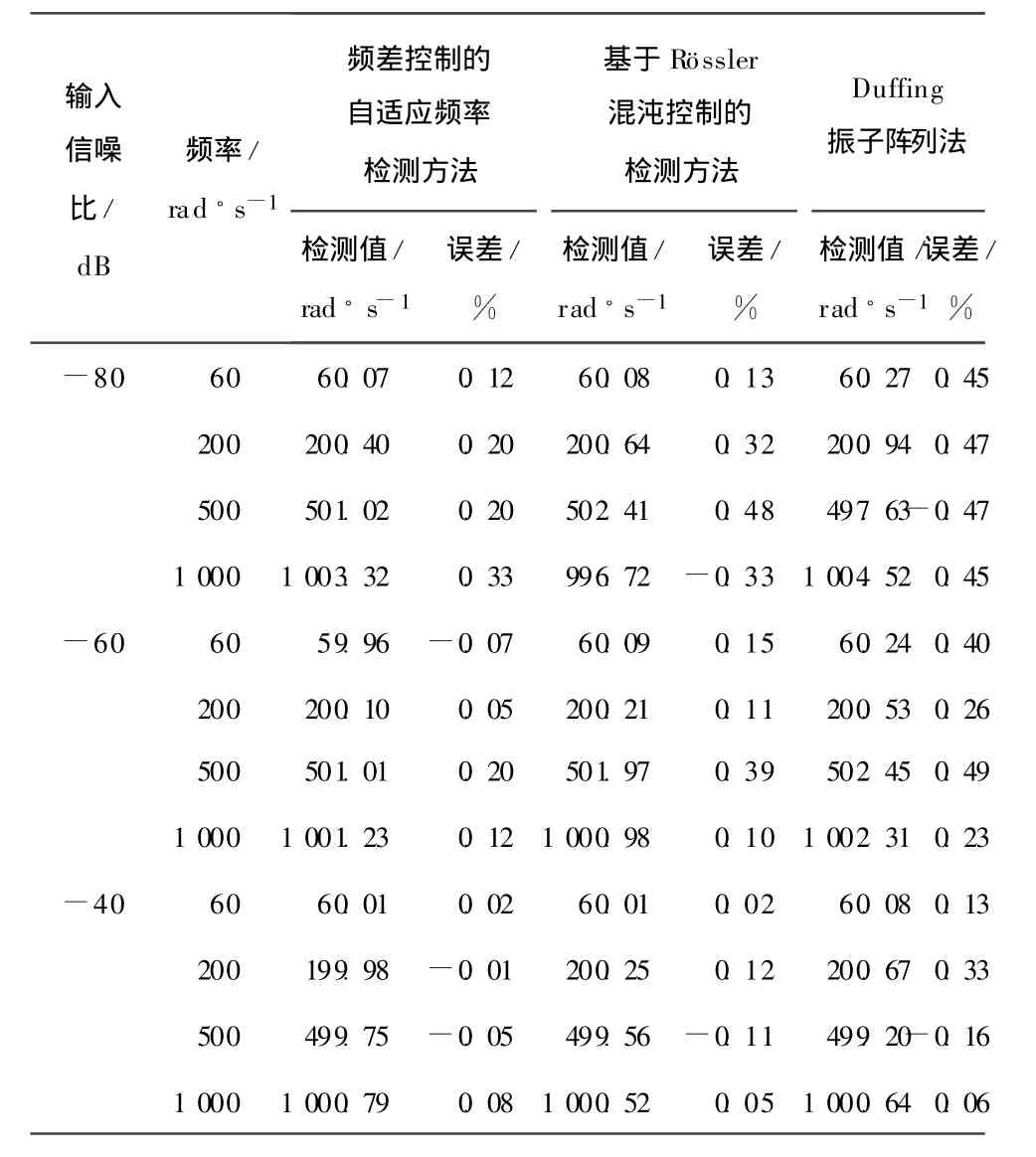
表1 基于混沌模型的自适应频率检测结果及比较Table 1 Adaptive frequency detection result and contrast based on chaos model

由表1可见,利用本文提出的基于频差控制的混沌振子自适应选择检测微弱光电信号频率是可行的,检测精度高,误差小,检测手段方便灵活。

为了验证基于频差控制的自适应频率检测方法的稳定性,进行了大量的仿真分析,设输入信噪比为-60 dB情况下,待检信号频率为100 rad/s,仿真结果见表2。

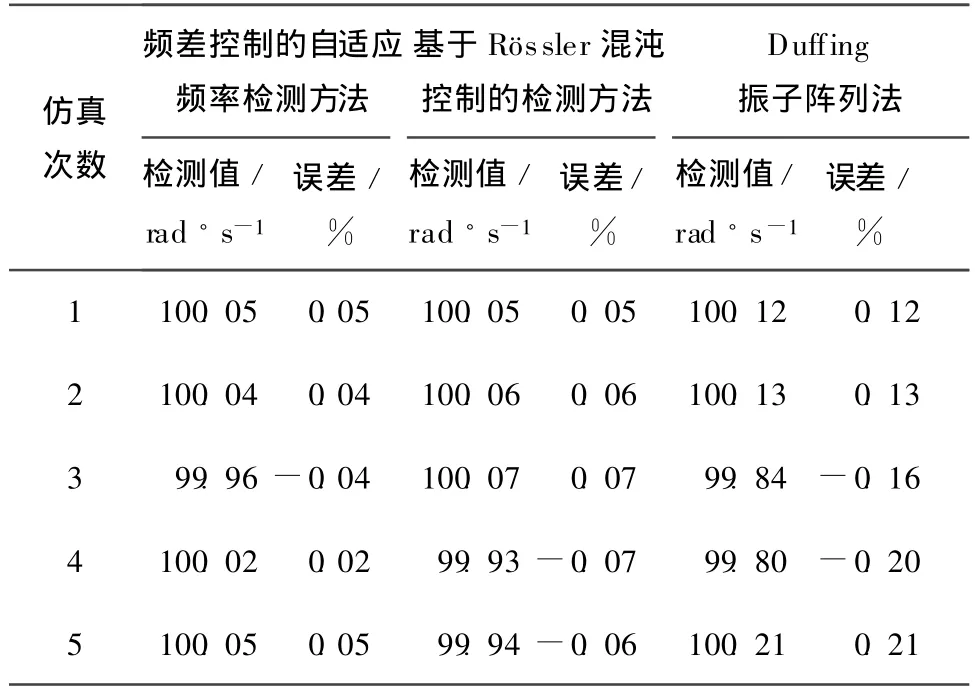
表2 频率检测方法稳定性分析Table 2 Stability analysis of frequency detection methods

由表2可见,采用频差控制的自适应频率检测方法稳定性较好,检测精度高,误差小。

4 检测实验与误差分析

实际检测中微弱光电信号通常被强噪声所淹没,为了模拟实际系统中的噪声,采用一台Agilent 81150A型函数信号发生器输出均值为零的白噪声。

实验中,F20函数信号发生器首先发出峰值为1 V,频率为1 kHz的模拟正弦信号,经衰减电路衰减为5.728 4×10-4V,另一台Agilent 81150A函数信号发生器发出噪声电平为0.5 V的白噪声,两者进行叠加,模拟被强噪声淹没的微弱光电信号并输入前置放大电路,从而进入系统进行检测,检测原理框图见图5。

基于混沌振子的微弱光电信号检测实验系统实物图见图6。

微弱光电信号的频率检测采用了本文提出的基于比例微分控制的Rössler混沌系统检测方法和基于频差控制的自适应频率检测方法,检测结果及相对误差记录于表3。

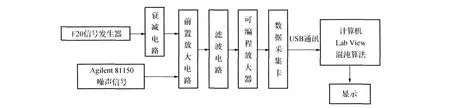
图5 实验系统原理框图Fig.5 Principle block diagram of experiment system

图6 基于混沌振子的微弱光电信号检测实验系统Fig.6 Experiment system of weak photoelectric signal based on chaotic oscillator

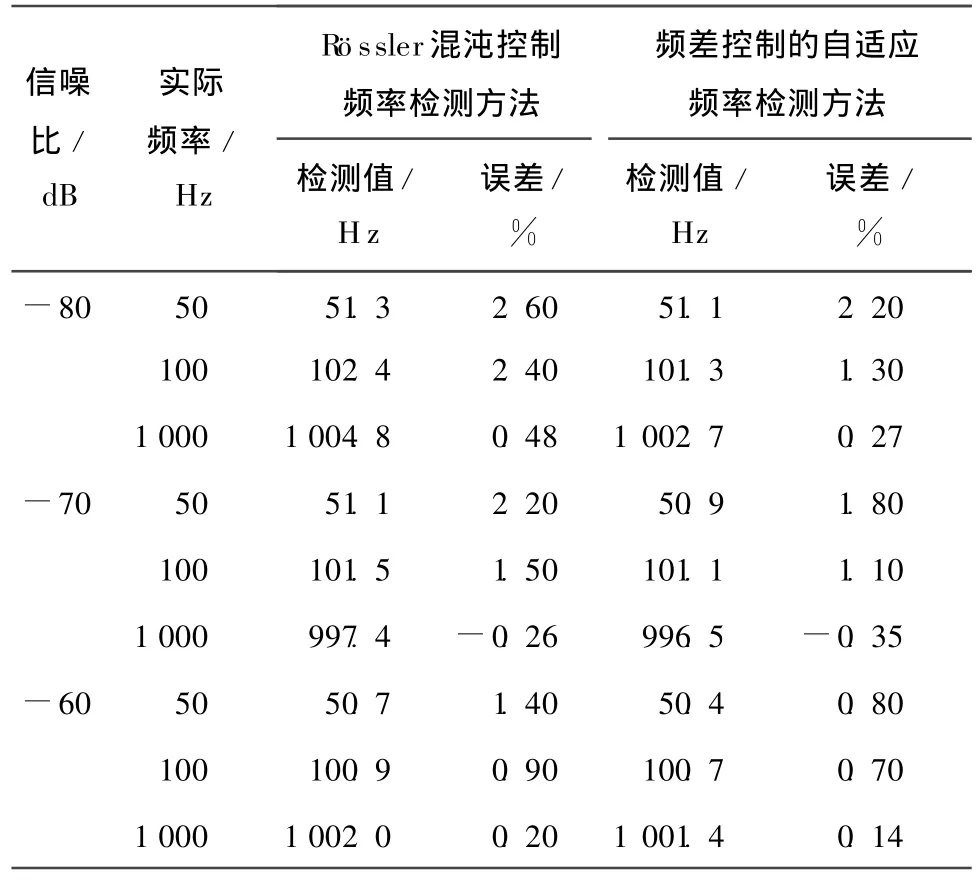
表3 信号频率检测结果及相对误差Table 3 Experiment result and relative error of the frequency

由表3可见,基于混沌振子的微弱光电信号检测系统检测信号频率也存在一定的误差,总之,影响检测精度的因素主要包括:

1)电气系统误差。电气部分的误差主要来源于电子器件的噪声、前置放大器的噪声和漂移、程控放大器的噪声和漂移以及数据采集系统的A/D量化误差等。经测试由探测器的噪声、前置放大器的噪声和漂移、程控放大器的噪声和漂移造成的误差＜0.1%,12 Bit的A/D量化误差为0.25%。由电气系统引入的误差合成后为:

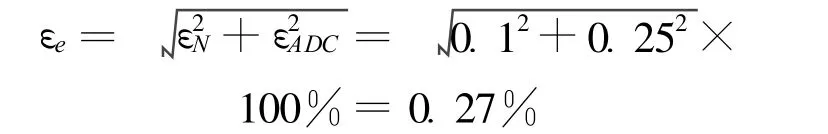
2)数据处理误差。在检测系统中,由于混沌系统临界阈值的确定以及系统状态初始值的调整和设定,系统都很敏感,尤其利用Lyapunov指数定量检测幅值过程中,阈值的计算也存在一定的计算误差,该误差εm＜0.75%。

3)数据采集误差。在数据采集系统中,通过USB通讯接口实现数据与上位机间的快速传输,在数据传输过程中,有时会出现数据丢包现象或者数据覆盖现象,从而导致数据采集的误差,该误差εd＜0.30%。

综合电气系统误差、数据处理误差和数据采集误差,基于混沌振子的微弱光电信号检测系统的测量误差可表示为:

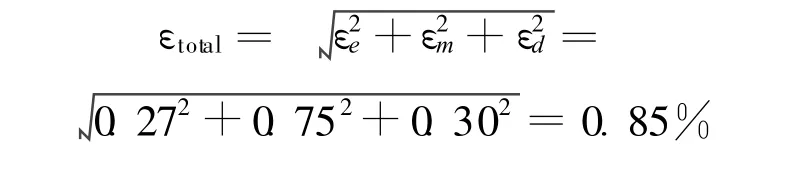
5 结 论

本文研究了Duffing混沌系统检测信号频率和基于比例微分控制的Rössler混沌系统检测微弱光电信号频率的方法,并通过对两种检测方法优缺点的分析,进而将两种混沌模型揉和在一起,提出基于频差控制的自适应频率检测方法,该方法通过对待检信号的频率与周期策动力频率之间频差的控制,实现两种混沌振子之间的自适应选择,从而加快了检测速度,检测精度高,误差小。同时,也对基于频差控制的自适应频率检测方法进行了稳定性分析,仿真结果证明该检测方法稳定性较好。

[1]G.Y.Wang,S.He.A Quantitative Study on Detection and Estimation of Weak Signals by Using Chaotic Duffing Oscillators[J].IEEE Transactions on Circuits and Systems-Fundamental Theory and Applications, 2003,50(7):945-953.

[2]Y.G.Yua,H.X.Li.The Synchronization of Fractional-order R ö ssler Hyperchaotic Systems[J].Physica A.2008,387:1393-1403.

[3]聂春燕.混沌系统在弱信号检测中的应用[J].传感器技术.2003,22(1):55-57.

[4]C.Y.Nie,Y.W.Shi,Z.W.Wang,et al.A Detection Method of Signal Frequency Based on Optimization Theory[C]//Proceedings of SPIE-the International Society for Optical Engineering,Beijing,China.2006: 345-348.

[5]Y.Li,B.J.Yang.Physical Mechanism of the Chaotic Detection of the Unknown Frequency of Weak Harmonic Signal and Effects of Damping Ratio on the Detection Results[J].Chinese Physics.2006,13(9):1 386-1 390.

[6]尚秋峰,尹成群,李士林.基于Duffing振子的微弱正弦信号检测方法研究[J].中国电机工程学报,2005, 25(2):66-70.

[7]张 鑫,陈伟斌,姚明海.Duffing振子检测微弱正弦信号的普遍性研究[J].计算机与数字工程,2005,12 (33):71-73.

[8]李 月,杨宝俊,石要武,等.混沌振子用于强噪声下微弱正弦信号的检测 [J].吉林大学自然科学学报, 2001,1(1):75-77.

[9]Deng Chang-jian,Zhang Shao-quan.The Weak Signal Detecction Based on Chaos and Genetic Algorithms [C]//Information Science and Engineering(ISISE), 2009 Second International Symposium.2009,579-582.

[10]L.Nana,T.C.Kofane.Chastic Behavior in Deformable Models:the Asymmetric Doubly Periodic Oscillators[J].Chaos,Solitons&Fractals.2005,13(4): 731-740.

[11]陈士华,谢 进,陆君安.Rössler混沌系统的追踪控制与同步[J].物理学报,2002,51(4):749-752.

[12]王 伟,张秋富.R ö ssler系统的比例微分控制 [J].重庆工学院学报:自然科学版,2008,4(22):136-138.