切换线性随机系统的指数稳定分析:多Lyapunov函数方法

丛 屾,蒋海峰,盛遵冰

(1.黑龙江大学 机电工程学院,哈尔滨 150080;2.南京理工大学 自动化学院,南京 210094)

0 引 言

随着现代控制技术的发展,切换作为一种控制手段广泛存在于各种控制系统的数学模型中,从理论角度来说我们自然关心切换是如何影响系统动力学行为的。因此,在过去的十几年间切换系统成为控制理论领域中研究的热点问题,发展出来的方法与成果形成了一个独立研究分支。特别是与切换系统稳定问题相关的一系列研究成果丰富了动力系统理论体系并完善了Lyapunov稳定性方法[1]。

另一方面,在系统建模过程中引入噪声是反映各种振动现象及不确定因素的有效方式,因此我们将考虑具有状态时滞的切换随机系统并基于多Lyapunov泛函方法分析其在均方意义下的稳定性。较之于确定系统,随机系统包含更为丰富的研究内容,但是建立与之相应的理论体系却也更为困难,这是因为我们所使用的很多概念与方法潜在地依赖于具体的微积分法则。以切换系统为例,描述切换驱动的状态转移过程是准确分析系统动力学的基础[2-3];然而对于随机系统,除一维情形外,一般无法以闭合的形式刻划状态转移过程并以此分析其统计特性[4]。在随机分析的理论体系中考虑切换现象时通常假定其演化过程满足一定的统计规律,即所谓的时齐Markov过程。这一假设的理论意义在于,我们可以通过相应随机微分方程的无穷小生成算子间接反映切换驱动的状态演化的统计特性,而这对于分析其渐近性质是非常重要的[5-7]。因此,对于分别作为确定信号与随机信号的切换而言,比较文献 [7-8]与 [9-10]在建立基本概念与研究方法上都存在本质差别。

根据在样本空间上建立拓扑的意义不同,随机系统的稳定性含义也有所不同,常用的包括:依概率稳定,几乎必然稳定及均方稳定。在各种稳定性定义下,研究的重点在于如何利用噪声的统计特性及Itô微积分法则的不同侧面以分析状态随时间演化的统计规律。在依概率意义下,一般通过定义“状态离开原点某一领域”这一事件的发生时刻作为 “停时”,以此解析这一事件发生的分布律;然而建立确定意义下的 “切换”与随机意义下的 “停时”之间的因果关系并刻划其渐近性质是非常复杂的。在均方意义下噪声对稳定性的影响基本上是负面的[9],因此不利于分析噪声与切换对于稳定性的共同影响。在几乎必然意义下可以比较全面地认识噪声对稳定性的影响[8,10-11],但是多Lyapunov函数在切换时的不连续性致使我们无从建立其统计特性,即论证其是否呈上鞅;然而通过强大数定理可以描述状态演化的渐近性质,进而由此建立几乎必然指数稳定的条件。

1 问题描述

考虑如下切换线性随机系统:

其中x∈Rn为系统状态变量;ω(t)表示定义于完备概率空间上的一维标准化布朗运动,其参考族满足所谓的通常条件。

根据切换信号随时间的演化规律,可以将其展开为如下序列形式:

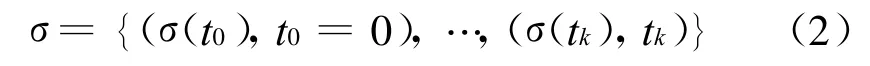
我们的目的是建立条件以通过抑制切换信号变化的剧烈程度来保证系统(1)是几乎必然指数稳定的。为此,对切换信号依据其变化剧烈程度进行分类。

定义2 给定Td＞0,切换信号σ(t)称为是属于STa的,如果其在任意区间 [t1,t2]内的切换次数称为是此类切换信号的平均驻留时间,是表征其变化剧烈程度的物理量。

用S∞表示在有限时间之后停止切换的切换信号所组成的集合,那么当Td1≥Td2时显然有STd1⊂STd2。

2 主要结论

由此结合Uxx=(1/V)Vxx-(1/V2)V′xVx即可推知:

及

那么,只要Td≥2ln χ/(β-2α),系统(1)在所有属于STd的切换信号驱动下都是几乎必然指数稳定的。

证明 构造子系统对应的Lyapunov函数如下:

根据式(4)及式(5)可以分别推知:

及

此外,必然存在γ＞0使得对于任意i=1,…,N有:

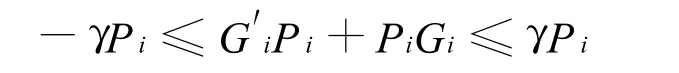
这意味着

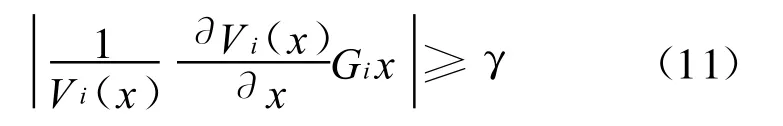
进而,由式(3)可知:

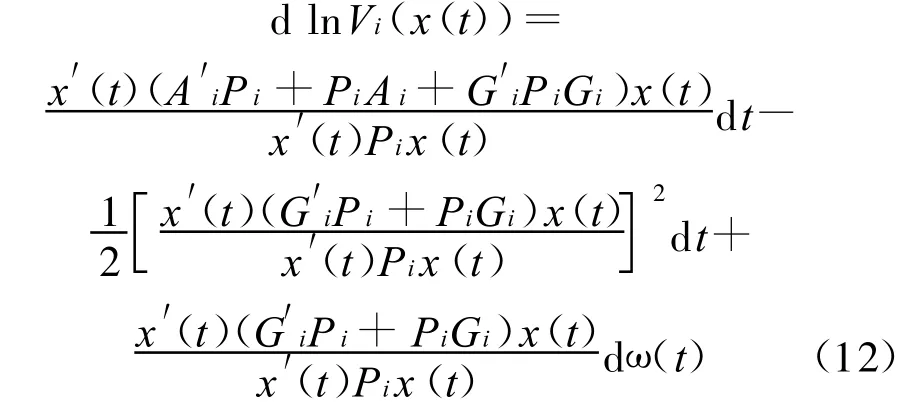
给定切换信号σ及任意时刻t,假设tk为t时刻之前的最后一次切换发生时刻,即在上再无切换发生,则有:

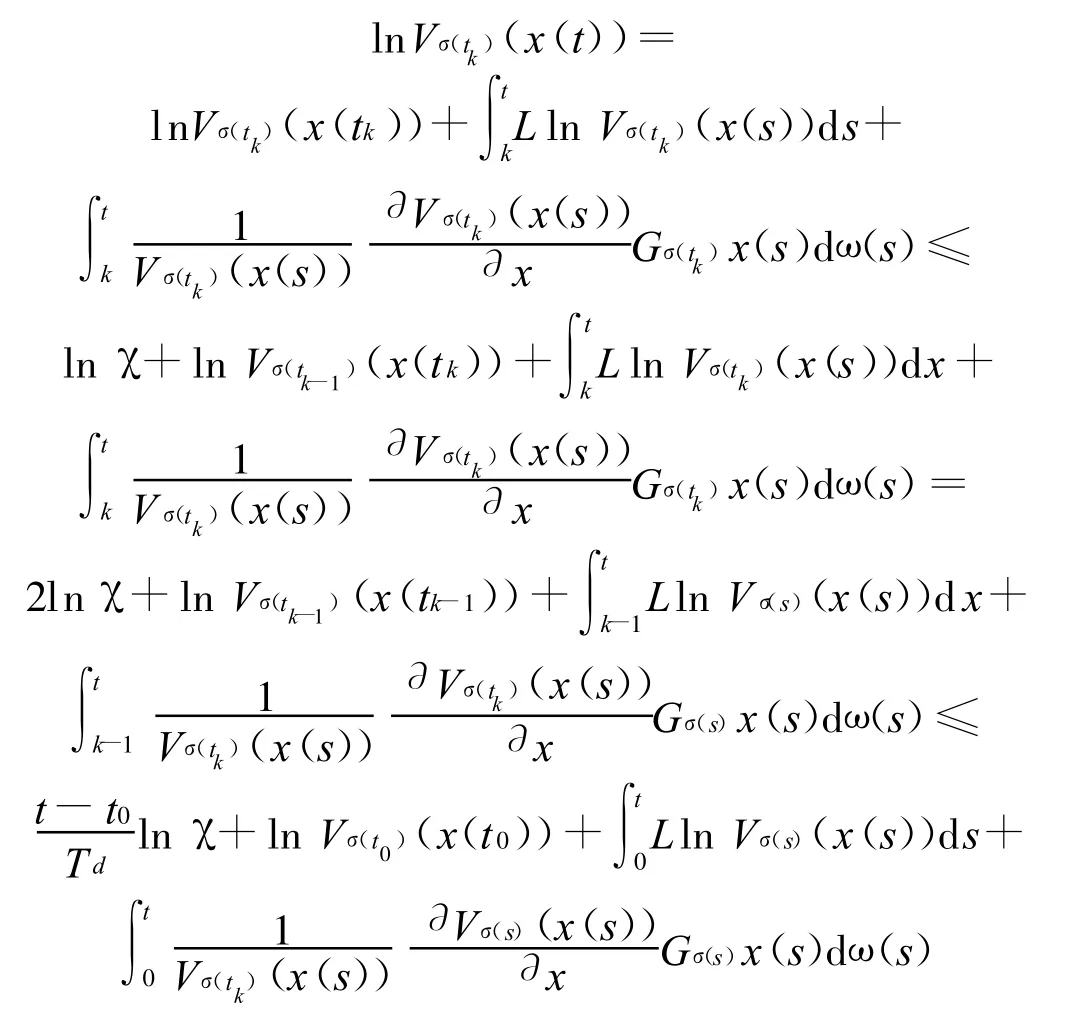
上述过程通过在切换时刻进行递归直至t0=0得到的,由此可以推知:

据此,根据强大数定理[9]推知:

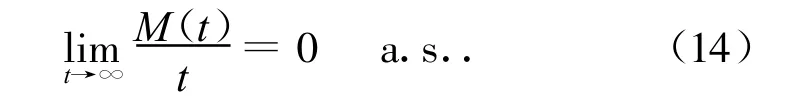
进而,将式(9)与式(10)代入式(13)即有:

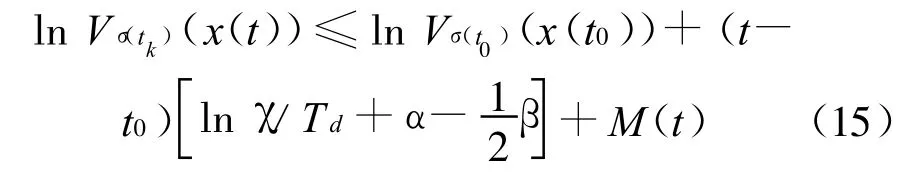
由此可见:

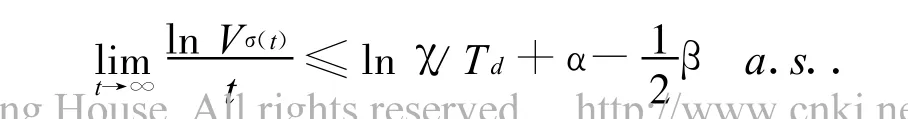
根据Td≥2ln χ/(β-2α)＞0便知:

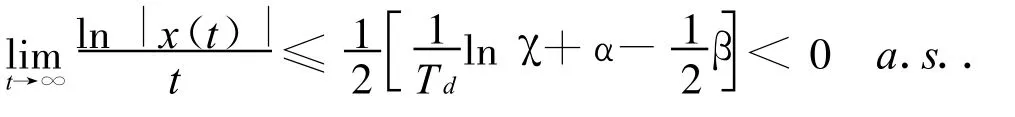
从而命题得证。

在稳定性分析的基础上,继续考虑控制系统的设计问题。为此,考虑具有控制输入u∈Rm的如下切换随机系统:

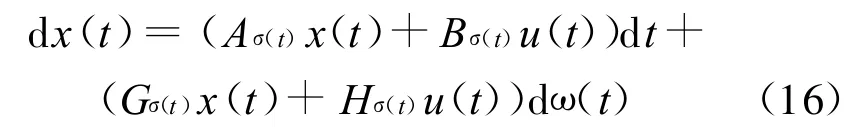
我们的目的是设计子系统反馈控制u=Fix;i =1,…,N:使得如下闭环系统

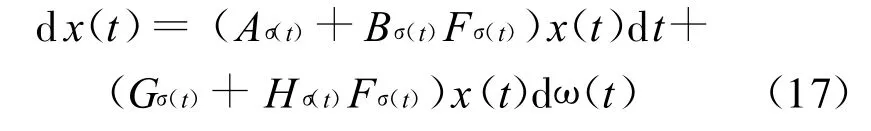
是几乎必然指数稳定的。通过简单的矩阵不等式技巧即可得证结论。

或者

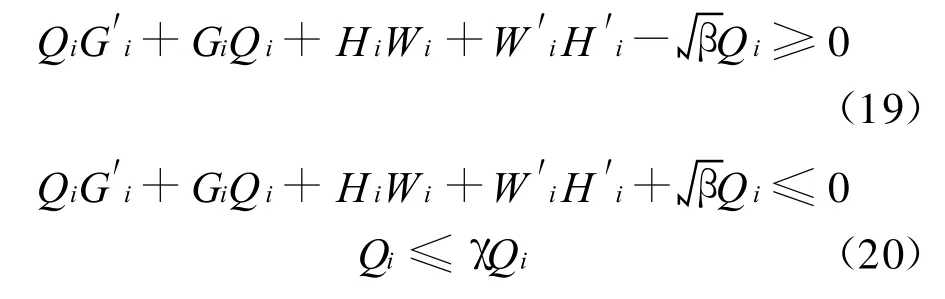
及

3 仿真算例

通过一个例子说明方法的有效性。

例1 考虑由两个二阶线性随机系统构成的切换系统,子系统方程如下:

及

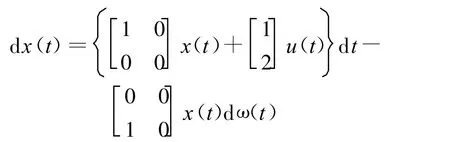
根据命题2,通过求解线性矩阵不等式得到子系统反馈控制分别为F1=[-0.766 1.732]及F2=[-0.055 -2.812],同时解得χ=2.07,α =0.34,β=3.0。据此,由上述子系统构成的切换是几乎必然指数稳定的,只要切换信号的平均驻留时间Td≥0.627。Brown运动及相应的状态响应分别示于图1与图2中。

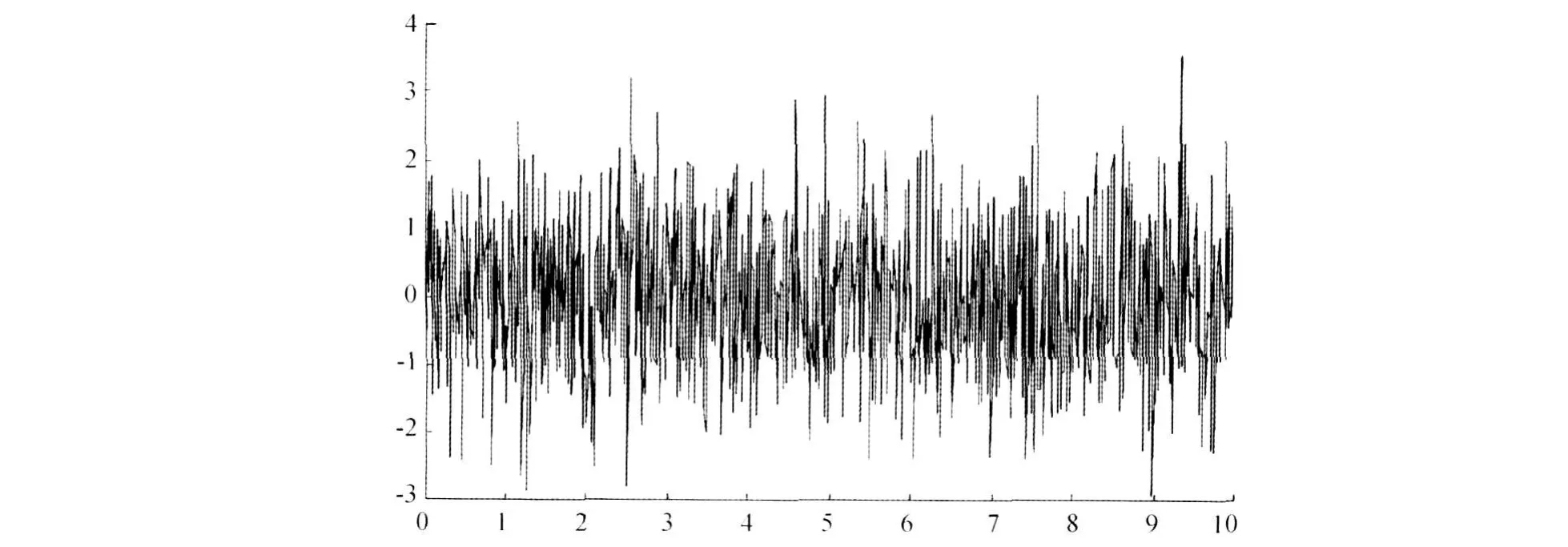
图1 一维标准化Brown运动Fig.1 1D normalized Brownina motion

图2 对应于Td=0.627系统状态响应Fig.2 State-trajectory corresponding to Td=0.627

4 结 语

本文考虑切换线性随机系统的稳定性问题,基于多Lyapunov函数方法结合强大数定理这类随机过程极限理论建立了这类系统的几乎必然指数稳定条件。进而,给出了子系统反馈控制设计条件,通过仿真算例验证了方法的有效性。

[1]D.Liberzon.Switching in Systems and Control[M]. Birkhäuser,Boston,2003.

[2]Geromel J C,Colaneri P.Stability and Stabilization of Continuous-time Switched Linear Systems[J].SIAM J.Control Optim.,2006,45(5):1 915-1 930.

[3]Sun Z,Ge S S,Lee T H.Controllability and Reachability Criteria for Switched Linear Systems[J].Automatica,2002,38(5):775-786.

[4] Mao X.Stochastic Differential Equations and Their Applications[M].Chichester:Horwood Publisher, 1997.

[5]Feng X,Loparo K A,Ji Y,et al.Stochastic Stability Properites of Jump Linear Systems[J].IEEE Trans. on Automatic Control,1992,37(1):38-53.

[6]Hu G,Liu M,Mao X,et al.Noise Suppresses Exponential Growth under Regime Switching[J].J.Mathematical Analysis Appl.,2009,355(2):783-795.

[7]X.Mao and C.Yuan.Stochastic Differential Equations with Markovian Switching[M].ImperialCollege Press,London,2006.

[8]Feng W,Tian J,Zhao P.Stability Analysis of Switched Stochastic Systems[J].Automatica,2011,47(1): 148-157.

[9]Wu L,Ho D W C,Li C W.Stabilization and Performance Synthesis for Switched Stochastic Systems[J]. IET Control Theory Appl.,2010,4(10):1 877-1 888.

[10]D.Chatterjee and D.Liberzon.Stability Analysis of Deterministic and Stochastic Switched Systems via a Comprison Principle and Multiple Lyapunov functions [J].SIAM J.Control Optim.,2006,45(1):174-206.

[11]F.Deng,Q.Luo,X.Mao,et al.Noise Suppresses and Expresses Exponential Growth[J].Systems& Control Letters,2008,57(3):262-270.