数控非球面超光滑加工机床空间误差建模

李显凌,柳艳杰

(1.中国科学院 长春光学精密机械与物理研究所应用光学国家重点实验室,长春 130033;2.黑龙江大学 建筑工程学院,哈尔滨150080)

0 引 言

随着计算机性能的提高和研抛工艺的发展,数控抛光已经成为超精密抛光技术的主流,包括磁流变抛光 (Magnetorheological finishing,M RF)[1]、离子束抛光 (Ion beam figuring,IBF)[2]和射流抛光 (Fluid jet polishing,FJP)[3]等抛光技术都采用了数控技术,其基本思想是根据光学表面面形检测的结果,由计算机控制加工参数和加工路径,完成加工。由于制造、装配、控制及运动过程中热变形、摩擦、振动和惯性等各种误差因素的影响,使得数控机床的实际运动轨迹难以同理想轨迹相吻合,造成加工误差,影响了被加工工件的加工精度,对数控机床进行误差补偿是提高加工精度的最为经济、有效的方法,而快速建立起准确的误差模型则是实施误差补偿的前提和基础,因此对数控机床进行误差建模研究具有重要意义。

多体系统理论[4]是解决复杂工程系统运动学问题和动力学问题的科学理论体系,具有很好的通用性和系统性。多体系统理论已在机器人、机床、坐标测量机等复杂机械的运动分析与控制中得到成功应用,并且应用领域正在不断扩大。以往的多体系统理论主要用于分析研究理想多体系统。近年来,多体系统理论开始用于分析研究有误差多体系统。

数控机床是一种典型的多体系统[5]。基于多体系统理论,以特有的低序体阵列来描述复杂系统,对数控机床进行误差分析和建模,不仅能全面考虑影响机床加工精度的各项因素以及相互耦合情况,而且能够充分利用现代计算机技术的发展成果,使建模过程具有程式化、规范化、约束条件少、易于解决复杂系统运动问题的优点,非常适宜于机械误差的计算机自动建模。

本文根据数控超光滑加工机床的拓扑结构,运用多体系统运动学理论的基本原理,使用低序体阵列来描述机床各部件的关联关系,使用齐次特征矩阵来表示各部件之间的几何特征,系统地推导出了有误差运动的数控超光滑加工机床运动学模型。建立了数控超光滑加工机床的空间误差模型,并给出了具体数学表达式。

1 拓扑结构和低序体阵列

数控超光滑加工机床的结构见图1,整个机床由回转工作台C轴和直线运动单元X轴,直线运动单元Z轴、回转运动单元B轴以及电主轴回转运动单元组成,用于球面和非球面光学元件的超光滑表面加工。

图1 数控超光滑加工机床结构Fig.1 Structure of the CNCsuper-smooth process machine

拓扑结构是对多体系统本质的高度提炼和概括,是研究多体系统的依据和基础。用低序体阵列方法描述多体系统拓扑结构简洁方便,是一种适用于计算机自动描述多体系统的方法,因此本文采用低序体阵列方法描述数控超光滑加工机床的拓扑结构。在多体系统分析中,把构成拓扑结构的单元称为体,描述体与体的关联关系的低序体阵列可通过下列定义的低序体运算得到。

多体系统中任意体j的n阶低序体定义[4]为:

式(1)～式(4)中,L称为低序体算子。

当L(j)=i时,称体i是体j的相邻低序体,体j是体i的相邻高序体。

图2为经过简化后数控超光滑加工机床的结构示意图,图中0为床身、1为工作台、2为工件、3为X轴导轨、4为Z轴导轨、5为摆动轴、6为电主轴、7为抛光头。对其进行提炼和概括,可以得到如图3所示的拓扑结构图。

根据上述低序体运算公式可以求出各体的各阶低序体号,从而构成表1所示的低序体阵列,它即是数控超光滑加工机床的低序体阵列。

表1 数控超光滑加工机床的低序体阵列Table 1 Low-order body arrays of the CNC super-smooth process machine

2 特征矩阵

在多轴数控机床中,各运动单元都有自己的运动轴名,如将工作台单元取名为w,刀具装夹单元取名t,除床身单元外,其它各体都有自己的名。为了使表达更简化、清晰和直观,可以将相邻体之间的运动及运动误差表达式的下标——相邻体标号“ij”+“s”改用其高序体的运动单元名表示,相邻体之间的位置及位置误差表达式的下标 “ij”+“p”改用除当其高序体为工作台单元或刀具装夹单元时用高序体的单元名+“d”表示外,用相邻体的单元名表示。这样,参考系也就不必命名。数控超光滑加工机床的特征矩阵见表2,其中,若特征矩阵等于 I4×4,则是因为考虑到误差相对很小(如运动部件的一些静止误差)或没有(如非运动部件的运动误差)。

3 综合空间误差模型

设刀具成形点在刀具坐标系内的坐标为:

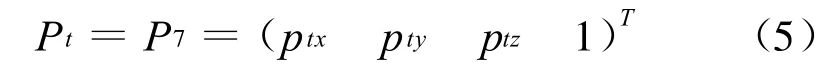
那么,刀具成形点在工件坐标系内的理想成形函数为:

设刀具路线为:

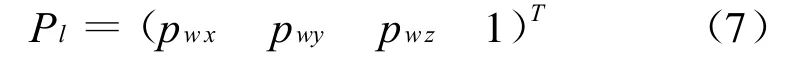
则理想运动的刀具成形点的位置约束方程为:

在超光滑加工机床中,由于进给系统有两个回转运动,为成形过程调整刀具与光学元件的相对姿态提供了条件,因此可以加工复杂的光学表面,为此也需要掌握和控制成形过程中的刀具姿态。为了描述刀具的位姿变化,在刀具上固定一个矢量,令其与刀具一起运动,然后考察该矢量的转动情况。设刀具上刀柄至刀尖两点间的矢量 →V在刀具坐标系中的表达式为:

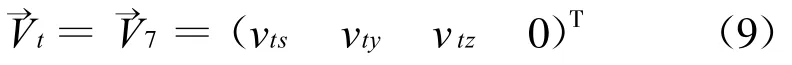
数控超光滑加工机床的特征矩阵见表2。

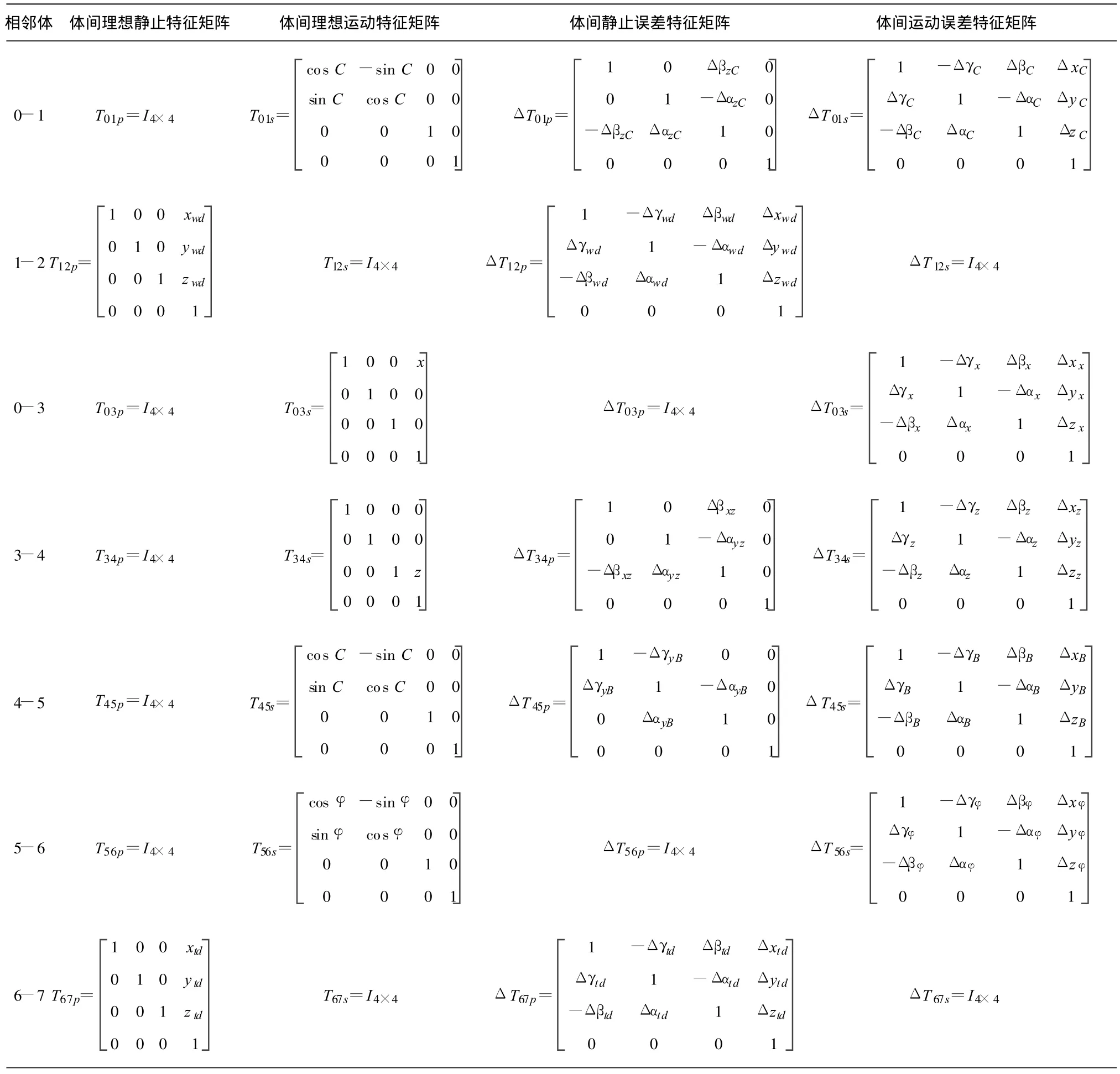
表2 数控超光滑加工机床的特征矩阵Table 2 Characteristic matrix of the CNCsuper-smooth process machine

那么在理想运动条件下,矢量→V在工件坐标系中的表达式为:

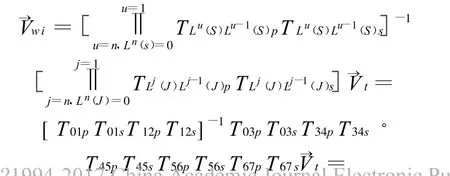
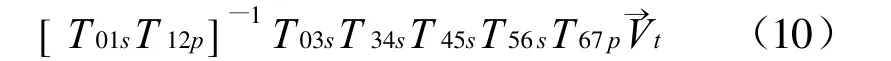
则理想运动的刀具姿态约束方程为:

刀具成形点在工件坐标系内的实际成形函数为:

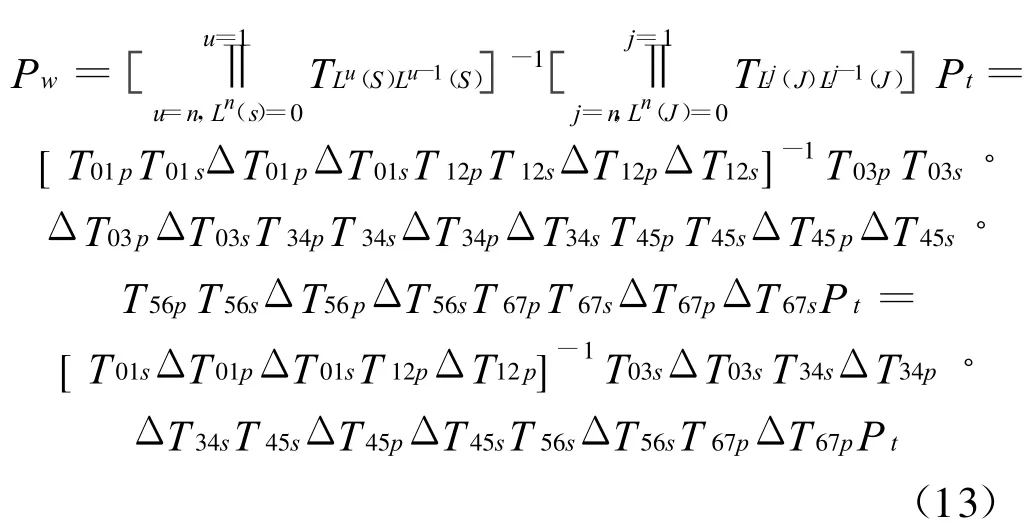
实际运动的刀具成形点的位置约束方程为:

在实际运动条件下,矢量 →V在工件坐标系中的表达式为:

则实际运动的刀具姿态约束方程为:

在实际成形运动中,刀具成形点的实际位置不可避免地会偏离理想位置,产生空间位置误差。刀具成形点的综合空间位置误差即为:

在实际成形运动中,实际刀具姿态也会不可避免地与刀具理论姿态存在偏差,这种偏差可以用与的矢量差来描述,这里用表示,因此刀具空间姿态误差即为:

式(18)即为超光滑加工机床的空间误差模型。

只需将表2中数控超光滑加工机床各体的特征矩阵代入空间位置误差模型的一般表达式,即可得到数控超光滑加工机床空间误差模型的具体表达式。在数控超光滑加工机床加工控制和误差补偿中的目标就是使抛光磨头(即刀具)中心点的实际位置尽可能地接近理想位置以及抛光磨头的实际姿态尽可能地接近理想姿态,亦即E和→E尽可能小。

4 结 论

基于多体系统运动学理论,建立了数控超光滑加工机床成形系统的低序体阵列,并推导出机床相邻体的特征矩阵,它是进行机床精度分析与建模的核心。基于多体系统运动学理论精度分析理论,详细研究了数控超光滑加工机床成形运动函数、成形运动约束、综合空间误差的建模过程,给出了具体模型表达式。基于多体系统理论的数控机床成形运动和误差分析和建模方法,全面考虑了影响机床加工精度的各项因素以及相互耦合情况,以低序体阵列来描述复杂系统,使运动学建模过程具有程式化、规范化、约束条件少的特点,易于解决复杂系统运动问题。

[1]JUNG B,JANG K I,MIN B K,et al.Magnetorheological Finishing Process for Hard Materials Using Sintered Iron-CNT Compound Abrasives[J].International Journal of Machine Tools&Manufacture,2009,(49): 407-418.

[2]CARL ZEISS SMT AG.Ion Beam Figuring for Lithography Optics[J].Nuclear Instruments and M ethods in Physics Research Section B:Beam Interactions with Materials and Atoms,2009,267(8-9):1 390-1 393.

[3]施春燕,袁家虎,伍 凡,等.冲击角度对射流抛光中材料去除面形的影响分析[J].光学学报,2010, 30(2):513-517.

[4]刘又午.多体动力学的休斯敦方法及其发展 [J].中国机械工程,2000,11(6):601-607.

[5]粟时平.多轴数控机床精度建模与误差补偿方法研究[D].长沙:国防科学技术大学,2002.