优化的CT图像配准方法的研究与比较

金 英

(黑龙江大学 计算机科学技术学院,哈尔滨 150080)

0 引 言

医学图像配准[1]通过空间变换使两幅图像的对应点在空间位置上一致,配准的结果应使两幅图像上所有关键解剖点或感兴趣的点达到匹配。

在医学上,不仅有反映人体生理结构信息的CT、核磁共震(MR)等技术,而且有描述人体功能及代谢信息的正电子放射技术(PET)及单光子影像(SPECT)等先进手段和方法。由于不同的医学影像通常反映不同的、互补的和部分重叠的信息,综合利用多次成像或多种模式成像可以获得较全面的信息,使临床诊断和治疗、放疗的定位和计划设计、外科手术和疗效评估等更加全面和精确。

图像配准的基本过程见图1。首先提取图像的特征信息组成特征空间,根据提取的特征空间选取一种空间几何变换,使一幅图像经过变换后能够符合所定义的相似性测度。在选取变换过程中需要采取一定的搜索优化策略,使相似性测度更快、更准确地达到最优值。

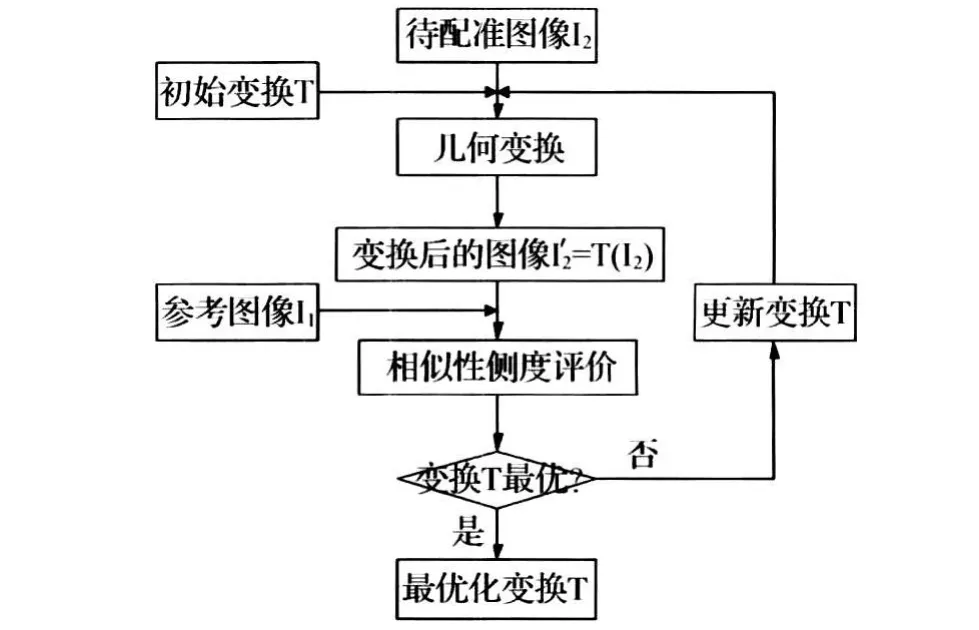
图1 图像配准的基本流程Fig.1 Flowchart of registration procedure

由于医学图像配准在医学研究与临床实践中具有重要的意义,近30年来国内外学者对其已进行了广范而深入的研究。配准的好坏可由两幅图像上的对应特征间的几何距离或图像间的像素浓度值之差来度量。对应地,可将图像配准分为基于特征的配准和基于像素浓度值的配准[2-3]。基于几何特征的图像配准具有运算速度快的优点,但该类配准通常需要进行特征提取方面的预处理工作,可能使算法的精度受到影响。能否自动而精确地提取特征是当前面临的一个挑战。基于像素浓度值的图像配准具有充分利用所有信息、不需要进行图像分割等预处理的优点而使得该类图像配准算法具有较高的配准精度,但存在配准速度慢的缺点。为了提高配准的精度和速度,人们提出了多分辨率配准方法。在多分辨率配准模式中,低分辨率层的配准为高分辨率层的配准提供了较好的初始估计值,从而避免陷入局部极值,并能提高运算的速度[4-5]。

尽管人们已经提出了许多图像配准方法,但是到目前为止还没有一个能应用于临床的通用的医学图像配准方法。本文通过实验对基于互信息的配准方法进行了广泛的研究与比较,从而找出更适合CT医学图像的配准方法。

1 关键技术

1.1 基于互信息的相似性测度

基于互信息(MI)的配准方法是将两幅图像看成两个离散随机变量,两幅图像可能来自不同的成像设备,但它们基于共同的人体解剖信息,所以当两幅图像的空间位置达到一致的时候,其中一幅图像表达的另一幅图像的信息,即互信息应为最大。因而,可将互信息作为相似性测度,通过寻求使互信息达到最大的变换参数来实现配准。互信息的数学表达式如下:

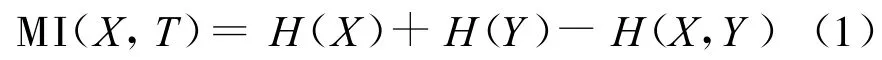
x,y分别为图像X,Y对应像素的灰度;pX(x),pY(y)以及pXY(x,y)分别为两幅图像重合部分的边缘概率分布以及联合概率分布。

在实际应用中,一般用概率分布来表示互信息,即:

由于最大互信息法对待配准图像间覆盖程度变化较敏感,有时会误配准[6]。为了提高互信息对图像重叠面积的稳定性,Studholme最早提出了归一化互信息(NMI)配准法,归一化互信息的表达式如下:

对齐度不好时,边缘熵增加,联合熵也会增大,归一化互信息量就不是最大。归一化互信息的最大化就是寻找一种变化使得联合熵相对于边缘熵最小,既考虑到了配准时联合熵较小,又考虑到了重叠区域内图像的信息,很好地平衡了两者之间的关系,从而使配准更具鲁棒性。

1.2 基于B样条的多分辨率配准

根据图像配准算法中对图像变换方式的不同可将其分类为刚体配准算法和弹性配准算法。刚体变换可以简单地用矩阵表示,其运算效率较高。刚体图像配准用于纠正由于旋转和平移而引起的图像失真,经常用于脑部图像的配准。对于腹部、肺部等组织或器官容易发生复杂变形或位移的部分,弹性配准比刚体配准更适合。但是由于组织或器官的变形或位移难以确定,目前使用的弹性配准算法配准误差较大。此外,由于运算的复杂性,弹性配准算法的运算速度也较慢。

基于B样条的变换是一种自由变换方法,其基本思想是将一个物体放入网格中,并使物体依据网格的变换而变换[8-9]。基于B样条的变换通过一些控制点操纵网格,因而很自然地能应用它进行多分辨率配准[10-13]。

在本文中,多分辨率配准金字塔的各层是通过设置不同层次的B样条控制点形成的,配准过程采用由粗到精的策略,见图2。

图2 基于B样条的多分辨率配准Fig.2 Multiresolution registration based on B-spline

1.3 优化算法

图像配准实质上是一个多参数优化问题,即寻找相似性测度达到最大时的空间变换参数。因此,图像配准过程实际上是配准函数优化过程,优化算法的选择将直接影响配准的精度和速度。医学图像配准中常用梯度下降法[13]和单纯形法[14]进行优化。在本文中,将通过实验对比这些方法在多分辨率配准中的性能。

2 实验结果及分析

本文在脑部与腹部的CT图像上进行实验与比较,从而寻找更优化的配准模式。首先,在脑部CT图像上基于全局仿射变换对相似性测度与优化算法的不同组合进行实验与对比,从而找出最优的组合。在此基础上做基于B样条的配准实验,本文中采用的配准实验基本框架见图3。

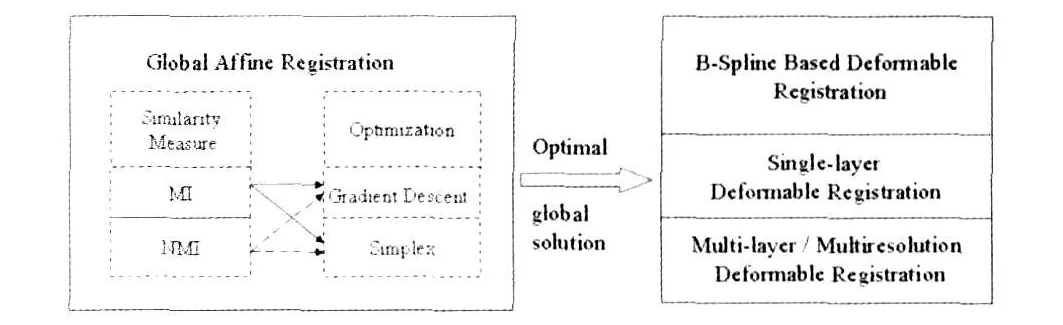
图3 配准实验框架Fig.3 Framework of registration experiments

2.1 全局仿射配准

为了评估配准性能,先在CT图像上进行变换,从而人工地产生浮动图像,之后将原图像与新产生的浮动图像进行配准,以获得配准的基本数据。在 x轴与y轴上的平移变换参数属于 [0, 15]区间,尺度变换参数属于 [0.8,1.2]区间。

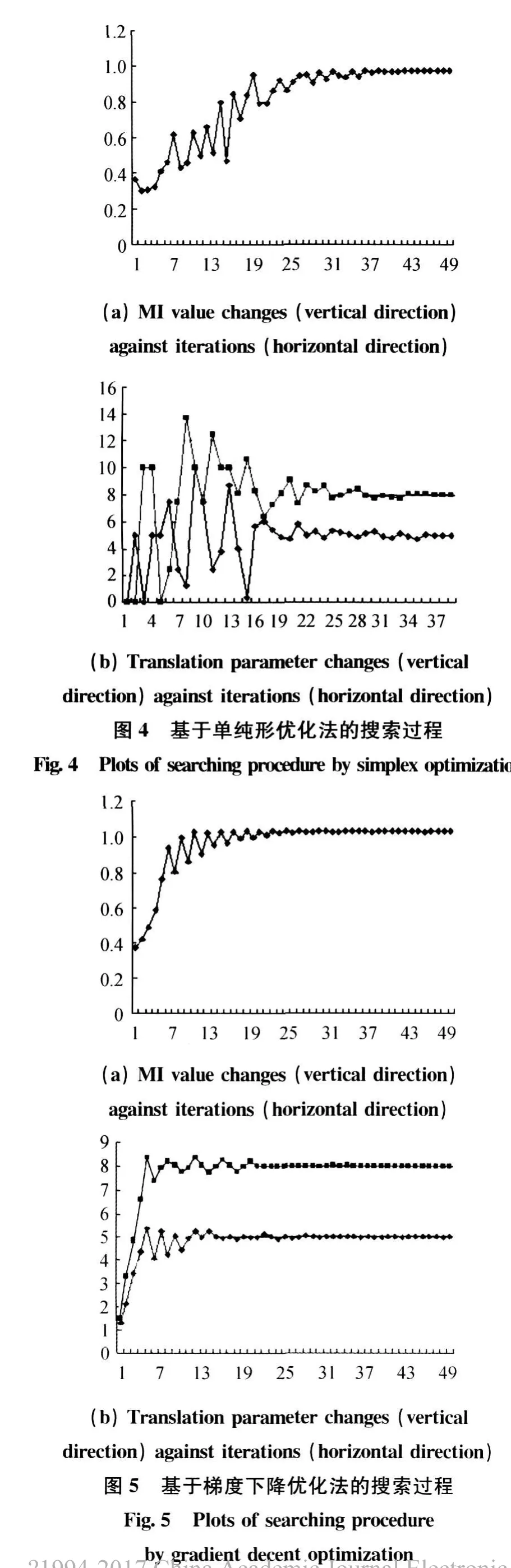
1)评估配准优化算法:通过进行一系列的实验,找出更好的CT图像配准的优化方法。图4和图5分别显示了基于单纯形法与梯度下降法的优化搜索过程及其相应的互信息值变化情况。

图4表明单纯形法能够在较广的范围进行优化搜索,因而不容易陷入局部极值。相对地,梯度下降法搜索优化参数的过程比较稳定也比较缓慢,见图5。实验表明,单纯形法在配准迭代与耗时方面优于梯度下降法。在CT脑部图像上所做的实验还表明作为图像配准的相似性测度,NMI优于MI。

2)仿射配准结果:为了验证和判断,我们进行了大量的实验。在本文中给出了两个配准结果示例,见图6。图6中的(a)、(b)、(e)、(f)是配准过程的输入图像。其中,浮动图像 (study image)是通过对参考图像 (reference image)进行简单的平移而得到的。图6中的 (c)是由图像(a)和(b)叠加得到的图像;而图6中的(g)是对图像(c)和(d)作差运算得到的图像;图6中的(d)和(h)是配准结果。从上述两种情况可以发现NMI和单纯形法的结合能产生满意的结果,因而可将其用于复杂弹性配准的初始化。

Case 1:

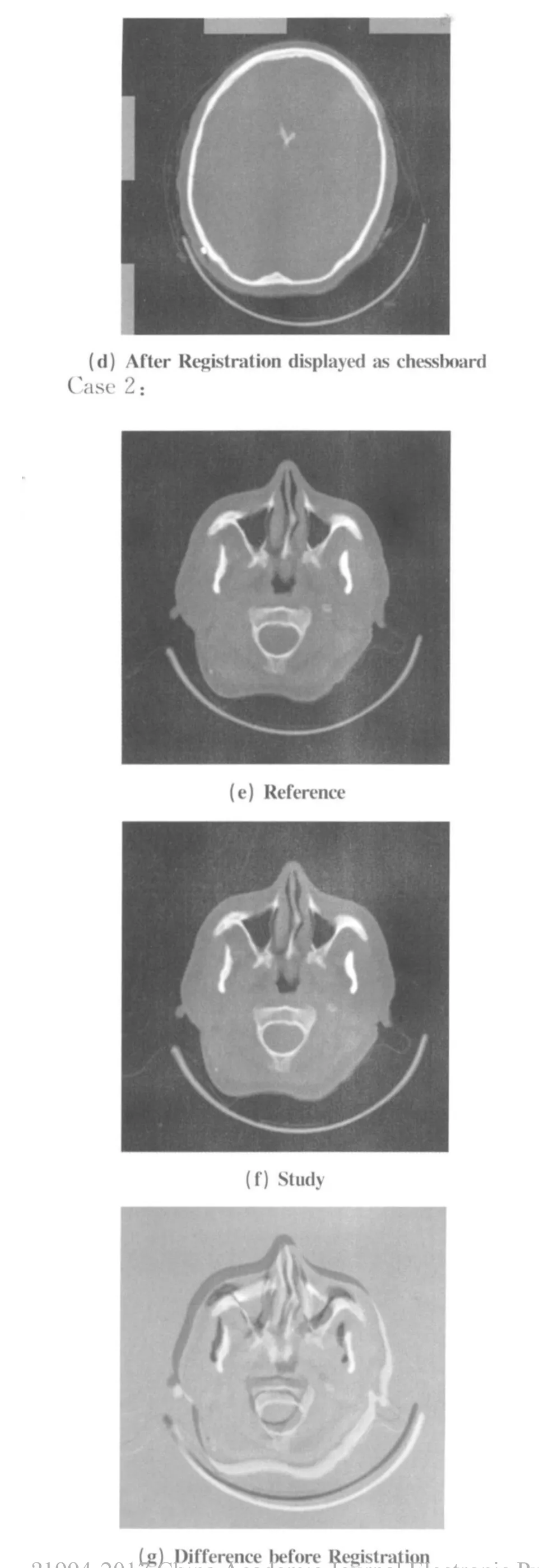
图6 仿射变换结果示例Fig.6 Experimental results of affine registration

2.2 基于B样条的不同个体间CT图像的弹性配准

为了构建基于特定人口的标准图谱或为了在数据库中查询相似疾病的医学图像,需要对不同个体的医学图像进行配准。然而,不同个体间其组织结构从形状、大小到体积等都有很大的差异,因而给图像配准带来了巨大的挑战。

1)弹性配准:本文对不同个体间CT图像进行了基于B样条的弹性配准。图7显示了一些弹性配准过程的结果。

图7(a)和(b)分别是来自不同个体的CT脑部参考图像与浮动图像;图7(c)是配准前参考图像与浮动图像的差;图7(d)是弹性配准后参考图像与经过变换的浮动图像的差。从这些图像不难发现,经过基于B样条的弹性配准后,取得了更佳的效果。

图7 基于B样条的弹性配准结果Fig.7 B-spline based deformable reigstration

2)比较实验:通过实验对单层 (原始图像分辨率)的弹性配准和多层(多分辨率)的弹性配准进行了比较。实验结果(图8)表明,多分辨率的配准比单分辨率配准具有更高的精度。多分辨率配准方法能够捕捉到更广范围的形变,并且由于在较低分辨率层为较高分辨率层提供了较好的参数初值,因而多分辨率配准方法收敛得更快。

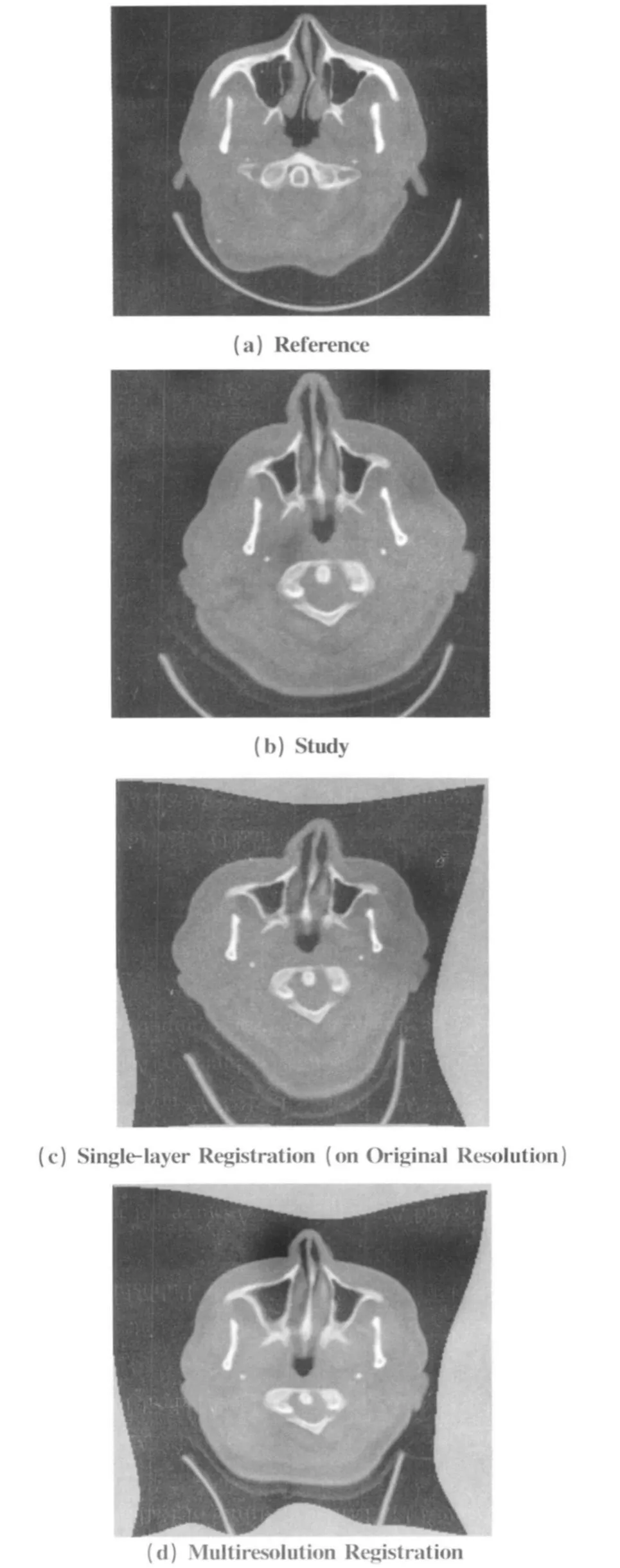
图8 基于B样条的单层弹性配准与多分辨率弹性配准比较试验Fig.8 Experimental comparion of single-layer deformable egistration and multiresolution registration based on B-Spline

3 结 论

本文研究与分析了对CT医学图像的仿射配准与基于B样条的弹性配准。实验表明,对于仿射配准,用NMI做相似性测度,用单纯形法作为优化算法会产生更好的结果。对不同个体的CT医学图像所进行的实验表明,多分辨率配准模式在精度与效率方面都优于单层的配准,并且能够处理更广范围的形变及不同个体间的差异。此外,若用优化的全局仿射配准做预处理,复杂的弹性配准会产生更好的结果。

[1]Hallpike L,Hawkes D J.Medical Image Registration: an Overview[J].British Institute of Radiology,2004, 14(6):455-463.

[2]M aintz,J.B.A.&Viergever,M.A.A Surey of M edical Image Registration[J].Medical Image Analysis,1998,2(1):1-36.

[3]Wang X.Y,S.Eberl,M.Fulham,et al.Data Registration and Fusion[M].Elsevier Publishing,2008, 187-210.

[4]Lester H.and Arridge S.R.A Survey of Hierrarchical Non-linear Medical ImageRegistration[J].Pattern Recognition,1999,32:129-149.

[5]Pluim J.P.W.,Maintz J.B.A.and Viergever M. A.Mutual Information Matchingin Multiresolution Contexts[J].Image and Vision Computing,2000,19 (1-2):45-52.

[6]Studholme,C.Measures of 3D Medical Image Alignment[D].London:UK.University of London,1997.

[7]Studholme,D.L.G.Hill and D.J.Hawkes.An O-verlap Invariant Entropy Measure of 3D Medical Image Alignment[J].Pattern Recognition,1999,32(1): 71-86.

[8]Mattes,D.Haynor,D.R.,Vesselle,H.,Lewellen,T.K.,et al.PET-CT Image Registration in the ChestUsingFree-Form Deformations[J]..IEEE Transaction on Medical Imaging.2003,22(1):120-128.

[9]Thévenaz,P.&Unser,M.Optimization of Mutual Information for Multiresolution Registration[J].IEEE Transaction on ImageProcessing,2000,9(12): 2 083-2 099.

[10]Unser,M.,Aldroubi,A.F.Multiresolution Image Registration Procedure Using Spline Pyramids[C]// Wavelet Applications in Signal and Image Processing, ed.Laine,A,Nov 1993 Proc.of SPIE(2034),160-170.

[11]Thévenaz,P.,Ruttimann,U.E.,&Unser,M.A Pyramid Approach to Subpixel Registration Based on Intensity[J].IEEE Transactions on Image Processing,1998,7(1):1-15.

[12]Thévenaz,P.,Ruttimann,U.E.,&Unser,M.“Iterative Multi-scale Registration Without Landmarks [C]//IEEE International Conference on Image Processing,Washington D.C.,1995:228-231.

[13]Brigger,P.,Muller,F.,Illgner,K.,et al.Centered Pyramids[J].IEEE Transactions on Image Processing,1999,8(9):1 254-1 264.

[14]Christensen,G.E.,Kane,A.A.,Marsh,et al. Synthesis of an Individualized Cranial Atlas with Dysmorphic Shape[C]//IEEE Proceedings of Mathematical Methods in Biomedical Image Analysis.1996: 309-318.

[15] Hédi,N.An Overview on the Simplex Algorithm [J].Applied Mathematics and Computation.2009, (210):479-489.