一类非线性广义随机系统的降阶Kalman滤波器

石 莹,田英明,田行伟

(黑龙江大学 电子工程学院自动化系,哈尔滨 150080)

0 引 言

广义系统(也称微分-代数系统)出现在电网络、化工过程、机械系统计算机辅助建模、航空航天等领域。自20世纪70年代被提出以来广义系统理论已逐渐发展成为现代控制理论的一个独立分支,研究工作经历了从线性到非线性、从连续到离散、从确定性到不确定性、从无时滞到时滞等各个专题[1-4]。

针对非线性系统的状态估计问题主要有3种方法[5]:扩展Kalman滤波(EKF)、无迹Kalman滤波(UKF)和粒子滤波。3种方法中粒子滤波的精度最高,从计算速度上看,EKF具有明显的优势。文献 [6]针对一类带有未知输入的非线性广义系统,利用UKF方法给出了状态和未知输入的估值器,并且不需要知道未知输入的先验信息。文献[7]在文献 [6]的基础上,给出了观测含有状态的导数和代数的非线性广义系统的状态估值器。但上述方法都对状态方程进行了增广,加大了矩阵的维数,带来了一定的计算负担。

本文针对广义非线性系统,基于 Taylor级数展开对系统进行了线性化,利用奇异值分解对线性化后的系统进行了降维,最后利用经典Kalman滤波理论给出了递推的状态估计值器,便于工程实现,减少了计算负担。

1 问题的描述

考虑非线性广义随机系统:

其中状态变量x(k)∈Rn,观测y(k)∈Rm,M是奇异常数矩阵,rank M=r＜n。

假设1 系统噪声w(k)和观测噪声v(k)是零均值相关白噪声,即:

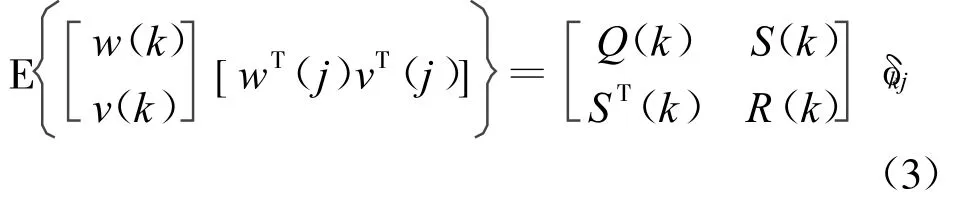
其中E为均值符号,T为转置符号,δkk=1,δkj= 0(k≠j)。

假设2 初始状态x(0)与w(k)和v(k)不相关,且

假设3 f(◦)和g(◦)是关于x(k)可微的。

假设4 广义系统(1)-(2)是强可控的[9]。

问题是:基于观测{y(0),…,y(k)}求状态x(j)的Kalman滤波器若j=k,称为状态滤波器,若j＜k,称k)为状态预报器。

2 模型的转化

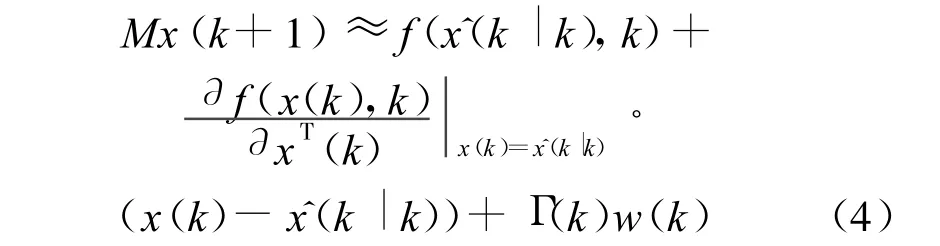
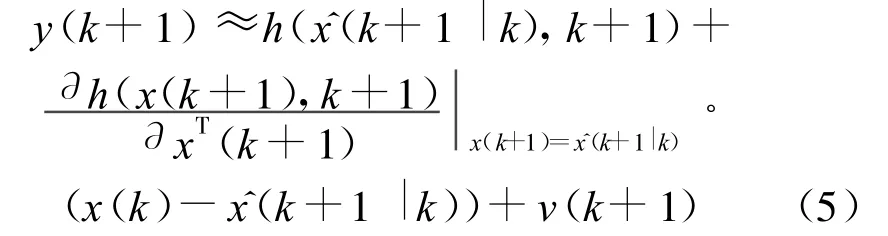
若令:

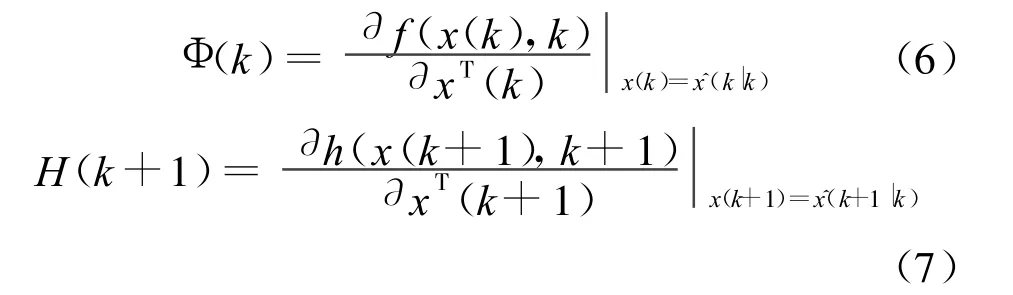
则式(4)-式(5)整理为:

这样就通过Taylor级数展开,将非线性广义系统(1)-(2)转化为线性广义系统(8)-(9)。

因为rank M=r,根据矩阵奇异值分解理论[10],存在正交矩阵U∈Rn×n,V∈Rn×n,使得:

式中 ∑=diag(σ1,σ2,…,σr);σi(i=1,2,…,r)是矩阵M的奇异值。

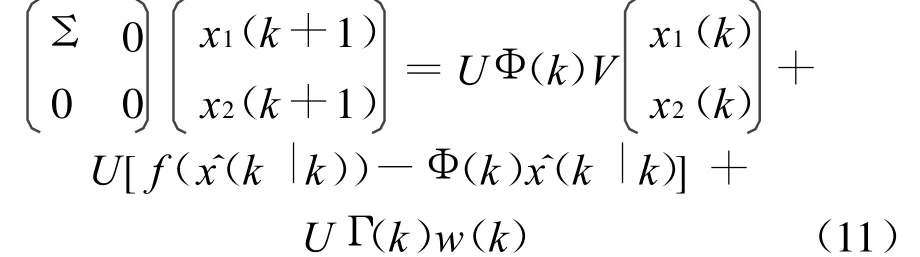
若A22(k)可逆,则式(12b)改写成:

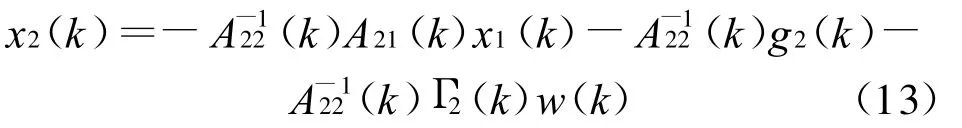
将式(13)代入式(12a)得到一个r维子系统:

其中:

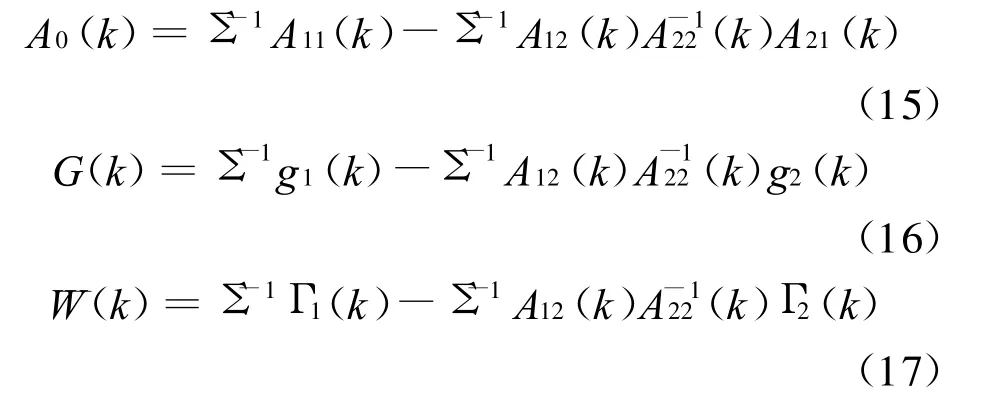
将式(13)代入式(9),整理得:

其中:

η(k)与w(k)的相关系数为:

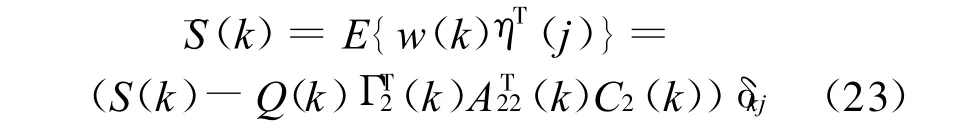
η(k)的方差阵为:

通过上面的分析,我们看到利用Taylor级数展开和奇异值分解,就将非线性广义系统(1)-(2)转化为了式(14)和(18)构成的正常等价系统。下面的工作就是利用经典Kalman滤波理论求解非线性广义系统的状态估值器。

3 状态Kalman滤波器

定理1 非线性广义系统(1)-(2)在假设条件1-4下,有降阶Kalman预报器为:

预报误差方差阵:

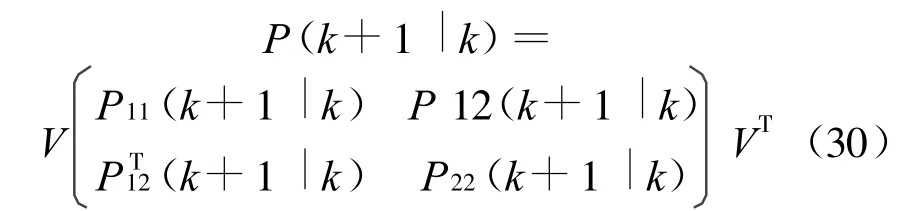
其中:

定理2 非线性广义系统(1)-(2)在假设条件1-4下,有降阶Kalman滤波器为:

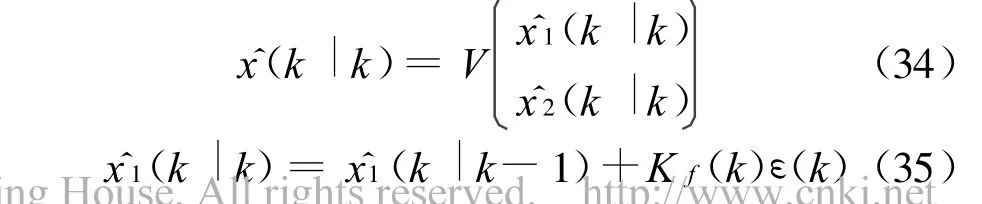
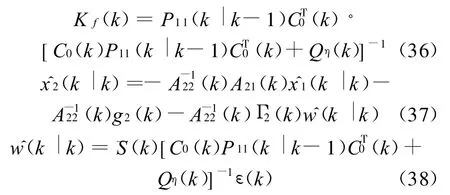
滤波误差方差阵:

4 数值仿真

考虑如下非线性广义系统模型:

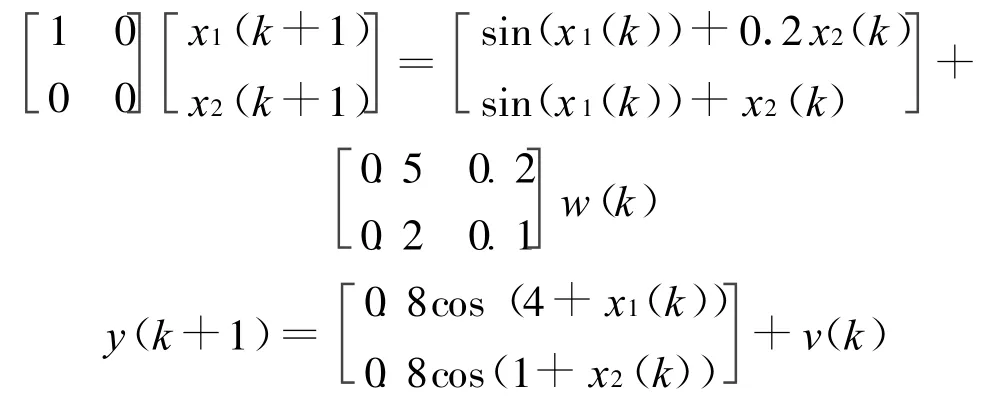
其中w(k)和v(k)是相互独立的白噪声,方差阵分别为 Q=diag[1,2],R=diag[0.81, 0.64]。x0=[0.1 0.1]T,P0=diag[1 000, 1 000]。利用定理1和定理2对状态进行Kalman滤波,仿真结果见图1和图2,图中实线为状态的真值,虚线为状态的Kalman滤波器。

图3和图4是状态与估值器的误差平方累积和比较图,实线是预报器,虚线是滤波器。从图中可以看出,滤波器与真值的误差平方累积和曲线在预报器的下方,表明滤波器的估计精度高于预报器,这与理论推导结果是一致的。

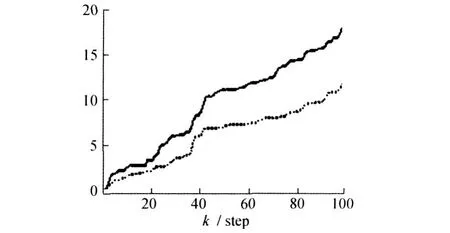
图4 第二个分量预报器和滤波器的误差累计和比较图Fig.4 Accumulated error sum comparison between predictor and fliter of the second component

5 结 论

本文针对一类非线性广义系统,在假设1～4下考虑了状态的线性最小方差估值问题。将状态方程在(k|k)处进行Taylor级数展开,观测方程在(k+1|k)处进行Taylor级数展开,实现了对非线性系统的线性化;再利用奇异值分解,将广义系统转化为等价的正常线性系统,基于Kalman滤波理论得到了状态的一步递推Kalman预报器和Kalman滤波器,并通过Matlab对所提出的算法进行了有效性验证,得到了与理论推导相一致的结果。

但本文只是对非线性广义系统状态估计问题的初步探讨,还有很多的工作需要进一步研究,例如初值选取对算法的收敛性的影响、线性化滤波方法的适用范围、矩阵A22(k)不可逆情况下如何求解等等。

[1] Rosenbrock H H.Structural Properties of Linear Dynamic Systems[J].Int.Journal of Control,1974,20 (2):191-202.

[2]Nikoukhah K,Willsky A S and Bernad B C.Kalman Filtering and Riccati Equations for Descriptor Systems [J].IEEE Transactions on Automatic Control,1992, 37(9):1 325-1 341.

[3]吴爱国,段广仁.广义线性系统基于PI观测器鲁棒极点配置分离原理 [J].应用数学,2007,20(4):771-776.

[4]高 媛,李怀敏,邓自立.带多层融合结构的广义系统Kalman滤波器 [J].自动化学报,2008,34(6): 639-646.

[5]刘双全,李修和,陈明建.非线性滤波算法分析及其性能比较[J].舰船电子对抗,2008,32(1):56-59.

[6]Shuwen Pan,Hongye Su,Zhitao Liu,et al.Unscented Kalman Filtering Approach for Nonlinear Singular Systems[C]//11th Int.Conf.Control,Automation,Robotics and Vision,Singapore,2010.

[7]V.M.Becerra,P.D.Roberts,G.W.Griffiths.Applying the Extended Kalman Filter to Systems Described by Nonlinear Differential-algebraic Equations[J].Control Engineering Practice,2001,9(3):267-281.

[8] RaviKumarMandela,Raghunathan Rengaswamy, Shankar Narasimhan,et al.Recursive State Estimation Techniques for Nonlinear Differential Algebraic Systems [J].Chemical Engineering Science,2010,65:4 548–4 556.

[9]张卓奎,陈慧婵.广义离散随机非线性系统的递推算法[J].西安电子科技大学学报:自然科学版,2007,34 (2):317-321.

[10]杨冬梅,张庆灵,姚 波.广义系统[M].北京:科学出版社,2004:16-21.