确定起重机合理回转速度的原则与方法

林贵瑜，张永刚，李伟亮

（1.东北大学 机械工程与自动化学院，辽宁 沈阳 110004；2.辽宁抚挖重工机械股份有限公司，辽宁 抚顺 113126）

起重机的回转速度参数是起重机总体参数中的1个重要参数，是决定回转功率的基本依据，其参数合理与否，既直接影响结构件的强度，又影响设备运行的平稳性.目前，国内对起重机回转速度的研究很少.国外的文献对回转机构也都是从源头进行详细的研究［1］，即建立多自由度机构的动力学模型，所需的源头数据很多，在初步设计阶段，这些数据是无法提供的，因此，此方法缺乏可操作性.在初步设计阶段方案分析中，拟从臂端吊重的偏摆角度出发，以非线性动力学的方法进行研究，从而确定各个运行机构运动参数的问题也未见有关文献介绍.在初步设计阶段制定方案中，设计者凭借自身的设计经验或参考已有的机型，选取回转速度，具有一定的主观性和便捷性，但缺乏设计的主动性.因此提出仅利用基本数据，能较满意地确定回转速度的1种方法.

1 确定回转速度的原则与方法

确定回转速度是在吊重回转过程中，以保证吊重物体的运动平稳性和整机动稳定性为原则，其方法是建立吊重与偏摆角的动力学模型和数学模型，取其中偏摆角的最小值并且小于规范值作为运动平稳性和整机动稳定性的度量值，相应的回转速度即为合理.

1.1 运动平稳性确定回转速度

运动平稳性是指由于起重机在回转启动或制动时吊重物体产生的切向惯性力和离心力，货物所受的风力，使悬吊物体的挠性钢绳对铅垂线将产生偏摆角φ［2］，见图1a，其值与回转速度有关.图中mp，F2分别为起重臂在顶部的等效质量和mp产生的离心力.

以上各力不是作用在同一平面和同一方向上，但是由于吊重物体来回摆动的周期长，衰减慢，在图1b中，吊臂处于位置A，回转机构启动，产生货物切向惯性力FQ.当吊臂旋转到位置B时，切向加速度引起吊重物体来回摆动有可能仍在原来的平面内继续进行，因而有可能使偏摆角代数叠加［3，4］.假定此时货物同时承受风载荷FF、切向惯性力FQ、离心力FL；计算得出吊重物体的最大偏摆角φ.

图1 回转机构计算简图Fig.1 Swiveling mechanism calculation diagram

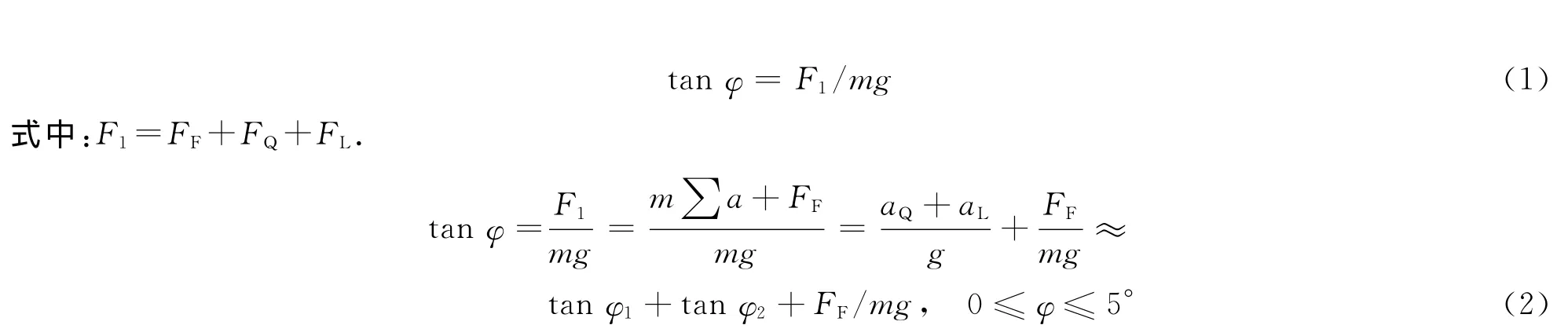
式中：m为吊重的质量，kg；a为总加速度，m·s-2；aQ为由FQ产生的切向加速度，m·s-2；aL为由FL产生的向心加速度，m·s-2；φ为吊重的总偏摆角，（°）；φ1为由离心力FL作用吊重产生的偏摆角，（°）；φ2为由切向惯性力FQ作用吊重产生的偏摆角，（°）.

现分别计算由离心力和切向惯性力引起吊重的偏摆角.

1.1.1 离心力产生的偏摆角

在回转时，吊重及起重机各转动部分在旋转时产生离心力FL，当转速为n1时的FL为［5］

式中：R为回转半径的长度，m.

悬挂在钢丝绳上的吊重，由于FL使钢丝绳向外偏斜角度φ1，使吊重的实际回转半径由R增为R1，

式中：ΔR1为FL作业半径的增量，ΔR1＝Lsinφ1，L为吊重钢绳长度；H为FL作用下，起重臂顶部距起吊重物重心的距离，m.

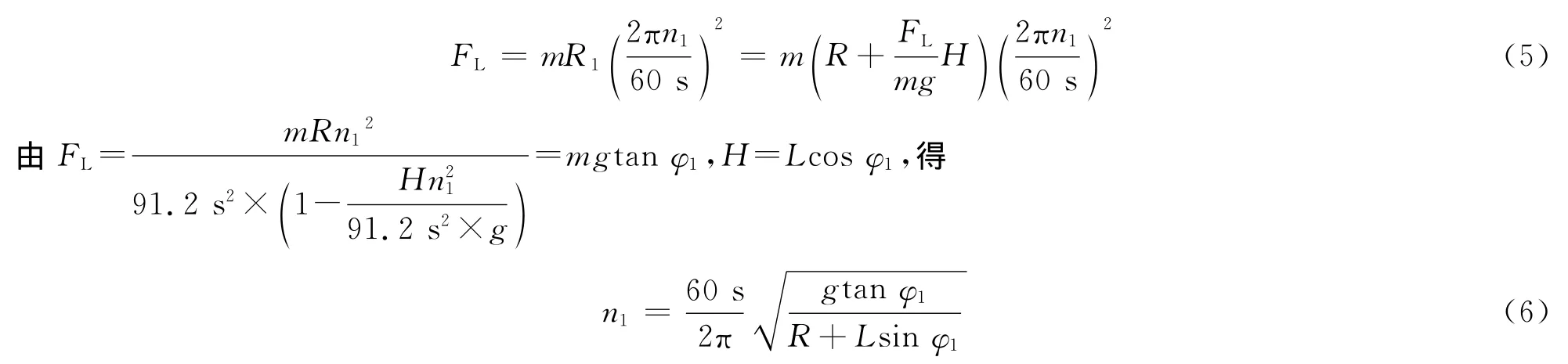
式中：n1为回转速度，r·min-1.

1.1.2 切向惯性力产生的偏摆角

在回转启动或制动时刻，吊重在起重臂头的切向惯性力FQ影响下将产生滞后的摆角φ2，作用在吊重上的FQ及φ2和mg，FQ之间的力学关系为

式中：t为回转启动（或制动）时间，s；ΔR2为FQ作用时回转半径的增量，m；H1为FQ作用下起重臂顶部距起吊重物重心的距离，m.

整理后得

若不考虑风载荷的影响，取L＝5m，t＝5s，R＝5，10m，解方程（6）和方程（8），得到FQ，FL，n1与φ的关系，如图2所示.

由图2可知，当回转半径R＝10m，转速n1＝2r·min-1时，FQ产生的吊重摆角φ2与FL产生的吊重摆角φ1之和φ＝5°；若转速n1＝1r·min-1时，φ＝2°，并保证吊重偏摆角φ≤［5°］的规范值，可根据图2选择合适的回转速度.

从转速计算公式和图2表明：回转转速值与吊重回转半径R成反比；回转转速愈高，其吊重摆角就愈大，运动愈不平稳，因此控制吊重摆角，就控制了回转转速，即控制了运动平稳性.

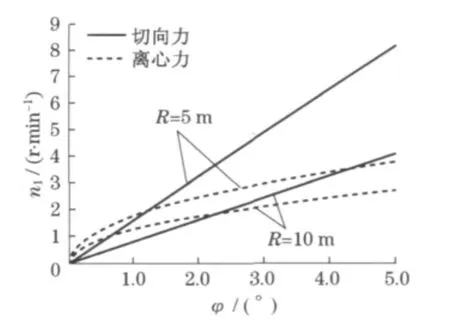
图2 回转转速n1与摆角φ的关系Fig.2 Relationship between rotating speed n1and deflection angleφ

1.2 整机动稳定性确定回转速度

整机动稳定性是指吊重在回转作业时在FQ，FL的作用下，增加了横向的倾翻可能性，其横向稳定性受到影响.所谓回转速度是指吊起额定载荷的重物并保证整机稳定性时的最高回转速度，其值是随着起重臂长度、额定载荷及作业半径的大小而变化.

额定载荷时的稳定条件为吊起相当于倾翻载荷的78%以内的重物；额定回转速度时的稳定条件为吊起相当于倾翻载荷的90%以内的重物.均需保证在静止时机器稳定［6］，此时认为在图1b所示水平位置，整机稳定性最差.

由于惯性力作用而产生的倾翻力矩的增量为

整机允许的倾翻力矩的增量为

式中：φ2为回转时允许的倾翻载荷的比率，φ2＝0.90（经验值）；φ1为额定总载荷与倾翻载荷的比率，φ1＝0.78（经验值）；L3为从回转中心至倾翻支点距离，指履带侧向的最小值，即从回转中心至支重轮的外缘中心的距离.

令ΔM1＝ΔM，得到与n2有关的高次非线性方程式为

将式（6）和式（8）中n1替换为n2即可得φ1，φ2与n2的关系，联立方程组（2），（6），（8），（11），并通过数值解可求得n2.

1.3 实例计算

以某履带起重机为例，最大额定载荷为1600kN，R＝5m，b＝2.264m，L＝5m，L1＝18m，L2＝1.4 m，L3＝2.61m，mp＝3.5t.分别按上述2种分析方法计算，按整机动稳定性计算，解非线性方程式（11），求得n2＝0.9234r·min-1≈1r·min-1；按运动平稳性计算，再由图2，求得对应的吊重偏摆角为1°时，n1＝1.2r·min-1.

2种方法的计算结果经比较n2＜n1，应同时满足整机动态稳定性和运动平稳性的设计准则，即取回转速度n2＝1r·min-1是安全的.经实际考核，中型起重机的回转速度多在0.8～1.2r·min-1.

2 结论

通过上述计算与分析，得出以下结论：

（1）回转速度与回转半径成反比、与吊重摆角成正比，是影响吊重物体运动平稳性的主要因素.

（2）整机动稳定性对回转速度的影响较大，是影响回转速度的决定性因素.

（3）建立以吊重物体的运动平稳性和整机动稳定性为原则的力学模型、以吊重摆角为考核指标，以求得最小的回转速度为设计值，对设计有指导意义，其方法正确.

［1］SATO K，SAKAWA Y.Modeling and control of a flexible rotary crane［J］.Int J Control，1988，48：2085-2105.

［2］杨长马癸.起重机械［M］.北京：机械工业出版社，1982.YANG Changkui.Lifting appliances［M］.Beijing：China Machine Press，1982.

［3］哈尔滨建筑工程学院.工程起重机［M］.北京：中国建筑工业出版社，1979.Harbin Institute of Architecture and Civil Engineering.Construction crane［M］.Beijing：China Architecture and Building Press，1979.

［4］石殿钧.工程起重机［M］.北京：水利电力出版社，1983.SHI Dianjun.Construction crane［M］.Beijing：Hydraulic and Electric Power Press，1983.

［5］张质文，刘全德.起重运输机械［M］.北京：中国铁道出版社，1983.ZHANG Zhiwen，LIU Quande.Hoisting and conveying machinery［M］.Beijing：China Railway Press，1983.

［6］张质文，虞和谦，王金诺.起重机设计手册［M］.北京：中国铁道出版社，1998.ZHANG Zhiwen，YU Heqian，WANG Jinnuo.Handbook of crane design［M］.Beijing：China Railway Press，1998.