分数布朗运动下的亚式期权定价

周 银， 杜雪樵

(合肥工业大学数学学院，安徽合肥 230009)

根据文献[6]中的wick积分，可得到(1)式的解为:

无风险折现利率为:

期权定价是金融数学中的核心问题之一，近年来，国际金融市场涌现出了大量的由标准期权变化、组合、派生而出的新品种，即新型期权[1]。亚式期权就是现代金融市场中广泛应用的一种新型期权，它的收益取决于有效期内某段时期的金融资产价格的平均值。

自从 Black-Scholes期权定价公式被提出后[2]，这一公式便被广泛地应用于金融市场的定价分析。但是这一传统公式是建立在有效市场假设之上的，而近年来对股票市场的大量研究结果均表明股票市场价格变化并不符合正态分布。而分数布朗运动正好具备长时间相关、自相似等特征，因此它能很好地刻画股票波动规律，文献[3]使用傅里叶变换法推导了基于分数布朗运动条件下Black-Scholes期权定价公式。

尽管亚式期权已经在实务界得到广泛应用，其定价公式仍没有从理论上得到较好的解决，文献[4]首次提出期权定价的保险精算方法，将期权定价问题转化为等价的公平保费确定问题，由于无任何经济条件假设，因此对有套利、非均衡、不完备的市场也有效;文献[5]在保险精算下用矩求亚式期权。本文在分数布朗运动的条件和期权保险精算定价模型的基础上得出了亚式期权的定价公式，仅考虑在固定敲定价格计算看涨期权，看跌类似可得。

1 预备知识

1.1 分数布朗运动

Mandelbrot和Van Ness首先研究了分数布朗运动，其定义如下:

定义1 定义的在某概率空间的随机过程{BH(t)，t≥0}为Hurst参数H∈(0，1)的分数布朗运动，若

(1)BH(t)以概率1连续，且BH(0)=0。

(2)对任何t≥0，h≥0增量BH(t+h)-BH(t)服从均值为0，方差为h2H的正态分布。

分数布朗运动是具有平稳增量的连续的零均值Guassian过程，满足E[BH(t)]=0，协方差为:

BH(t)的分布函数为:

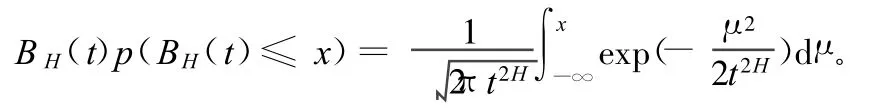
BH(t)为标准布朗运动B(t)时，H=1/2。

如果标的资产(股票)价格S(t)满足:

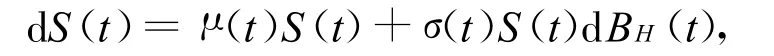
则称S(t)服从几何分数布朗运动，μ(t)、σ(t)分别代表风险资产价格的预期收益率与波动率，为了计算方便，假设μ(t)=μ，σ(t)=σ为常数，即

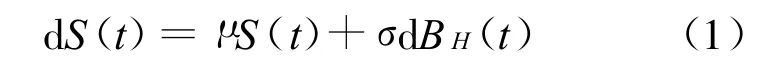
1.2 几何平均亚式期权的保险精算定价模型

考虑由2类资产组成的连续贸易金融市场，一类是在t时刻具有瞬间无风险利率为r(t)的无风险资产;另一类为风险资产(股票)，在t时刻其价格为S(t)，考虑的时间区间为[0，T]。0表示初始时间;T表示到期日;{S(t):t≥0}是在给定的完备空间(Ω，F，F(t)t≥0，P)上的随机过程，{F(t)t≥0}是由S(t)产生的子空间，假设S(0)=S是大于零的常数，有关保险精算定价的概念沿袭文献[4]。

定义2 随机过程 S(t):t≥0在[0，T]区间上产生的期望收益率∫t0β(s)d s被定义为:

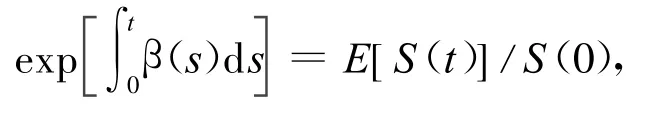
即有:eβt=E[S(t)]/S(0)。

其中，β(t)为t时刻S(t)的连续复利收益率。而且有:

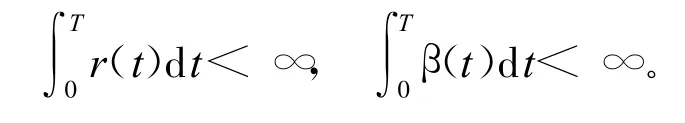
根据文献[6]中的wick积分，可得到(1)式的解为:

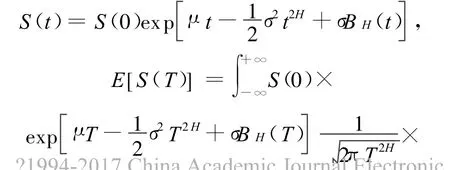
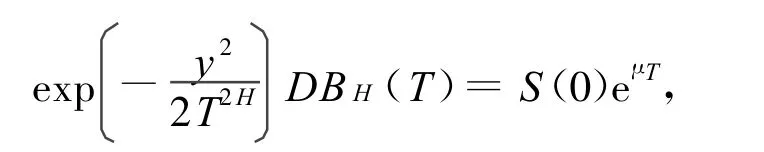
即有:eβT=E[S(T)]/S(0)=eμT。

设C(K，T)表示以股票价格S(t)为标的资产，执行价为K，到期日为T的几何亚式期权保险精算定价[7]，令

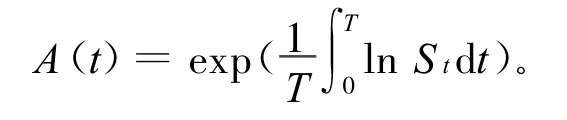
定义3 平均价格型亚式期权的保险精算定价为:当期权被执行时，在[0，T]内股价平均价格A(T)的折现值与执行价的折现值之差，在股票价格实际分布的概率测度下的数学期望[4]。资产折现值的计算方法如下:无风险资产(确定的)按无风险利率折现，风险资产(随机的)按其期望收益率折现。

几何平均亚式期权在到期日被执行的充要条件α是:

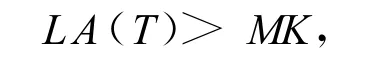
其中，期望收益折现率为:

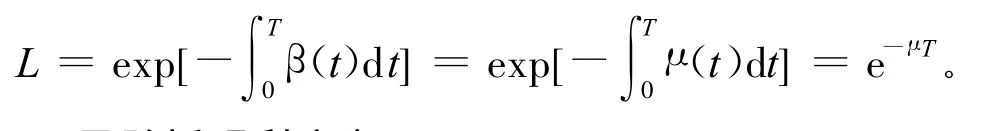
无风险折现利率为:

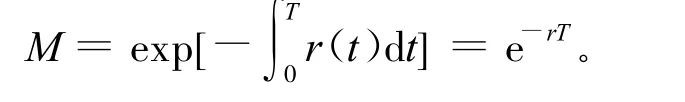
由定义3可知:

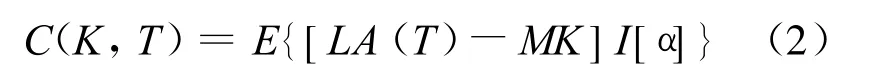
2 结 论

定理1 在分数布朗运动环境下，具有固定敲定价格的亚式看涨期权的价格为:

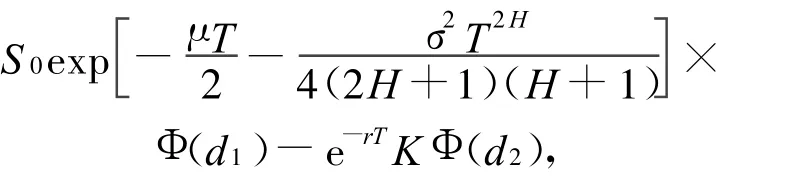
其中，d1=(¯μ+¯σ2-ln K-(μ-r)T)/¯σ=

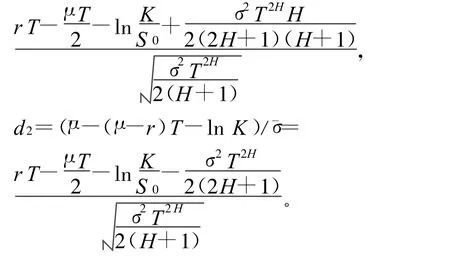
证明 由定义3有:

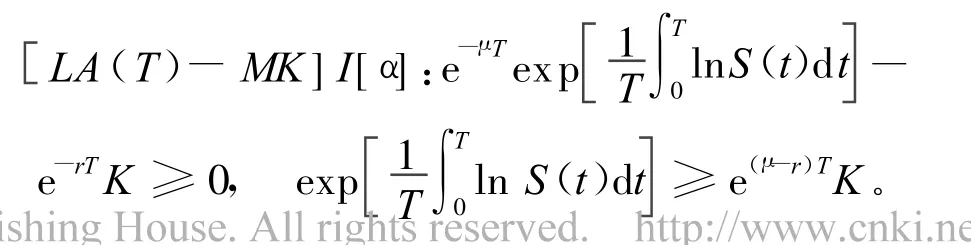
下面求出y的概率密度为:

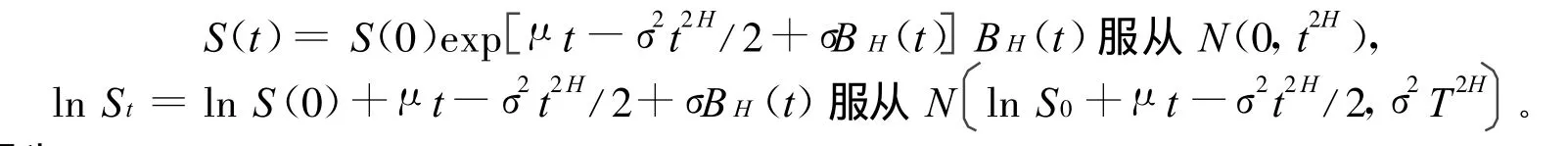
y的期望为:

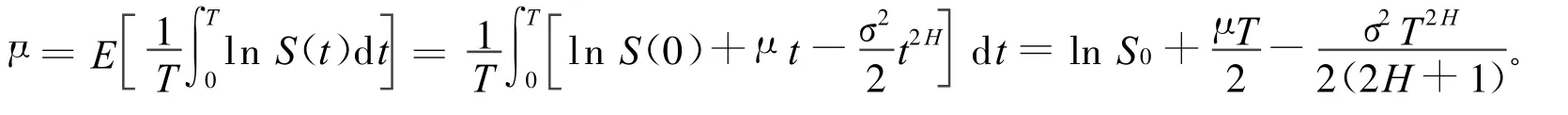
y的方差为:

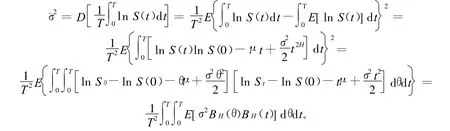
又因为:

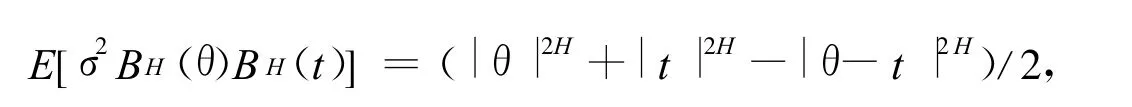
所以有:

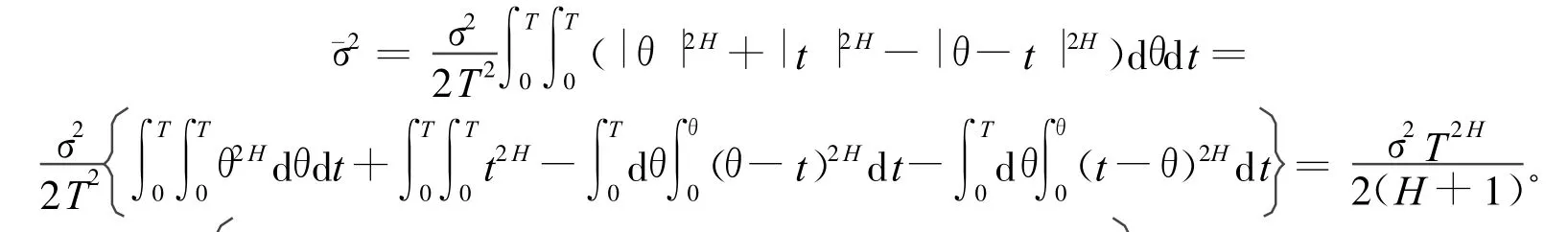
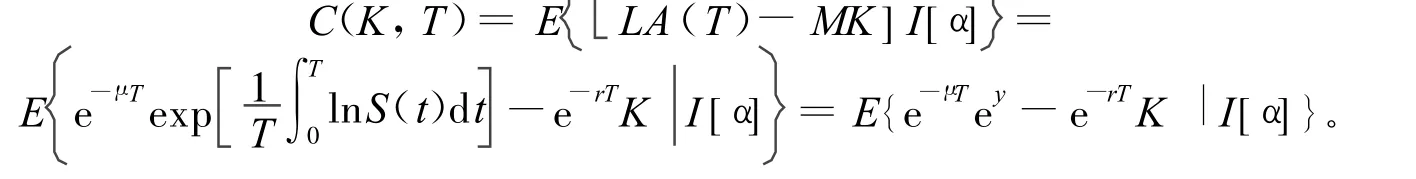
所以有:

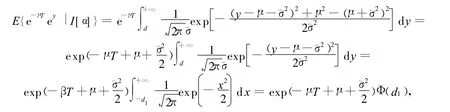
其中，d1=(¯μ+¯σ2-d)/¯σ=(¯μ+¯σ2-ln K-(μ-r)T)/¯σ。

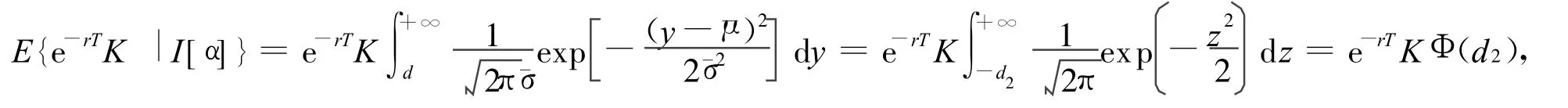
其中，d2=(¯μ-d)/¯σ=(¯μ-(μ-r)T-ln K)/¯σ。

综上所述，则有:

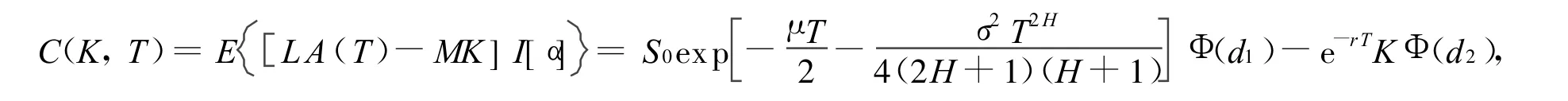
其中

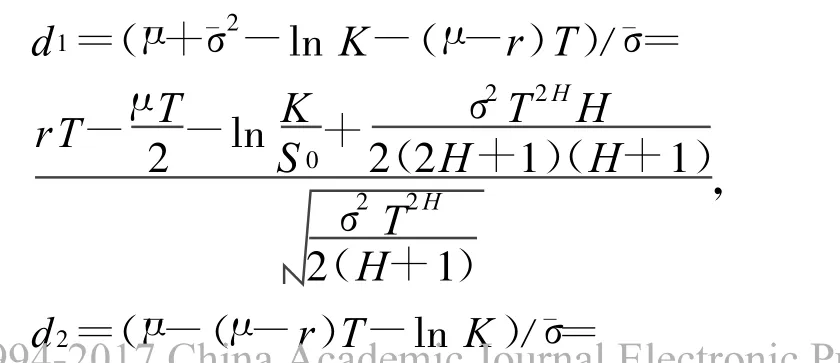
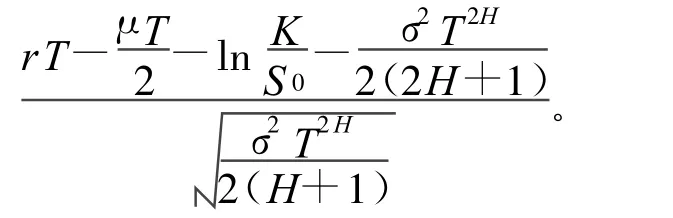
推论1 当μ=r，H=1/2时，即为标准布朗运动环境下，在风险中性的条件下得出的几何平均亚式看涨期权定价公式为:

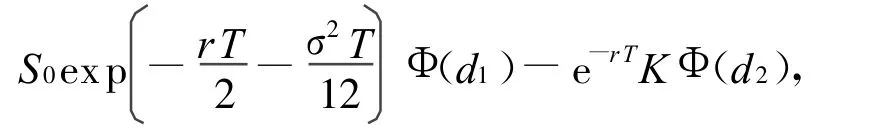
此定价公式与文献[8]中的结论相同。

分数布朗运动比传统的Black-Scholes期权公式更能解释资本市场中的价格变化现象。和推论相比，分数布朗运动下保险精算的方法模型能在更宽广的范围内使用，是对其在标准布朗运动下和风险中性条件下极大的推广，表现出了本文的合理性，可见标的资产服从标准布朗运动下的几何亚式期权定价是分数布朗运动下的一种特例。分数布朗运动比传统的Black-Scho les期权公式更能解释资本市场中的价格变化现象。在几何分数布朗运动中，期权的价值不仅与资产价格S、时刻T和t有关，而且由于股票价格的变化具有长相关性，因此期权的价值还应与Hurst参数H有关。

[1] 约翰◦赫尔.期权、期货和衍生证券[M].张陶伟，译.北京:华夏出版社，1997:450-463.

[2] Black F，Sholes M.The p ricing of options and corpo rate liabilities[J].Journal of Political Econom y，1973，81(4): 633-654.

[3] Necu la C.Option p ricing in a fractional B row nian motion enviroment[EB/OL].(2002-02-12)[2009-12-20].http:// ssrn.com/abstract=1286833.

[4] Bladt M，Rydbert T H.An actuarial app roach to option p ricing under the phy siclmeasu re and w ithoutmarket assum ptions[J].Insurance:Mathematics and Econom ics，1998，22 (1):65-73.

[5] 叶小青，蹇 名，吴永红.亚式期权的保险精算定价[J].华中科技大学学报:自然科学报，2005，12(3):91-93.

[6] Hu Y，Ksendal B.Fractionalw hite noise calculusand applications to finance[J].Infinite Dimensional Analysis，Quantum Probability and Related Topics，2003，6:1-32.

[7] 姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社，2003:277-294.

[8] 章 珂，周文彪.几何平均亚式期权的定价方法[J].同济大学学报:自然科学版，2001，29(8):924-927.