解非线性方程的一类多参数迭代格式
2011-03-15陈小惠
陈小惠, 唐 烁
(合肥工业大学数学学院,安徽合肥 230009)
0 引 言
在科学研究或工程技术领域中,常常会遇到许多实际问题的数学模型,例如非线性力学问题、电路问题、经济和非线性规划问题等,它们最终都归结为非线性方程f(x)=0,x∈R的求解问题,因此研究和解决非线性方程解的存在性及寻求其有效数值解法都是非常必要的。迄今为止,解非线性方程的方法很多,通常使用的是牛顿迭代方法及其改进方法,另外还有很多通过其它方法构造的迭代方法[1-8]。这些方法中有些阶数已经达到8阶,但是其迭代形式比较复杂,所以本文基于Chebyshev-Halley公式,给出了一个多参数迭代方法,在一定条件下该方法至少是3阶收敛的,且形式简单。实例说明了该格式的有效性与优越性。
著名的Chebyshev-Halley公式[4]为:
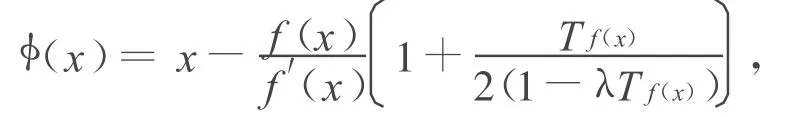
其中,Tf(x)=f(x)f″(x)/[f′(x)]2;λ为一个任意的实参数。该方法是3阶收敛的,λ=0时为Chebyshev方法;λ=1/2时为Halley方法;λ=1时为Super-Halley方法;λ→±∞时为经典New ton方法。
本文在Chebyshev-Halley公式的基础上,构造了一类不需要计算2阶导数的双参数迭代方法,且在一定条件下可以达到4阶收敛。
1 迭代公式的构造
为了减少2阶导数的计算,本文引入参数β(β为任意非零实数),将Chebyshev-Halley公式做如下的修改,即
令y=x-βf(x)/f′(x),β为任意非零实数,将f(y)Taylor展开为:
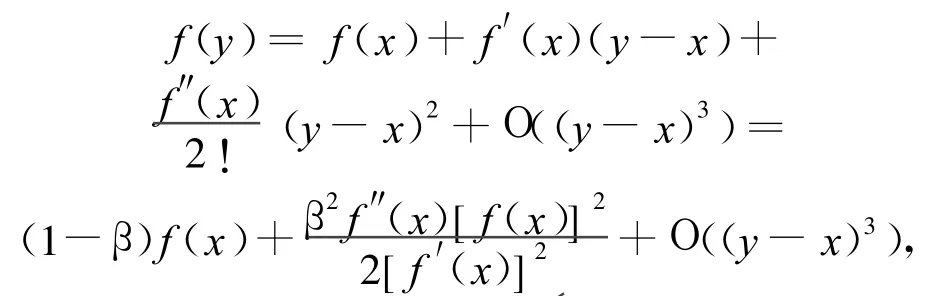
可得:
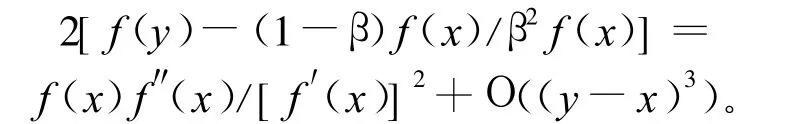
从而将
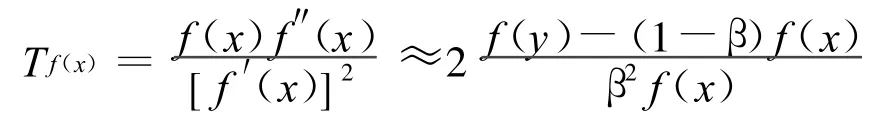
代入Chebyshev-Halley公式得:
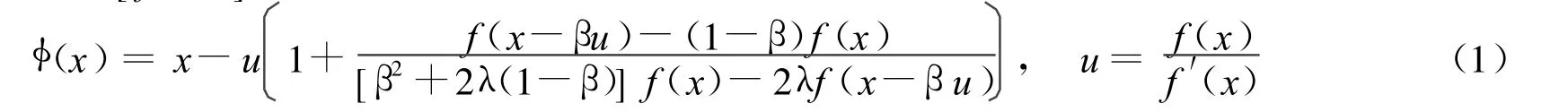
(1)式是依赖于参数λ和β的,以下给出一些特殊情况的迭代格式:
(1)当λ=0,β≠0时,

当β=1时,
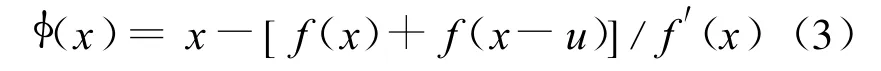
则(3)式为J.F.Traub给出的3阶收敛公式,见文献[9]。
当β=-1时,
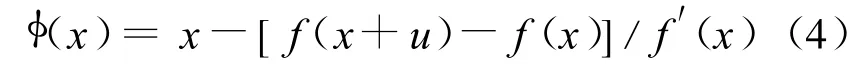
则(4)式为文献[5]给出的一个迭代公式,也是3阶收敛的。
当β→±∞时,
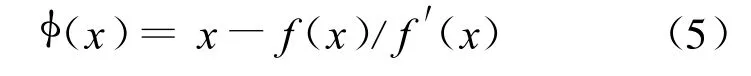
则(5)式为经典的New ton公式,它是2阶收敛的。
(2)当λ=β≠0时,
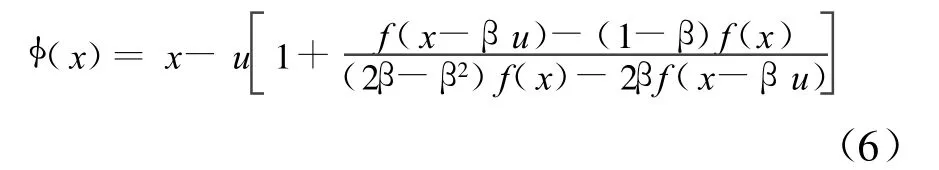
当λ=β=1时,
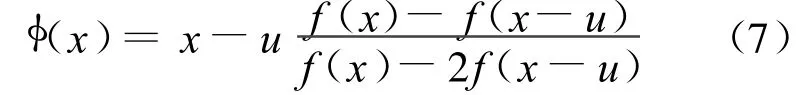
则(7)式为T raub-Ostrow ski格式,是4阶收敛的,见文献[4]。
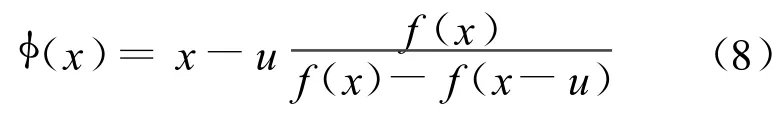
则(8)式为New ton-Secant格式[4],也是3阶收敛的。
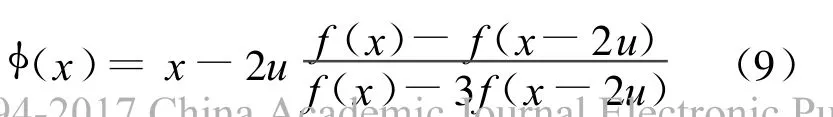
则(9)式也是3阶收敛的,证明见定理1。
2 收敛性分析
定义1 设序列{xk}收敛到α,记ek=xk-α,若存在实数p≥1及常数c>0,使则称序列{xk}是p阶收敛的[10]。
定理1 设f:A→R,在A中连续且有足够高阶的导数,如果f(x)有一单根α∈A,则在α足够近的邻域内,(1)式有如下收敛情况:
(1)当(λ,β)≠(1,1)时,3阶收敛;
(2)当(λ,β)=(1,1)时,4阶收敛。
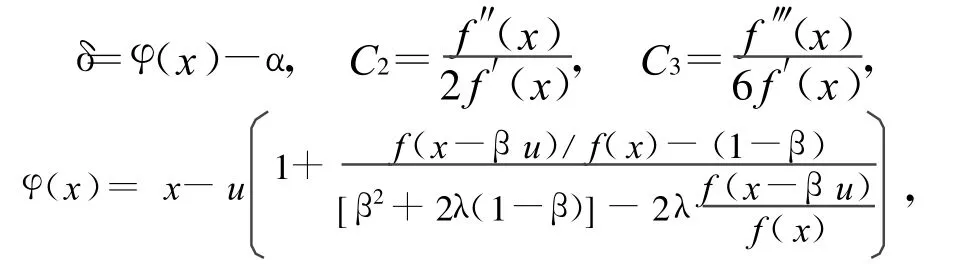
则有:
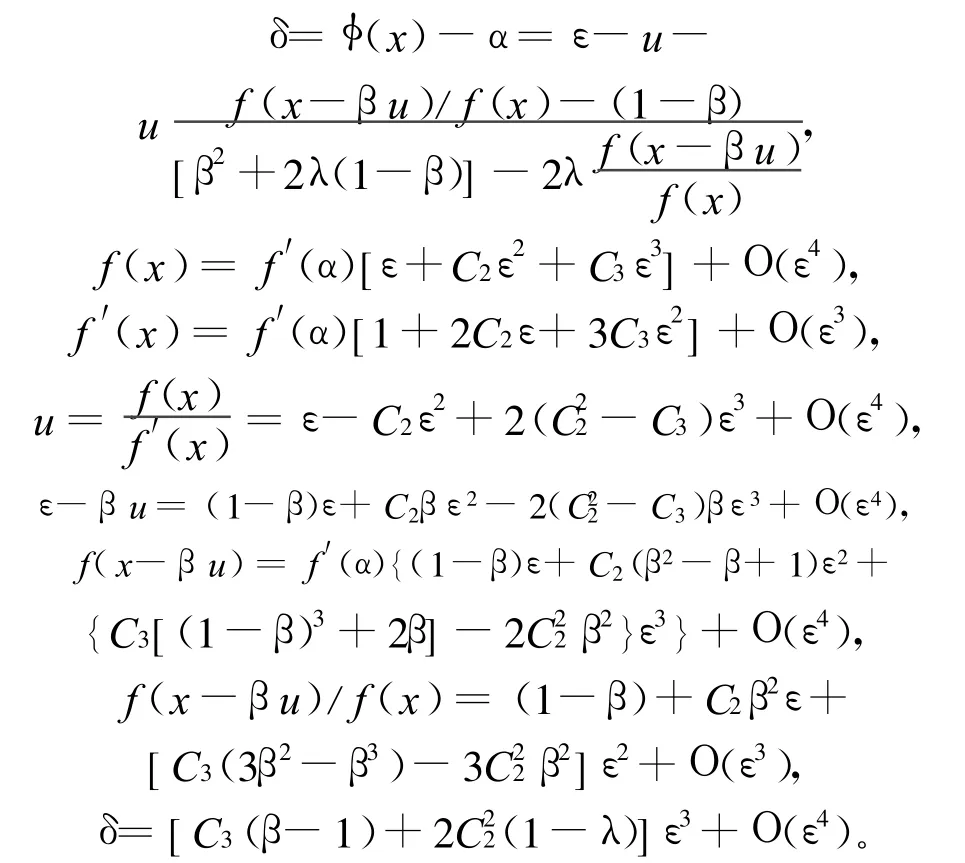
所以当(λ,β)≠(1,1)时,δ=Ο(ε3)。
令xk+1=φ(xk),由定义1可知(1)式是3阶收敛的。
当(λ,β)=(1,1)时,δ=Ο(ε4),令xk+1= φ(xk),同理由定义1可知,(1)式是4阶收敛的。
3 数值分析
本文采用几个不同的函数,不同的初始值分别从迭代次数和rk=|f(xk)|绝对误差方面来比较以上几个方法的优越性。
所有计算都是在M atlab7.0上实现的,迭代过程同时满足|xk+1-xk|<ε和|f(xk+1)|<ε时停止迭代,其中ε=1.0E-30是一个M atlab常数。
例1 已知方程a:f(x)=x2-ex-3x+2,解α=0.257 5。
分别取初始值x0为-1、0、2、20,运用Newton方法(以下简称NM法)、(3)式、(4)式、(7)式、(8)式、(9)式方法进行计算,计算结果见表1所列。

表1 方程a的数值实验结果
例2 已知方程b:f(x)=x3+4 x2-6+ cos(x-1),解α=1。分别取初始值x0为0.5、 0.7、1.8、3.2,运用NM法、(3)式、(4)式、(7)~(9)式方法进行计算,计算结果见表2所列。
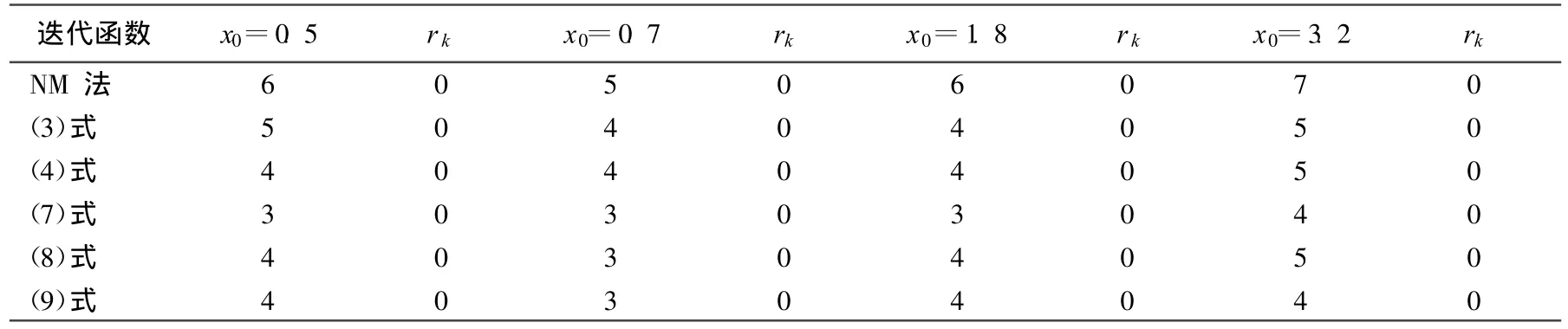
表2 方程b的数值实验结果
例3 已知方程c:f(x)=x cos x+2sin x-1,解α=0.344 6,α=-4.909 5。分别取初始值x0为-0.7、0、0.5、1,运用NM法,(3)式、(4)式、(7)~(9)式方法进行计算,结果见表3所列。

表3 方程c的数值实验结果
以上数值例子表明,本文所给方法的收敛都比较快,且形式简单,便于计算,新方法(9)式较同阶的3阶迭代(3)式、(4)式及(8)式收敛快。
4 结束语
本文给出了一类多参数解非线性方程的迭代格式,证明了该格式至少3阶收敛,且在一定条件下还可以达到4阶收敛,并且只需计算一阶导数,通过适当选取2个参数可以得到很多经典的或已有的迭代格式。数值例子表明了本方法具有收敛快、形式简单,且便于实际应用的优越性,还可以通过选取适当参数得到更多的有利于实际应用的新迭代格式。另外本文方法还可以推广到非线性方程组。
[1] Ham Y,Chun C,Lee SG.Some higher-order modicationsof New ton'sm ethod for solving nonlinear equations[J].Jou rnal of Compu tational and App lied M athematics,2008,222: 477-486.
[2] Bi W,Ren H,W u Q.Three-step iterative method s with eight-order convergence for solving nonlinear equations[J]. Journal of Computational and Applied Mathematics,2009,225:105-112.
[3] Fang L,He G.Some modifications of New ton's method w ith higher-order convergence for solving nonlinear equations[J].Journal of Com putational and Applied Mathematics,2009,228:296-303.
[4] Nedzhibov G H,H asanov V I,Petkov M G.On som e fam ilies ofmulti-point iterativem ethods fo r solving nonlinear equations[J].Num er A lgor,2005,42:127-136.
[5] Kou J,Li Y,W ang X.A modification of New ton method w ith third-order convergence[J].Applied Mathematics and Com putation,2006,181:1106-1111.
[6] Noor M A,Noor K I.Some iterative schemes for nonlinear equations[J].Applied Mathematicsand Compu tation,2006,183:774-779.
[7] Noor M A,W aseem M.Some iterative methods for solving system of nonlinear equations[J].Compu ters and Mathematics w ith Applications,2009,57:101-106.
[8] Noor M A,Shan F A.Variational iteration technique for solving nonlinear equations[J].Jou rnal of Applied Mathematics and Com puting,2009,31:247-254.
[9] 黄象鼎.非线性数值分析的理论与方法[M].武昌:武汉大学出版社,2004:6-64.
[10] 黄云清.数值计算方法[M].北京:科学出版社,2009:223.
