纵横荷载下单桩地基反力法的半解析解

张 磊，龚晓南，俞建霖

(1.浙江大学软弱土与环境土工教育部重点实验室，310058杭州，zh888lei@tom.com; 2.西安建筑科技大学土木工程学院，710055西安)

纵横荷载作用下，不仅其水平荷载将使桩身产生较大的变形和内力，纵向荷载也将因桩身的侧向变形而产生附加弯矩(即P－Δ效应)，而这一附加弯矩又将促使侧向变形进一步增大，尤其当地基土质较差、荷载及地面以上桩长较大时，附加的弯矩和变形更为明显.文献［1－6］分别用实验方法和有限元法进行了研究，并得到很多有益的结论.1977年，日本学者横山幸满［7］给出了纵横向荷载下地基反力系数为常数时长单桩的解析解，并指出应力迭加原理不适用于纵横荷载共同作用下的基桩计算分析.当地基反力系数沿深度线性增加时，赵明华［8］和王哲等［9］给出了幂级数解，李微哲等［10］给出了单、多层地基中考虑桩身初始微倾斜的幂级数解，Han等［11］用变分法分析了考虑桩身横观各向同性时桩的响应.但是，考虑到土的强度随深度的增加而增大、土体变形的非线性、土的屈服以及桩身侧向变形随深度的增加而减小等特点［12］，简单地假定地基反力系数沿深度不变或线性增加并不符合实际情况.另外，考虑到一些粘性土以及岩石在地表处也呈现出一定抗力的情况，地基反力系数在地表处可以不为零.许多学者据此针对水平荷载作用提出了地基反力系数的一般形式［13－15］，并指出地表处土反力和地基反力系数沿深度的分布形式对桩的响应影响很大.然而，目前既考虑P－Δ效应又考虑地基反力系数一般形式的研究未见报道.

本文在研究纵横荷载下基桩变形和内力时引入地基反力系数的一般形式，推导出地面以下桩身的挠曲线微分方程并求得半解析解，结合自由段桩身的幂级数解［9－10］，采用Fortran语言编制了计算程序.通过与幂级数解［9－10］的计算结果进行对比以证明其可靠性，并分析了荷载、地表处土反力和地基反力系数沿深度的分布形式等因素对桩身响应的影响.

1 控制方程及解

1.1 方程的建立

如图1所示，一根桩上半段露出地面，下半段垂直沉入土中，其长度分别为H1和H2.为求解方便，地面以下桩身在C点分成两段，上段(OC段)和下段(CD段)的长度分别为l1和l2，l1+l2= H2.在各段上建立坐标系.桩顶作用水平力Qp、力矩Mp和纵向力Np.假定自由段分布荷载满足线性关系:

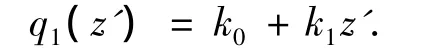
式中:k0和k1为与荷载分布有关的系数.

自由段、OC段和CD段的桩身轴力分别为

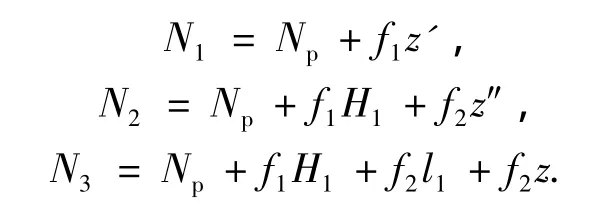
式中:f1和f2分别为自由段和地面以下桩段的轴力增长系数.f1可取为桩身重度与桩横截面积的乘积;数值模拟结果［6］显示地面以下桩身主要侧向变形段上的轴力沿桩身近似成线性分布，即f2可假定为常数，其取值方法参阅文献［9，14］.OC段和CD段地基反力系数的一般形式［13－15］分别为

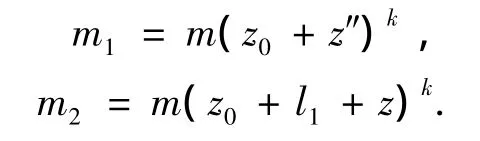
式中:m和k分别为比例系数和指数，均可通过实测或经验确定;z0为地表处的当量深度.当k=0时，可化为文献［7］的情况;当z0=0且k=1时，可化为文献［8－9］的情况.因此文献［7－9］的研究可视为本文的特例.

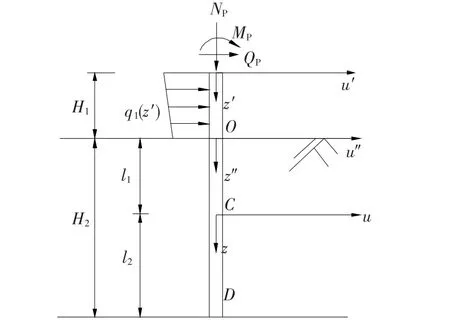
图1 纵横荷载桩示意图

在推导方程时假定:位移以向右为正，转角以向左倾斜为正，弯矩以桩身右侧受压为正，剪力以绕研究对象顺时针转为正.文献［9－10］给出了自由段桩身的挠曲线微分方程为

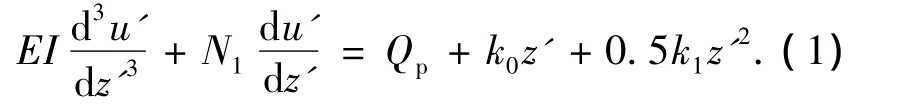
式中:u'为桩身位移.

对于OC段，基于梁在轴、横向荷载作用下的弯曲理论，可得

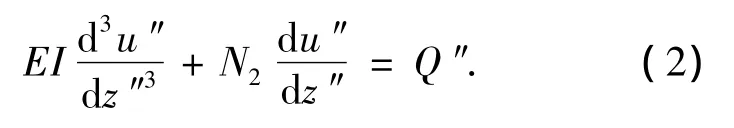
式(2)不能求得解析解或幂级数解，为求得半解析解需进行以下处理，如图2(a)所示，把OC段分成n1个等长的小段.从中任取一段(如第i段)并在其上建立坐标系，如图2(b)所示.假定第i段上桩身轴力和地基反力系数为常数，可分别取为

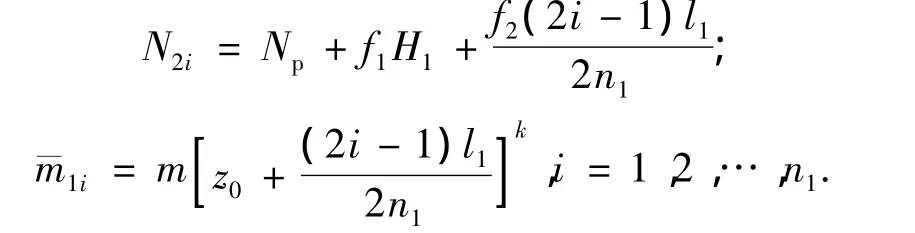
将以上两式代入式(2)并对纵坐标求一次导数，得第i段桩身的挠曲微分线方程为

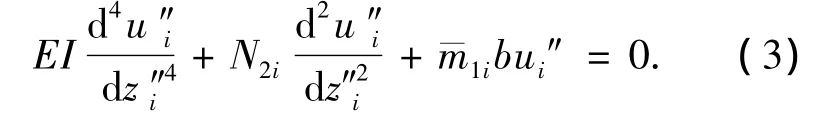
式中:ui″为桩身位移.

同理把CD段分成n2个等长的小段，并在第j段上建立坐标系，如图2(c)所示.第j段桩身的挠曲线微分方程为

式中:uj为桩身位移，N3j=Np+f1H1+f2l1+1，2，…，n2.

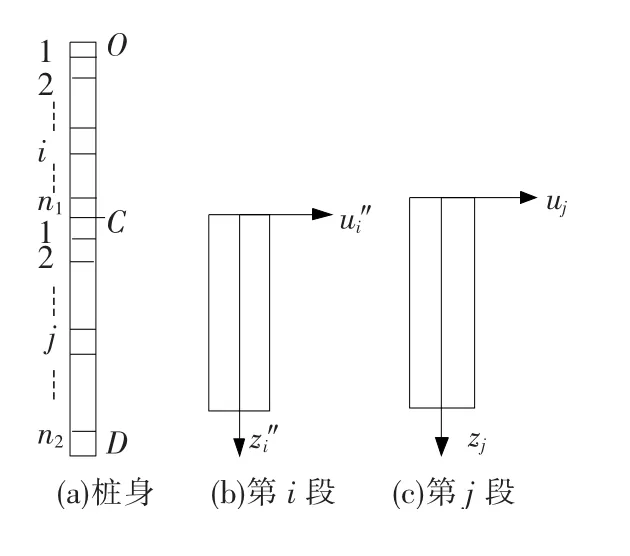
图2 地面以下桩身和桩段示意图

1.2 半解析解

自由段桩身变形和内力的幂级数解为

式中:U'(z')=［u'(z')，φ'(z')，M'(z')，Q'(z')］T，φ'、M'和Q'分别为z'处桩的转角、弯矩和剪切力;U'p=［up，φp，Mp，Qp］T，表示桩顶的变形和内力.矩阵Q和矩阵W具体的表达式已由文献［8－10］给出.

OC段上第i段桩身变形和内力的解为

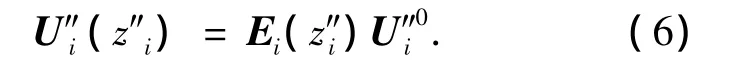
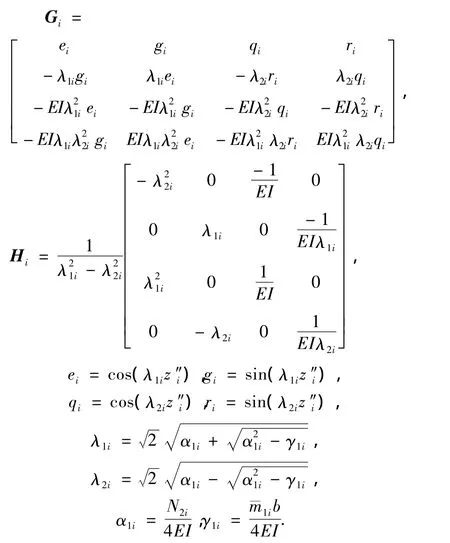
CD段上第j段桩身变形和内力的解为

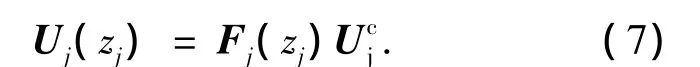
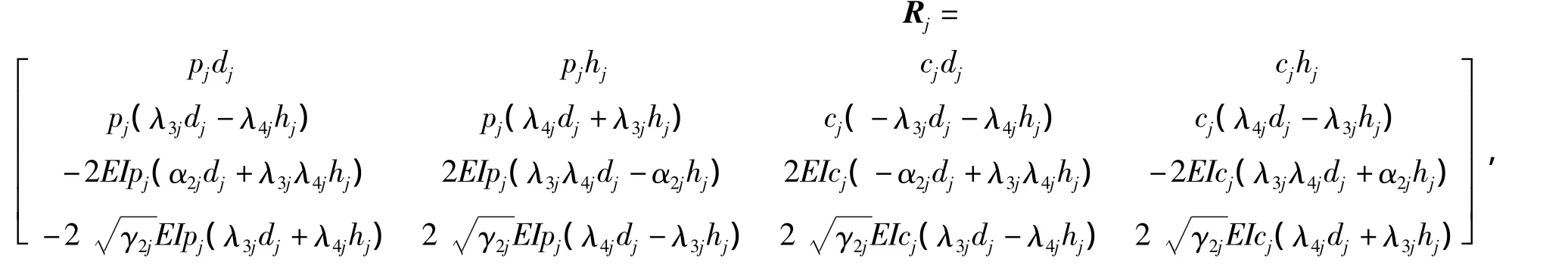
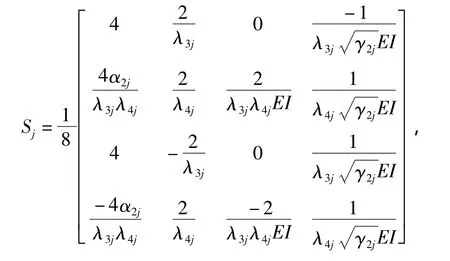
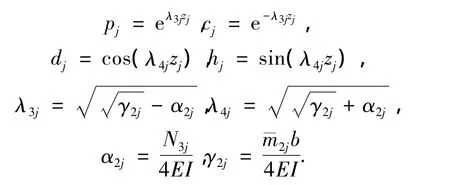
式(5)～(7)即为初参数方程，桩顶未知的边界值可通过桩顶和桩底已知的边界值，由桩的变形和内力在各分界点处的连续性，采用迭代法求得.而对于桩身任意点处的变形和内力，也可根据桩顶的边界值由式(5)～(7)迭代求得.在编程计算时，可适当增加n1和n2的值以获得满意的精度.可以预见:当n1和n2都趋近无穷大时，本文解趋向于精确解.另外，桩的最大位移和最大弯矩是设计纵横荷载桩基础时工程师最为关心的2个参数.桩的最大位移即为已求得的桩顶位移.在求解最大弯矩时需首先采用二分法自桩顶向下求得第1个弯矩微分为零的点，然后比较该点和桩顶的弯矩以得到最大值.

2 算例分析

基于以上解，采用Fortran语言编制了计算程序.为验证解和程序的可靠性，假定z0=0、k=1以与幂级数解［8－10］的计算结果进行比较.本算例中某桥梁桩基自由段长度H1=15 m，地面以下长度H2=30 m，桩的计算宽度b=1.8 m，抗弯刚度EI=9.275×106kN·m2，比例系数 m=6× 103kN/m4，轴力增长系数f1=62.345 kN/m，水平力Qp=300 kN，力矩Mp=200 kN·m，纵向荷载Np=10 000 kN，自由段无分布荷载;桩顶和桩底的边界条件均为自由.另外为方便计算，假定桩身轴力自地面至桩底线性减小到零.本文解及已有解计算出的位移和弯矩沿桩身的分布如图3所示.

由图3可见，2种解计算出的桩身响应吻合的很好，故本文解和程序是可靠的.

利用编制的计算程序，进一步分析水平荷载、纵向荷载以及参数z0和k对桩的最大位移和最大弯矩的影响.图4为桩身响应与纵向荷载关系曲线，图4中有:z0=0.5 m、k=0.8;图5为不同z0值时桩身响应与参数k关系曲线，图5中有:Qp= 400 kN、Mp=100 kN·m、Np=10 MN.桩和土其他的参数均保持不变.

图4表明，当纵向荷载不变时，随着水平力和力矩的增加，最大位移和最大弯矩都将大幅度增大.当水平荷载不变时，随着纵向荷载的增加，最大位移和最大弯矩都增大，且当纵向荷载较小时，增加的幅度不大;随着纵向荷载的增加，最大位移和最大弯矩增加的幅度越来越明显，从图中曲线的后半段可以看出，最大位移和最大弯矩随纵向荷载的增加而急剧增大，此时桩基已经失稳，这与文献［11］的研究成果是一致的.因此当纵向荷载和自由段桩长较大时，P－Δ效应不容忽略.另外还可以看出，当水平力和力矩较大时，纵向荷载的影响也较大，说明水平位移越大，P－Δ效应越明显.图5(a)表明当k＞0且保持不变时，最大位移随z0值的增加而减小，这是由于土抵抗侧向变形的能力随z0值的增加而提高所造成的.图5(b)表明最大弯矩随z0值的增加而减小.如图5所示，最大位移和最大弯矩与参数k的关系受z0值的影响很大.

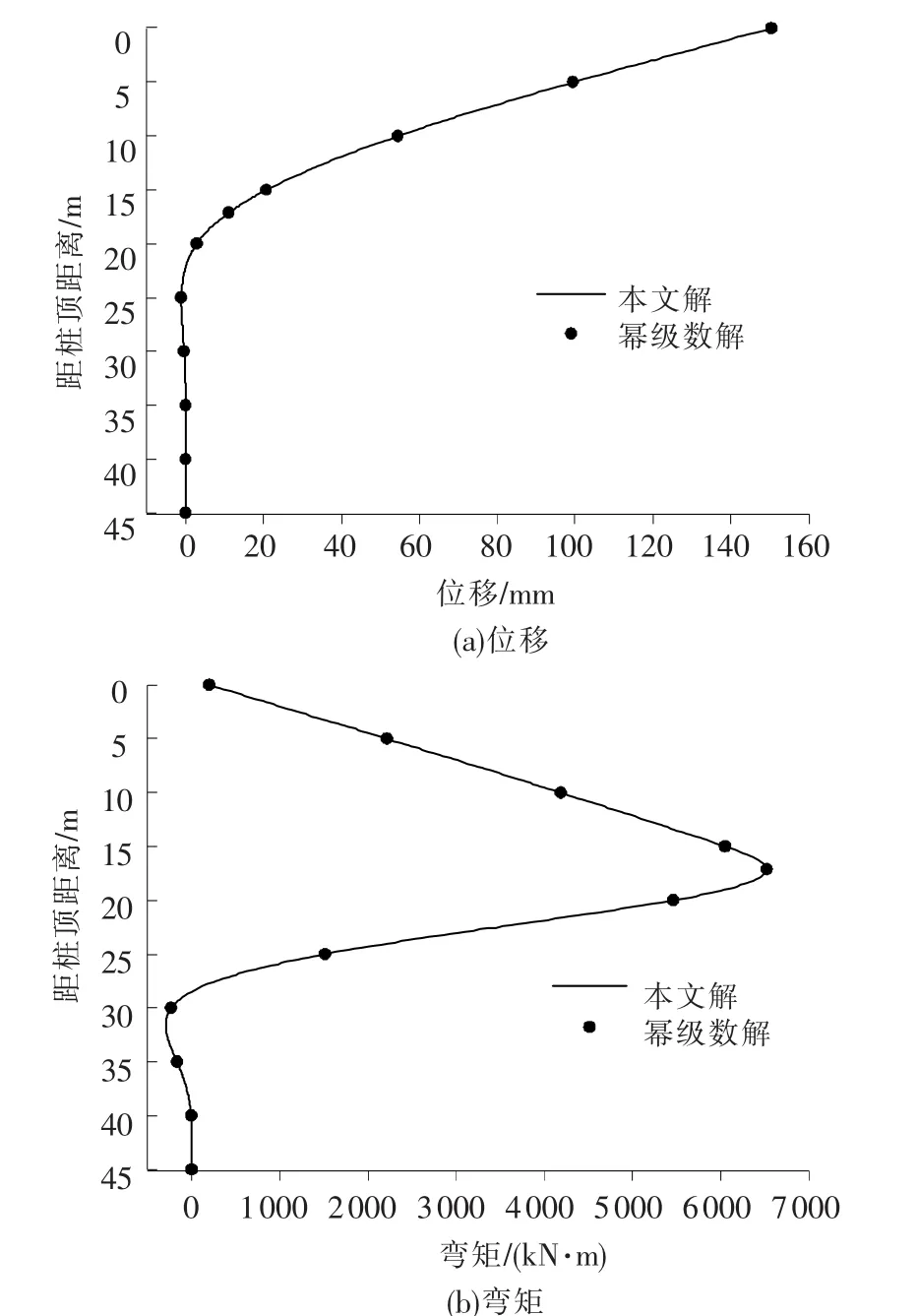
图3 桩身响应分布图

图4 桩身响应与纵向荷载关系曲线

图5 不同z0值时桩身响应与参数k关系曲线

3 结论

1)随着水平荷载的增加，桩的变形和内力均大幅增大.对于无缝梁的桥台桩基，由于伸缩缝的取消，混凝土热胀冷缩引起的水平荷载将大大增加，其影响在设计中需充分考虑.

2)当水平荷载和纵向荷载均较小时，纵向荷载引起的附加变形和附加弯矩很小.但随着水平荷载和纵向荷载的增加，纵向荷载的影响越来越大，甚至会引起桩基失稳.

3)最大位移和最大弯矩随z0值的增加而减小.最大位移和最大弯矩与参数k的关系受z0值的影响很大.

［1］ 赵明华，吴鸣，郭玉荣.轴、横向荷载下桥梁基桩的受力分析及实验研究［J］.中国公路学报，2002，15 (1):50－54.

［2］ 皇甫明，王幼青，张军.纵横向荷载作用下桩的工作性状研究［J］.哈尔滨工业大学学报，2003，35 (6):743－746.

［3］ KIM B T，KIM N K，LEE W J，et al.Experimental load:transfer curves of laterally loaded piles in Nak-Dong River Sand［J］.Journal of Geotechnical and Geoenvironmetal Engineering，ASCE，2004，130(4): 416－425.

［4］ KARTHIGEYAN S，RAMAKRISHNA V V.Influence of vertical load on the lateral response of piles in sand［J］.Computers and Geotechnics，2006，33(2):121－131.

［5］ KARTHIGEYAN S，RAMAKRISHNA V V，RAJAGOPAL K.Numerical investigation of the effect of vertical load on the lateral response of piles［J］.Journal of Geotechnical and Geoenvironmetal Engineering，ASCE，2007，133(5):512－521.

［6］ 郑刚，王丽.成层土中倾斜荷载作用下桩承载力有限元分析［J］.岩土力学，2009，30(3):680－687.

［7］ 横山幸满.桩结构物的计算方法和计算实例［M］.唐业清，吴庆荪，译.北京:中国铁道出版社，1984.

［8］ 赵明华.轴向和横向荷载同时作用下的桩基计算［J］.湖南大学学报，1987，14(2):68－81.

［9］ 王哲，龚晓南.轴向与横向力同时作用下大直径灌注筒桩的受力分析［J］.苏州科技学院学报，2005，18(3):32－36.

［10］ 李微哲，赵明华，单远铭，等.倾斜偏心荷载下基桩内力位移分析［J］.中南公路工程，2005，30 (3):53－57.

［11］ HAN J，FROST J D.Load-deflection response of transversely isotropic piles under lateral loads［J］.International Journal For Numerical and Analytical Methods in Geomechanics，2000，24(5):509－529.

［12］ POULOS H G，DAVIS E H.Pile foundation analysis and design［M］.New York:Wiley，1980.

［13］ 王伯惠，上官兴.中国钻孔灌注桩新发展［M］.北京:人民交通出版社，1999.

［14］ 韩理安.水平承载桩的计算［M］.长沙:中南大学出版社，2004.

［15］ MATLOCK H，REESE L C.Generalized solutions for laterally loaded piles［J］.Journal of the Soil Mechanics and Foundations Division，ASCE，1960，86 (SM5):63－91.