考虑前后信息的车辆跟随自适应控制

任殿波，张 策，张继业

(1.哈尔滨工业大学(威海)汽车工程学院，264209山东威海，rdianbo@tom.com; 2.哈尔滨工业大学(威海)计算机科学与技术学院，264209山东威海; 3.西南交通大学牵引动力国家重点实验室，610031成都)

车辆跟随理论是运用动力学方法，探究在无法超车的单一车道上车辆列队行驶时，后车跟随前车的行驶状态，并且借助于数学模型加以分析阐述的一种理论［1］.关于自动化公路系统的车辆跟随控制研究，已取得很多有价值的研究成果，如文献［2－4］研究了基于PID(Proportional Integral Derivative)控制方法的车辆纵向跟随控制;文献［5］采用了优化方法研究车辆跟随控制;文献［6］采用了模糊控制方法;文献［7－9］采用李雅普诺夫函数方法，对车辆跟随系统的稳定性进行分析，设计车辆跟随滑模控制规律.上述文献在研究中把车辆质量、车辆行驶时受到的地面摩擦力以及空气阻力系数等假定为已知常数，而实际上，这些参数都具有不确定性，如乘客人数的变化以及载货多少会使车辆的质量发生改变，不同的路况往往具有不同的摩擦系数，导致路面对车辆的摩擦阻力也不相同，空气阻力系数也会受到空气密度的变化影响.鉴于此，文献［10－12］基于Lyapunov函数方法，对这些具有不确定性的车辆参数进行在线估计，设计了车辆跟随系统滑模自适应控制规律.上述文献研究中，都是采用“顾前”型的车辆跟随系统模型，即控制系统的设计只考虑前方车辆的状态，而没有考虑后方车辆的状态信息.在自动化公路系统中，车辆列队行驶，车辆间距较小，若车队中某个车辆出现发动机故障，导致该车速度及加速能力低于期望值，容易与后面车辆发生碰撞;而当出现刹车故障时，车辆速度及加速度会大于期望值，容易与前面车辆发生追尾事故.所以，从交通安全和运行效率考虑，对车队中每个车辆的控制系统设计应该同时考虑其前后双方车辆的状态信息.文献［13］建立了考虑前后车速信息的车辆跟驰模型，没有涉及控制系统的设计;文献［14－15］兼顾前后车辆信息，对车辆跟随控制问题进行了研究，但没有考虑车辆参数的不确定性.

本文基于Lyapunov函数方法，考虑车辆前后相邻车辆的位置、速度信息，研究具有不确定参数的“顾前、顾后”型车辆纵向跟随自适应控制，通过计算机仿真对取得的结果进行验证.

1 车辆动力学模型

根据文献［11］，车辆纵向动力学模型可表示为

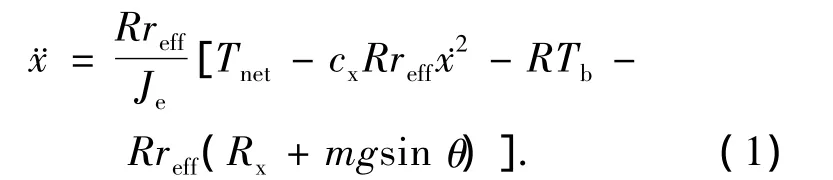
式中:m表示车辆质量;x表示纵向位移;R表示车辆总传动比;reff表示轮胎有效半径;Tnet为发动机净扭矩，Tb表示作用在车轮上的刹车力矩;Rx表示滚动阻力;Je=Ie+It+IwR2+mR2为发动机有效转动惯量，Ie、It和Iw分别表示发动机、传动轴和轮胎的转动惯量;cx表示空气阻力系数，θ为路面俯仰角，g表示重力加速度.

假设不考虑路面俯仰，令M=Je，F=，，分别表示等效的车辆系统模型参数，即等效质量、滚动阻力和空气阻力系数;令 u =Rreff(Tnet－RTb)，表示等效的控制输入，即牵引制动作用力.则方程(1)可简记为

为便于控制系统的设计和分析，本文基于模型(2)进行研究.

2 车辆跟随控制律设计

针对一列车队，如图1所示.假定领头车辆位移x0、速度v0和加速度a0的信息依靠通信系统能传递给其后面的每一个被控制的车辆;第i－1个车辆的位移xi－1、速度vi－1和第i+1个车辆的位移xi+1、速度vi+1信息能传递给第i个车辆.

第i辆车与第i－1辆车之间的车间距误差定义为

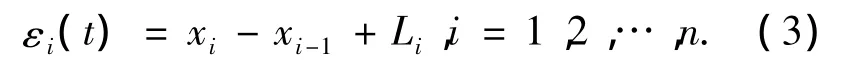
式中:Li表示第i辆车与第i－1辆车之间期望的固定间距，n表示跟随车辆的个数.对车辆跟随进行控制的目的是使εi(t)渐近趋于0.

图1 一个考虑前后信息的车辆编队模型

采用滑模变结构控制方法.定义切换函数

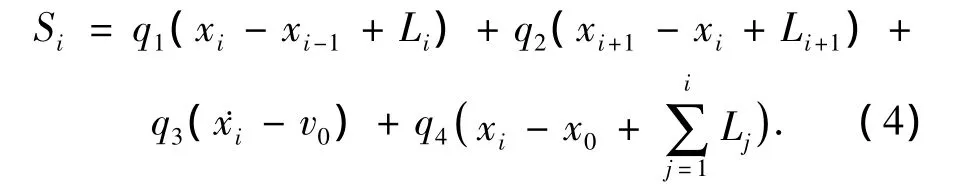
式中q1、q2、q3和q4是待定参数.

假设车辆模型参数Fi、Mi、ci未知，但是慢变的，其估计值分别记为^Fi、^Mi和^ci.为了使˙Si=0，取等效控制

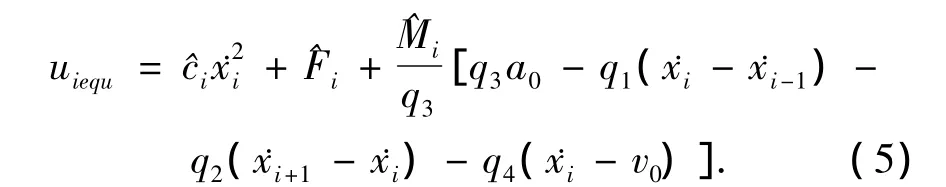
为了使系统状态满足滑动模态的可达条件，取非线性控制

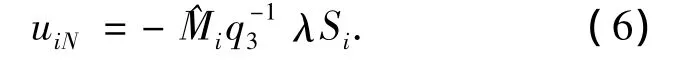
其中λ＞0，是可选的控制参数.控制律采用如下形式

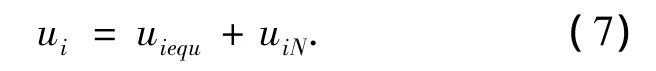
参数自适应律设计为

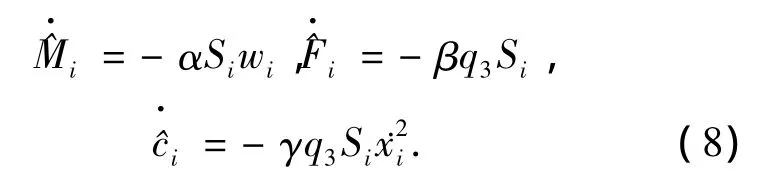
式中:α、β、γ为自适应速率修正因子，均为正;

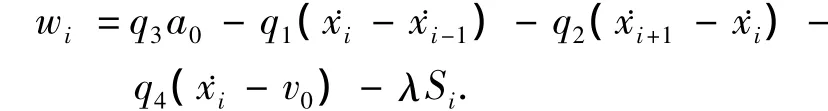
3 车辆跟随系统稳定性分析

首先分析滑模的可达性.根据式(4)，得

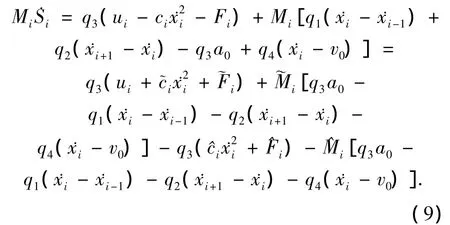
其中

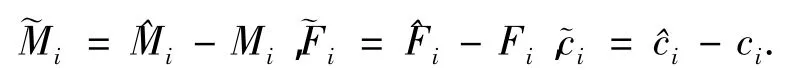
把式(7)代入式(9)，考虑式(5)和(6)，得

取Lyapunov函数

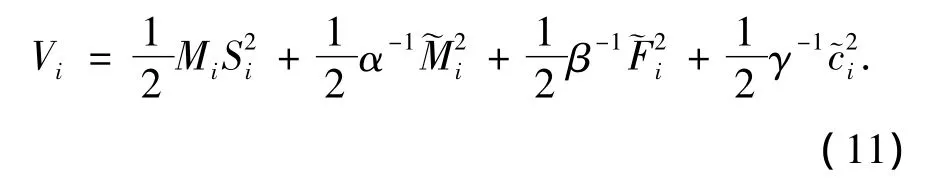
对上式求导，联系式(8)、(10)得

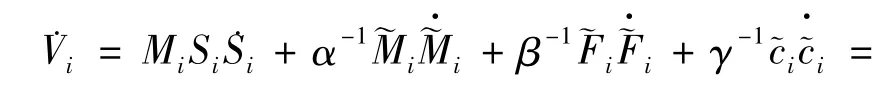
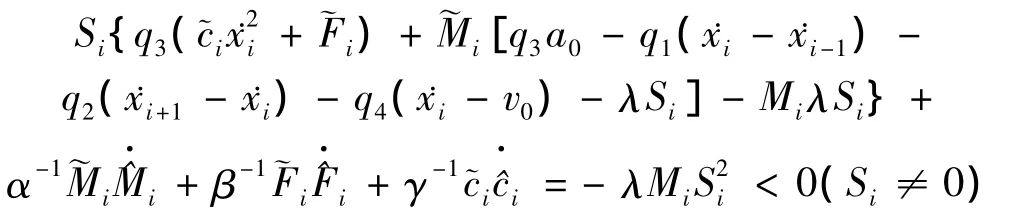
下面考虑系统滑模运动的稳定性.在滑动模态，Si=0，i=1，2，…n.再联系式(3)、(4)，得

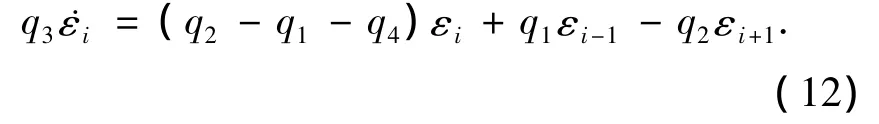
定义ε0=0，εn+1=0，并取

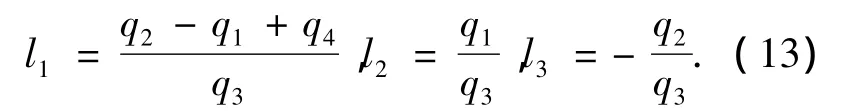
由式(12)得

令ε=［ε1，ε2，…，εn］Τ，式(14)可写为

其中

由线性系统的稳定性理论［17］，假若A为M-矩阵，则式(15)为渐近稳定的.

如果l1、l2、l3满足条件

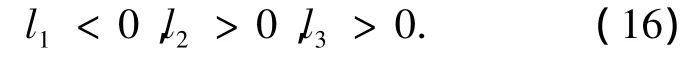
则A的主对角线上元素为正，非主对角线上元素为负;取单位正向量e=［1，1，…，1］Τ，若l1、l2、l3同时满足

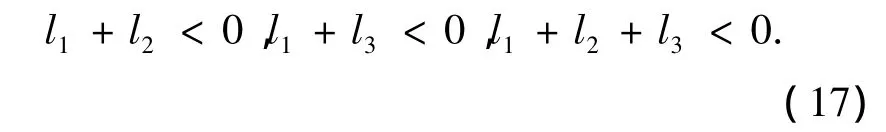
则有Ae＞0，根据M-矩阵知识，可判定A为一非奇异M-矩阵.由式(16)、(17)，再联系式(13)，可得到，只要参数q1、q2、q3和q4满足下面条件

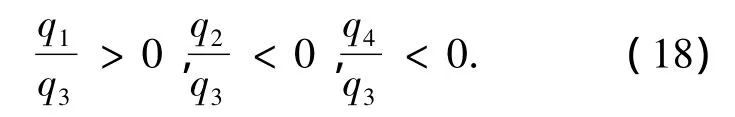
则当t→∞时，εi→0，i=1，2，…，n，即系统滑模运动渐近稳定.

4 仿真实验

假设车辆模型参数Mi、ci、Fi是不知道的，仿真实验中假定Mi=1 000 kg，ci=0.5 N·s2/m2，Fi=200 N，i=1，2，3，4.控制律采用式(7)，其各分量由式(5)、(6)给出;参数自适应规律采用式(8);控制参数及自适应速率修正因子取值见表1.根据式(18)可看出，控制参数q1、q2、q3和q4取值满足车辆跟随系统的稳定性条件.

表1 车辆跟随控制参数

期望车间距Li=12 m，i=1，2，3，4;初始车间距误差ε1=2 m，ε2=1.5 m，ε3=1 m，ε4= 0.5 m;初始速度v0=25 m/s，v1=24.5 m/s，v2= 24 m/s，v3=23.5 m/s，v4=23 m/s;初始位移x0= 100 m，x1=90 m，x2=79.5 m，x3=68.5 m，x4= 57 m;领头车辆加速度历时如下

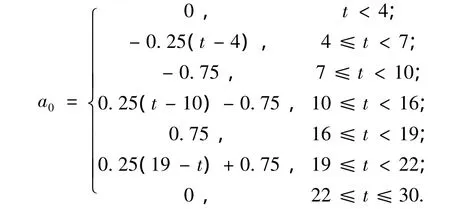
仿真结果见图2～4.图2～3显示，4个跟随车辆的速度能够很快逼近领头车辆的速度，切换函数和车间距误差渐近稳定，且具有快的收敛速度，其中虚线表示的是领头车辆，实线表示跟随车辆.图4反映了对未知参数的估计情况，图中虚线表示参数的真实值，实线表示对参数的估计值.参数估计值的调节受跟踪误差的收敛性影响，跟踪误差趋于0时，参数估计值趋于稳定值，系统的渐近稳定性并不需要模型参数的估计值收敛到其真实值［16］，可以看出，对M的估计，4个跟随车辆质量的估计值并没有收敛到实际值1 000 kg.

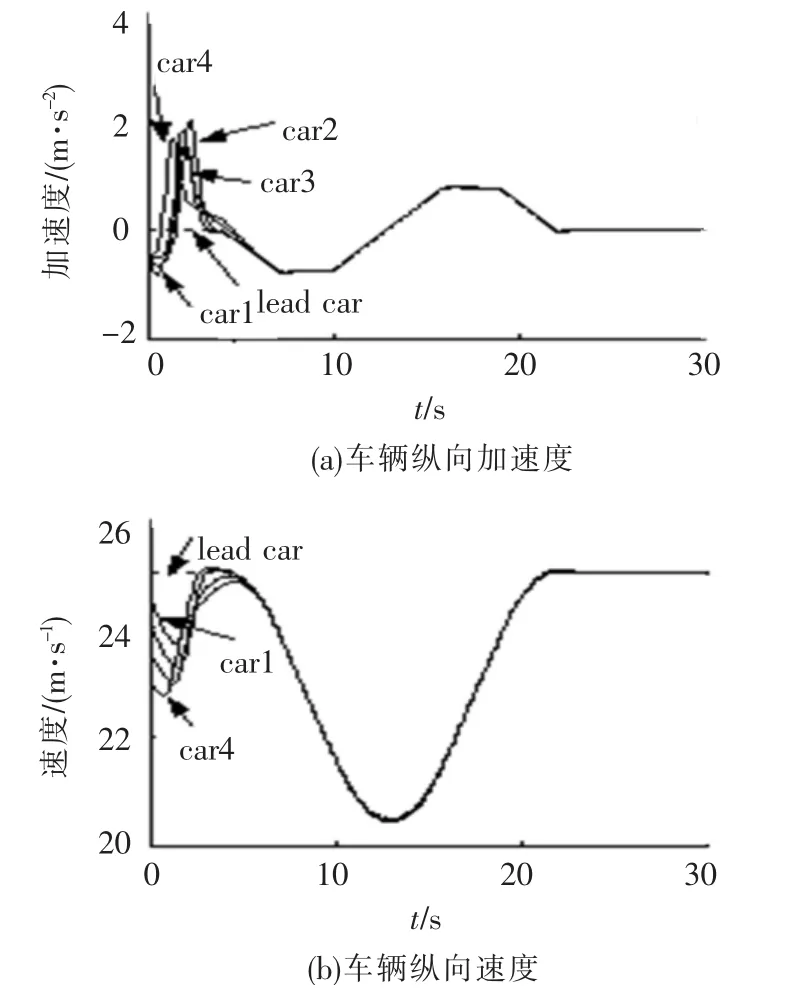
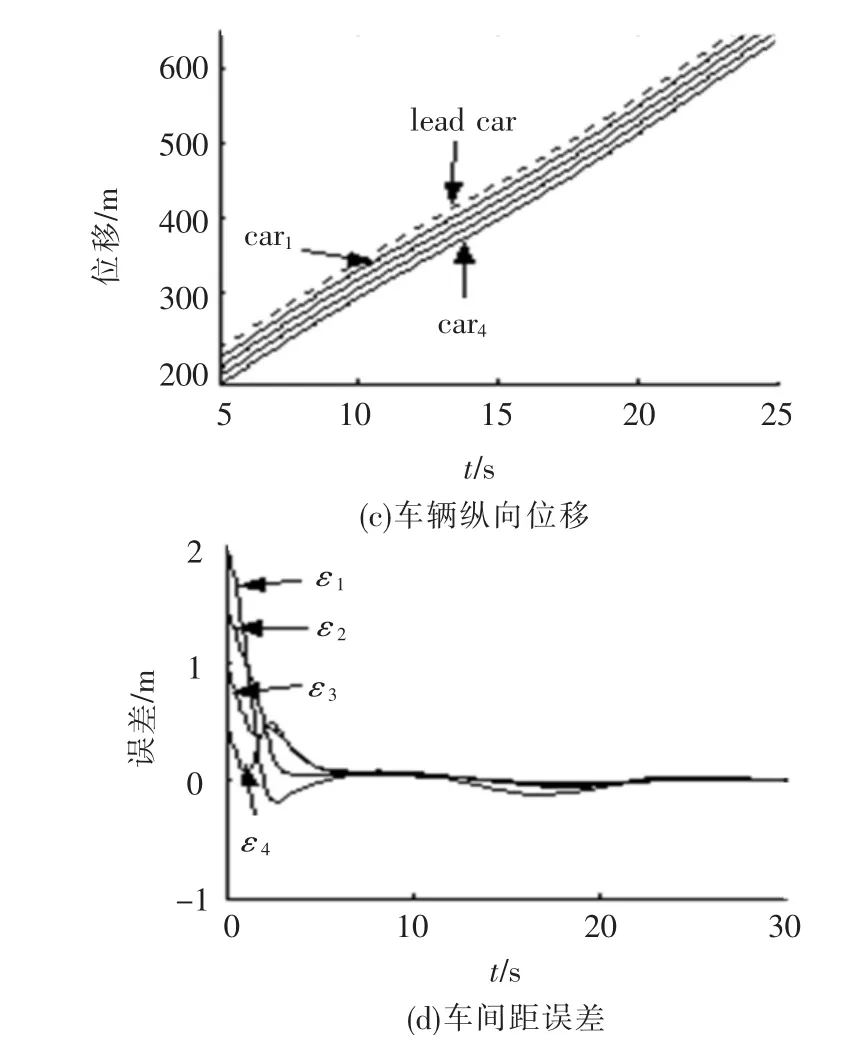
图2 车辆状态及车间距误差

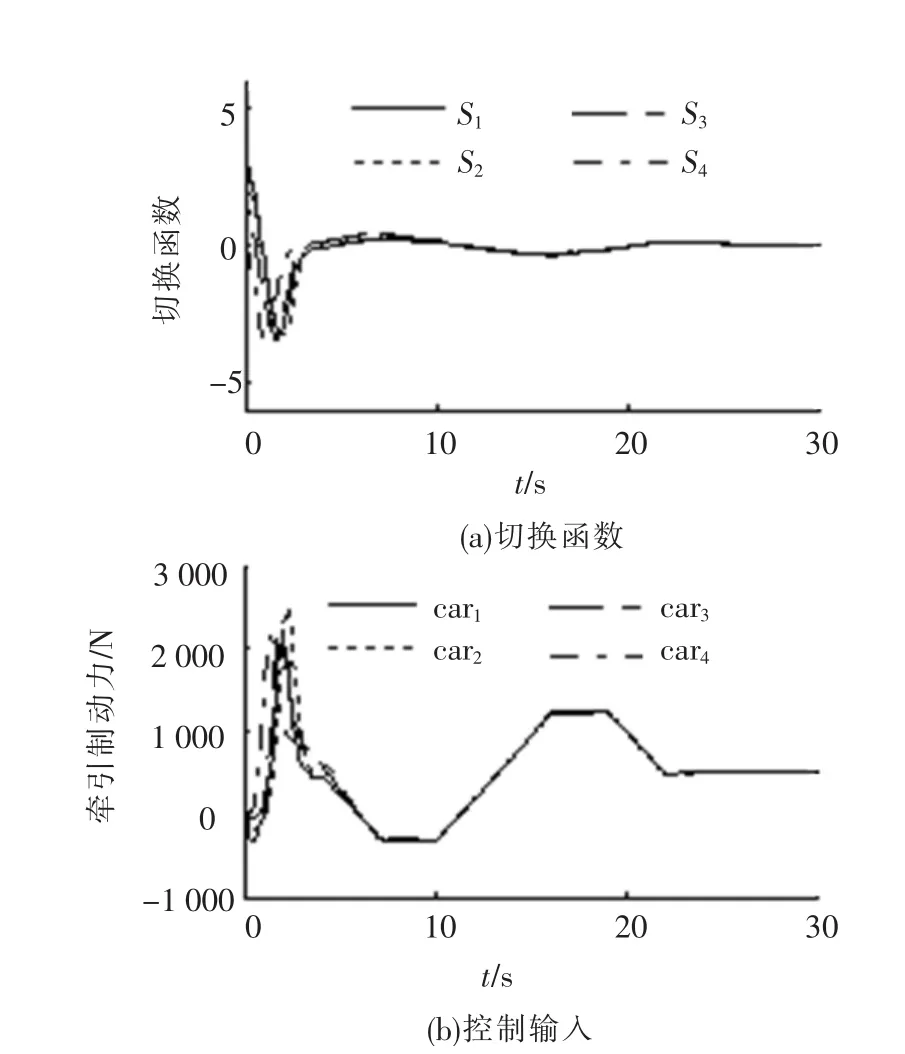
图3 切换函数与控制输入

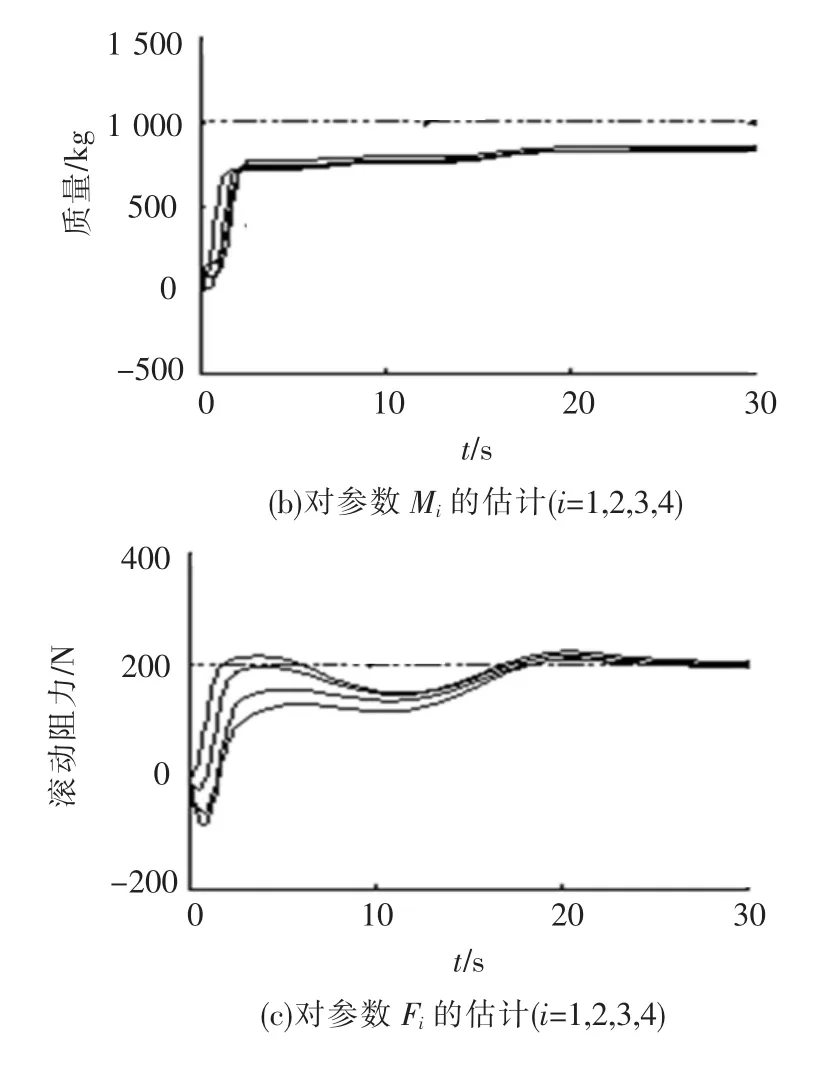
图4 参数估计

5 结论

1)对考虑前后车辆信息的自动化公路系统车辆跟随控制问题进行研究，设计了具有不确定参数的车辆跟随变结构控制规律和不确定参数自适应规律.

2)基于Lyapunov稳定性理论，应用M-矩阵知识，对滑模的可达性和滑模运动的稳定性进行了分析，得到了系统渐近稳定的充分条件.在控制参数满足该条件的情况下，设计的控制规律和参数估计式能保证滑模渐近可达，车间距误差渐近稳定.

3)通过一个5车辆编队，对文中结果进行了验证.由于控制参数有较大的收敛域，实践上便于应用.

［1］ NAGEL K.Particle hopping models and traffic flow theory［J］.Physical Review E，1996，53(5):4655－4672

［2］ ZHANG J，IOANNOU P A.Longitudinal control of heavy trucks in mixed traffic:environmental and fuel economy considerations［J］.IEEE Transactions on Intelligent Transportation Systems，2006，7(1): 92－104.

［3］ DRUZHININA M，MOKLEGAARD L，STEFANOPOULOU A G.Parameter estimation and supervisory techniques for robust longitudinal control of heavy vehicles［R］.PATH Research Report，UCB-ITS-PRR-2003-15.Berkeley:University of California，2003.

［4］ FUJIOKA T，ASO M，KIMURA T.Longitudinal vehicle following control for autonomous driving［C］//Proceedings of International Symposium on Advanced Vehicle Control.Aachen，Germany:JSAE，1996:1293－1304.

［5］ SAINTE-MARIE J，MAMMAR S，NOUVELIERE L，et al.Sub-optimal longitudinal control of road vehicles with capacity and safety considerations［J］.ASME Journal of Dynamic Systems，Measurement，and Control.2004，126(1):26－35.

［6］ ARACIL J，HEREDIA G，OLLERO A.Global stability analysis of fuzzy path tracking using frequency Response［J］.Engineering Applications of Artificial Intelligence，2000，13(2):109－119.

［7］ SWAROOP D，HEDRICK J K.String stability of interconnected systems［J］.IEEE Transactions on Automatic Control，1996，41(3):349－357.

［8］ ZHANG Jiye，SUDA Y，IWASA T，et al.Vector Lyapunov function approach to longitudinal control of vehicles in a platoon［J］.JSME International Journal (Series C)，2004，47(2):653－658.

［9］ 任殿波，张继业.基于Lyapunov函数方法的时滞车辆纵向跟随控制［J］.控制与决策，2007，22(8): 918－926.

［10］ SWAROOP D，HEDRICK J K，CHOI S B.Direct adaptive longitudinal control of vehicle platoons［J］.IEEE Transactions on Vehicular Technology，2001，50(1):150－161.

［11］ RAJAMANI R.Vehicle dynamics and control［M］.New York:Springer，2006.

［12］ RAN Dianbo，ZHANG Jiye.Adaptive algorithm to vehicle following control in intelligent transportation system［C］//Proceedings of the International Symposium on Information Processing.Moscow，Russia: IEEE CS，2008:46－50.

［13］ 熊烈强，王富，李杰.考虑前后车速度关系的车辆跟驰模型［J］.华中科技大学学报:自然科学版，2005，33(9):87－90.

［14］ COOK P A.Stable control of vehicle convoys for safety and comfort［J］.IEEE Transactions on Automatic Control，2007，52(3):526－531.

［15］ COOK P A，SUDIN S.Convoy dynamic with bi－directional flow of control information［C］//Proceedings of the IFAC Symposium on Control Transportation Systems.Tokyo，Japan:IFAC，2003:433－438.

［16］ SLOTINE J E，LI W.Applied nonlinear control［M］.Beijing:China Machine Press，2004.

［17］ 舒仲周，张继业，曹登庆.运动稳定性［M］.北京:中国铁道出版社，2001.