无喷管助推器组合药柱研究①

2011-03-13鲍福廷胡海峰

固体火箭技术 2011年3期

丁林，鲍福廷，胡海峰，蔡强，陈超

(西北工业大学航天学院，西安 710072)

0 引言

无喷管助推器结构简单，无零部件抛落危险，可靠性高。在20世纪70年代初，研究人员就以简化固体火箭发动机的结构和降低成本为目的，对其进行了初步研究［1－2］。此后，欧美各国将无喷管固体火箭发动机作为整体式固冲发动机的助推器，对其内弹道性能计算、试验和理论性能分析以及流场多维效应等方面开展了大量研究［3－5］。无喷管助推器与一般固体火箭发动机相比，燃气的膨胀、加速不充分，工作过程后期压强低，药柱燃烧不完全，燃烧效率偏低，导致有效比冲下降。为提高比冲，研究人员进行了很多改进，如选用高燃速、低压强指数的推进剂［6］和双燃速组合药柱［7－8］。其中，无喷管助推器组合药柱内弹道性能影响因素的复杂性，如推进剂燃烧规律、药柱变形、混合燃气以及2种燃速药柱交界面处燃面变化、低燃速药柱冲刷等，使得传统的半经验设计方法和内弹道计算模型已不再适合，而详细复杂的多维流场分析也不能满足工程研制时快速有效的需求。

本文主要采用一维非定常变截面有加质内弹道模型，对双燃速药柱无喷管助推器进行数值计算，研究组合药柱形式对无喷管助推器性能的影响，为固冲发动机无喷管助推器设计、理论性能预示和优化提供参考。

1 组合药柱方案

无喷管助推器的内弹道特点是工作初期的压强峰值较高，压强-时间曲线呈单调下降趋势，且下降速度很快，工作末期的压强约为压强峰值的25% ～40%。由于药柱通道壅塞截面不断扩大，但燃面也不断增加，这样使得推力曲线基本保持平直或上升趋势。燃烧室压强的单调下降使壳体强度的利用率下降，平均压强较低，也制约着助推器和冲压发动机性能的提高。为此，研究人员提出了组合药柱方案。

1.1 组合药柱方案

本文研究的组合药柱方案主要有:2种燃速推进剂分段药柱;2种燃速推进剂分层药柱，而分层药柱又分为恒定厚度层和可变厚度层，如图1所示。

(1)分段药柱方案

分段药柱方案的前段是高燃速推进剂，后段是低燃速推进剂，此方案的目的在于减小药柱通道壅塞截面扩大的速率，即尽量保持药柱尾部的“喷管”造型，从而使压强曲线的下降幅度一定程度地减小，同时增大平均扩张比。

(2)分层药柱方案

分层药柱方案的内层为低燃速推进剂，外层为高燃速推进剂，由于压强峰值一般都出现在工作初期，且与推进剂燃速密切相关，此方案的目的即为降低初始压强，且在药柱通道烧蚀过程中，保持了通道剖面的光滑度，以不致使药柱内出现大的局部断裂应力或剪切力。对于恒定厚度层分层药柱方案，其制造工艺相对简单，但工作过程中会出现2次压强峰值现象，可能会引发助推器工作不稳定等问题;而可变厚度层分层药柱方案能有效避免此问题，但制造工艺相对复杂。

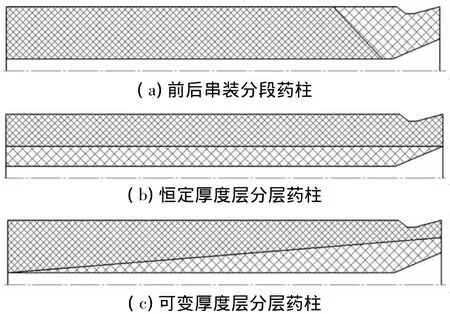
图1 组合药柱示意图Fig.1 Schematics of the combined grains

1.2 算例

在上述药柱方案的基础上，形成4个算例，如表1所示。算例c0采用单燃速推进剂，用来作为比较基准。算例c1、c2和c3使用双燃速推进剂，其高燃速推进剂燃速特性与算例c0相同，c1、c2和c3之间的低燃速推进剂燃速特性相同。

4个算例的药柱基本结构参数参照文献［7］公布的尺寸:药柱外径φ238 mm，内孔直径φ60 mm，药柱总长1 210 mm(含冲压喷管)，药柱扩张段长度110 mm，药柱扩张锥半角22°。

表1 算例说明Table 1 Summary of the examples

2 内弹道计算模型

2.1 基本假设

对无喷管助推器内弹道计算所涉及的流动描述，现在一般采用纯气相或考虑固相粒子作用的两相流模型，前者是后者的简化子集。本文采用一维非定常变截面有加质的流动模型，为便于处理，做以下假设:

(1)流动是一维绝热的，流动参数是时间t和坐标x的函数，燃烧和加质过程瞬间完成，燃烧产物的加质方向与x轴方向垂直;

(2)燃烧在燃面附近薄层内完成，主要通道内燃烧产物为纯气相且成分冻结;

(3)2种燃速的推进剂燃烧产物热力性质相同，仅是燃速不同;

(4)忽略药柱变形;

(5)忽略燃气的体积力和辐射热;

(6)燃气服从理想气体状态方程。

2.2 控制方程

对于一维非定常变截面有加质的流动，其守恒型的控制方程如下:

其中:

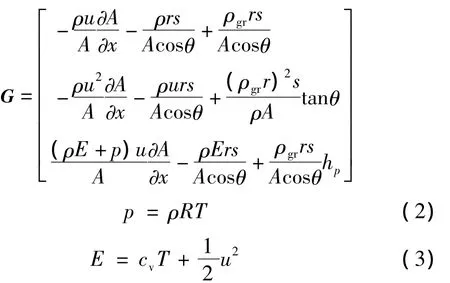
式中 ρgr为推进剂密度;r为推进剂线性燃速;s为燃面周长;A为通道截面积;hP为推进剂比焓;θ为当地燃面与x轴线方向的夹角。

2.3 控制方程数值解法

为了使网格节点合理分布，对x坐标作如下变换:

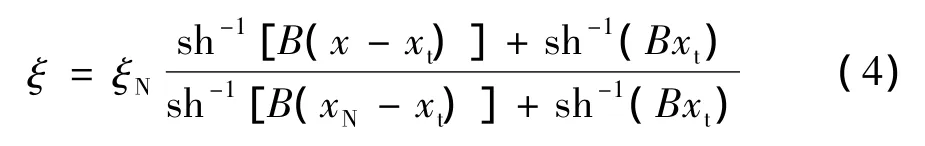
式中 xt为圆柱内孔末端坐标;xN为通道出口处坐标;B为拉伸因子。

控制方程(1)坐标变换后可写为

其中:

差分格式采用MacCormack预估-校正两步显格式。为了使数值计算稳定，引入人工粘性项。

预估步:

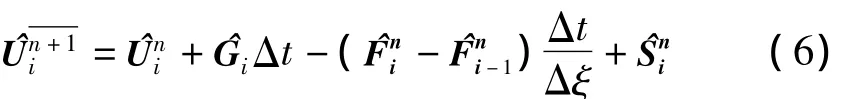
校正步:

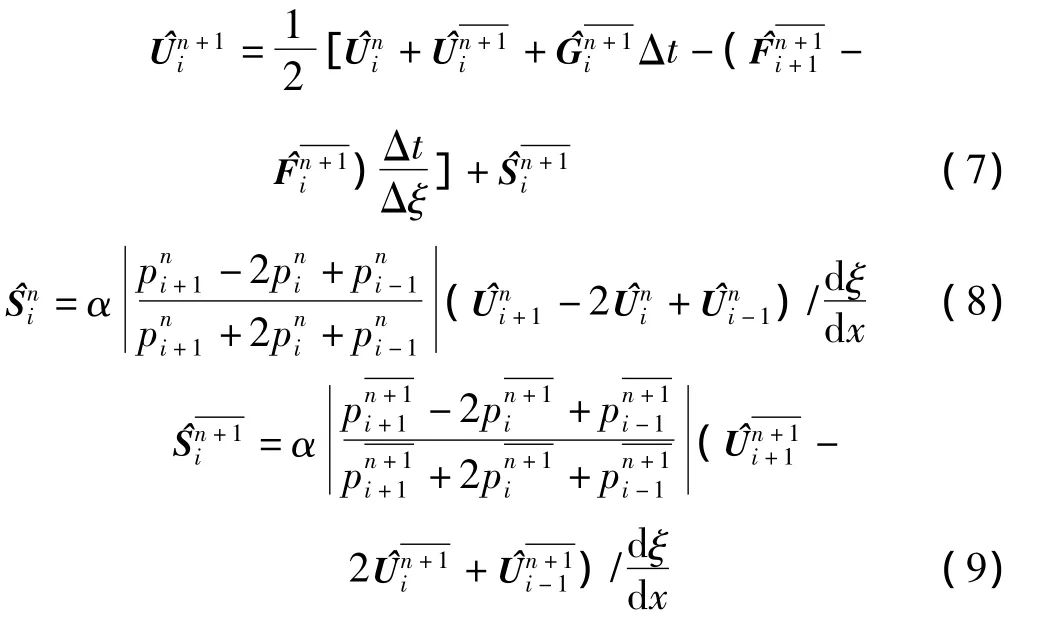
时间步长Δt的选取受CFL条件限制，取

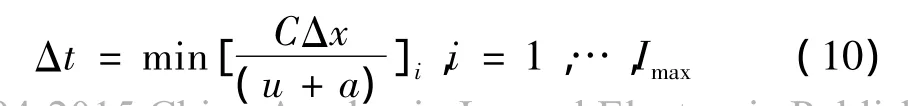
式中 Imax是总结点数;C为CFL数，0＜C＜1，开始计算时，C应取得小一些，然后逐步加大。

2.4 边值条件

(1)求解的初始条件

计算初始时刻(t=0)，整个通道内气体处于静止状态，气体压强为环境压强，气体温度为推进剂初温，气体速度为0。

(2)求解的边界条件

在上游边界处(x=0)燃气流速为0，温度为燃气总温，密度由外推得到，压强根据式(2)确定。下游边界处(x=L)，当气流速度为亚音速时，给定出口压强为环境压强，流速和密度由外插确定;当气流速度为超音速时，全部参数由外插确定。

2.5 燃速模型

方程求解过程中，对于无喷管助推器工作过程中推进剂燃速的处理，采用基础燃速加侵蚀燃烧燃速形式，推进剂总的燃速公式:

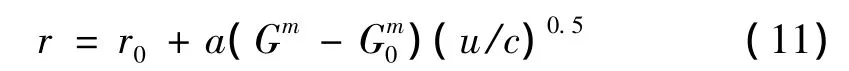
基本燃速公式r0采用维耶里经验公式:

若考虑初温的影响:

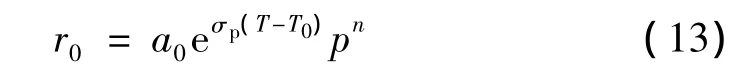
式中 G为燃气质量流率;σp为推进剂燃速温度敏感系数。

这样，影响燃速的侵蚀燃烧、推进剂初温也都纳入模型，提高了模型精度。

关于计算过程中组合药柱2种燃速的处理，为简化模型，已假设2种燃速推进剂产生的燃气热力性质相同，不考虑交界面处可能产生的再生燃面或复杂燃面。初始时，给出高低燃速药柱的分界面参数，计算过程，中判断已燃肉厚是否已超过低燃速药柱肉厚，如未超过，则采用低燃速公式;若超过，则选用高燃速公式。计算公式为

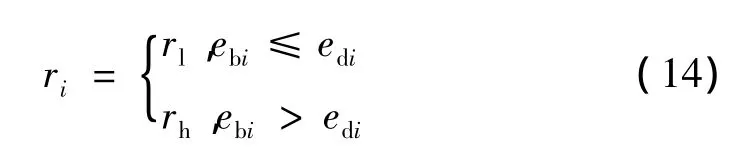
式中 ri表示i点处燃速;rh和rl分别为高、低燃速公式;ebi为i点处已燃药柱肉厚;edi为初始时i点处低燃速药柱肉厚，即分界面参数。

2.6 模型验证

为了验证采用该内弹道计算模型编制的计算程序，对文献［9］中的试验助推器进行数值模拟，将得到的理论预示结果与地面试验数据对比，如图2所示。从图2可看出，理论预示曲线与试验曲线吻合得较好。对曲线进行数据处理，得到的助推器性能参数理论预示值与试验值误差在5%以内。

此外，对文献［8］中的双燃速试验助推器进行数值模拟，将结果与试验数据对比，如表2所示。从表2可知，数值模拟与地面试验的误差最大为2.6%，这表明本文对组合药柱2种燃速的处理是合适的。

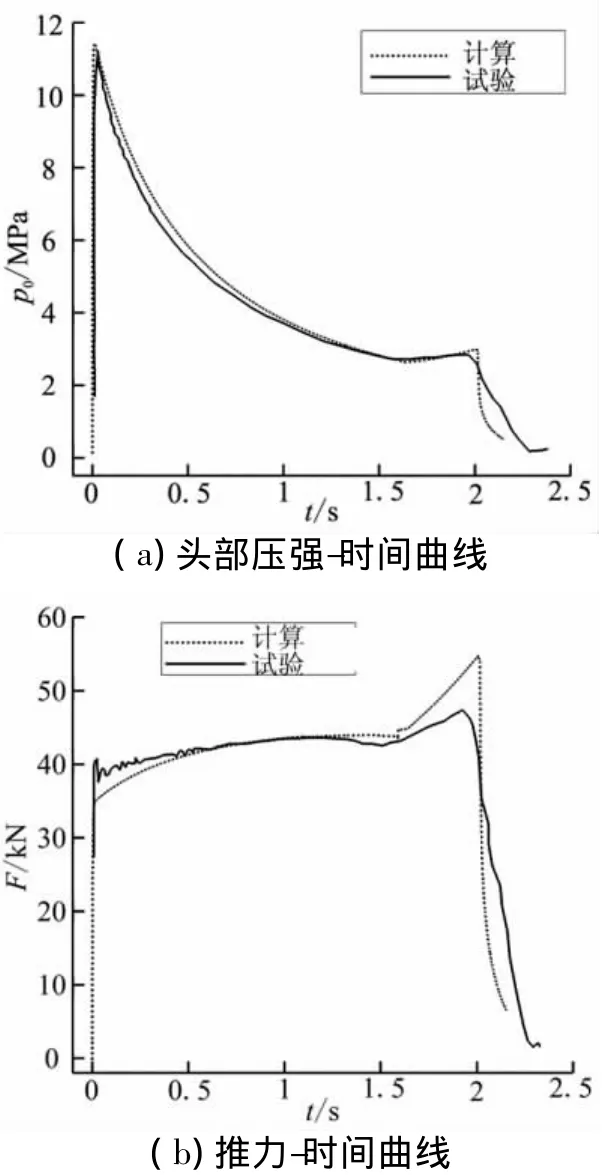
图2 内弹道理论预示曲线与试验曲线比较Fig.2 Comparison of calculated and experimental curves

表2 双燃速药柱助推器数值计算与试验数据对比Table 2 Comparison of calculated and experimental results of dual burning rate grain nozzleless booster

经过上述验证，说明本文编制的计算程序对于实际工况描述基本正确，计算精度能满足工程研制的需要。

3 计算结果分析

各算例的头部压强-时间曲线和推力-时间曲线如图3和4所示。从图3可看出，算例c0压强下降得很快，1.7 s内就从13.9 MPa 降到2.6 MPa;算例 c1初期(0 ～0.3 s)压强下降也很快，随后(0.3 ～1.8 s)下降速度明显变缓，维持在5 MPa以上，这是一个相当高的压强水平;算例c2的压强-时间曲线存在显著的2个峰值，初期压强峰值较低(6.3 MPa)，后期1.4 s时刻处再次出现1个更低的压强峰(5 MPa)，这是内层低燃速药柱燃尽、外层高燃速药柱开始燃烧所造成的结果;算例c3压强曲线较平缓，在前期1.8 s内压强维持在5 MPa左右，这与其他算例不同。

从图4可发现，算例c0推力单调上升，曲线较平缓，但在1.7 s时刻后，推力上升速度突然加快，推力曲线变陡。这是因为冲压喷管露出来后，喉径大小不再随药柱燃烧而扩大;算例c1的推力上升得很快，且当药柱烧尽(1.8 s)时，推力达到最大值;算例c2呈现两级推力，0～1.2 s为第一级推力工作时间，1.2～3.0 s为第二级推力工作时间，每一级推力曲线都较平缓，但两级推力相差很大(50 kN)，出现明显的台阶现象;算例c3的推力先上升后下降，初始推力较低，仅有20 kN，在1.8 s时刻处达到峰值，并在1.8 ～2.1s内维持在峰值85 kN左右，随后逐渐降低。

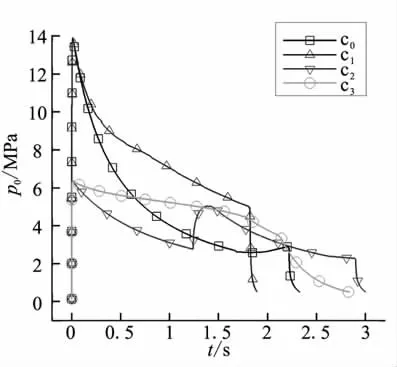
图3 压强-时间曲线Fig.3 Pressure-time curves

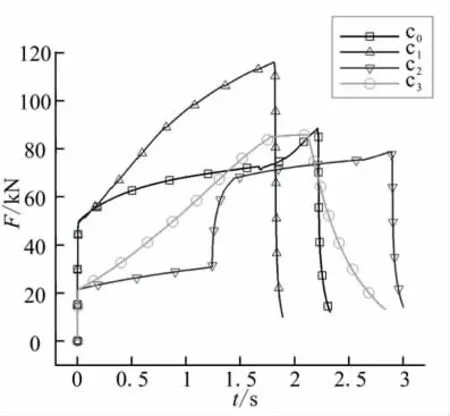
图4 推力-时间曲线Fig.4 Thrust-time curves

各算例计算所得性能参数如表3所示。算例c0与c1的最大压强接近，而c2和c3是c0最大压强的45.4%和45.9%。这表明双燃速分层药柱能明显降低无喷管助推器的初始压强峰值。算例c1与c0相比，其比冲提高了6.7%，即126.52 m/s，其平均压强高达压强峰值的53.8%，也明显高于c0的34.6%。这表明双燃速分段药柱能减缓药柱通道壅塞截面的扩大速度，即药柱尾部的“喷管”作用明显，能有效提高比冲和平均工作压强，增加了壳体强度利用率;c2的比冲比c0提高1.1%，而c3的比冲是c0的97.5%，但其工作压强较低。对壳体强度要求降低，因此，可减小壳体壁厚，减轻助推补燃室质量，从而提高固冲发动机综合性能。

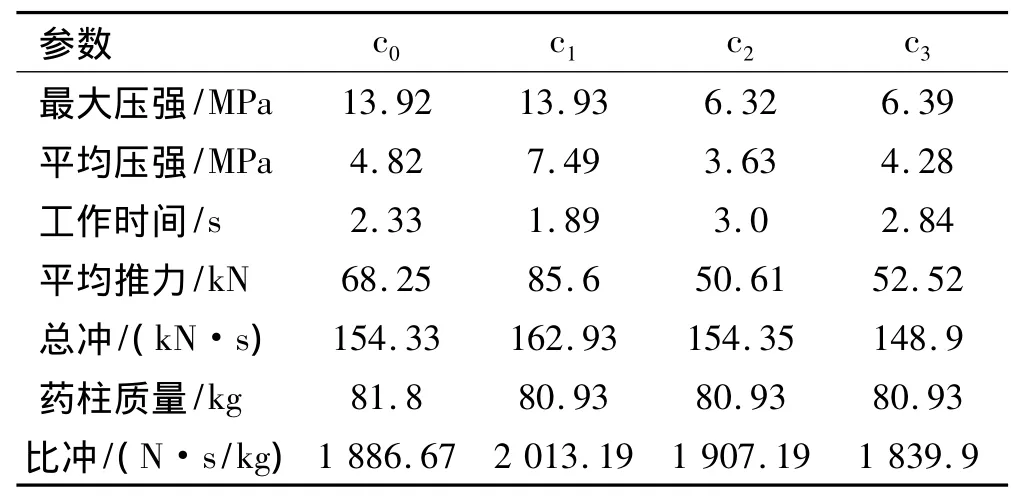
表3 算例性能参数Table 3 Performance parameters of the examples

4 结论

(1)比较了3种不同形式的无喷管助推器组合药柱的工作特点:分段药柱的推力一直上升，曲线较陡，其最大值比单燃速药柱高出31.1%，工作时间缩短18.9%，压强下降速度变缓;分层药柱的初始推力较低，仅为单燃速药柱的43.4%，工作时间增加21.9%以上。其中，恒定厚度层式药柱内弹道曲线有明显的台阶现象。

(2)与单燃速药柱相比，双燃速分段组合药柱比冲可提高6.7%，平均压强提高55.4%;双燃速分层组合药柱比冲可提高1.1%，压强峰值降低54.6%。说明组合药柱能提高比冲，增加壳体强度的利用率。

(3)所编制的内弹道计算程序对无喷管助推器组合药柱性能进行数值模拟，与参考文献中试验结果的误差在5%以内，能满足工程研究需要，可为固冲发动机无喷管助推器设计、理论性能预示和优化提供一种快速计算的手段。

(4)通过优化2种燃速推进剂的选择和组合药柱的结构参数，如增大高低燃速之比、降低压强指数及改变高低燃速药柱的组合位置，无喷管助推器的性能还可进一步改善。

［1］Price E W.One-dimensional，steady flow with mass addition and the effect of combustion chamber flow on rocket thrust［J］.Jet Propulsion，1955，25(2).

［2］Procinsky I M，Catherine A McHale.Nozzleless boosters for integral-rocket-ramjet missile systems［R］.AIAA 80-1277.

［3］Coats D E，Dang L，Nickerson G R.Interior ballistics calculations for nozzleless solid propellant rocket motors［R］.AIAA 82-1199.

［4］Nahon S.Nozzleless solid propellant rocket motors experimental and theoretical investigations［R］.AIAA 84-1312.

［5］King M K.Consideration of two-dimensional flow effects on nozzleless rocket performance［R］，AIAA 84-1313.

［6］曹任刚.无喷管固体火箭发动机内弹道计算［J］.航空兵器，2006(1):57-60.

［7］汪志清.无喷管固体发动机药柱技术研究［J］.推进技术，1994，15(3):56-61.

［8］霍东兴，陈林泉，严利民.双燃速串药柱柱无喷管助推器性能分析［J］.航空兵器，2008(4):40-43.

［9］陈林泉，毛根旺，霍东兴，等.无喷管助推器非定常动边界内流场数值模拟［J］.固体火箭技术，2008，31(5):453-460.