残差自回归模型在中国人口出生率预测中的应用

山东大学公共卫生学院(250012) 刘晓冬 姜宝法

时间序列是将某一指标在不同时间上的数值按时间先后顺序排列而成的数列〔1〕。时序分析中对非平稳时间序列的处理有两种方法:(1)确定性分析方法，假定序列的变化不是变化莫测的，而是可以用一条趋势线来加以刻画的，即序列的趋势是时间t的确定函数，常用的方法有线性模型、指数模型等〔2〕。该方法只能提取确定性信息，没有利用随机性信息。(2)随机性分析方法，ARIMA模型是典型代表，通过差分方法提取确定性信息，能提高非平稳序列的拟合精度，但难以对模型进行直观解释。残差自回归(error auto-regressive Model)模型〔3〕综合了上述两种方法的优点，成为非平稳时间序列分析的重要方法。本文利用该模型对中国人口出生率进行拟合并预测，旨在探讨该模型在卫生领域中的适用性。

资料与方法

1．资料来源

本研究所利用的数据是中国1975～2008年的人口出生率数据，来源于中国卫生部《2009中国卫生统计年鉴》〔4〕，数据真实可靠。

2．残差自回归模型介绍

一般回归分析要求残差之间相互独立，而时间序列经一般回归分析后的残差通常具有自相关性，这违背了一般回归分析残差独立的前提，且大大降低了拟合精度〔3〕。而残差自回归模型的构造思想是:首先通过确定性因素分解方法提取序列中的确定性信息，然后再检验残差序列的的自相关性。构建的确定性回归模型如下:

其中，a是常数项，b为线性回归系数，{εt}为残差序列。

由于受模型本身的精度和随机因素的影响，因素分解方法对确定性信息的提取可能不充分，需对残差序列{εt}进行自相关性检验。如果检验结果显示残差序列自相关性不显著，说明模型(1)对信息的提取比较充分，分析可以结束;如果检验结果显示残差序列自相关性显著，说明模型(1)对信息的提取不充分，需要继续对残差序列拟合自回归模型。本研究所采用的残差自相关性检验方法是Durbin-Waston检验(简称DW检验)。下面以残差1阶自相关性检验为例介绍DW检验的原理。

即 DW≌2(1-ρ)，因为 －1≤ρ≤1，所以 0≤DW≤4。当0＜ρ≤1时，序列正相关;当－1＜ρ≤0时，序列负相关。

若检验结果显示残差序列无自相关性，提示确定性回归模型对信息的提取较充分，分析可到此为止;若检验结果显示残差序列存在自相关性，须进一步提取相关信息，可用自回归模型对残差序列进一步拟合，构造的模型{vt}如下:

将(1)式和(5)式结合，就构成了残差自回归模型:

其中，φp是残差自回归模型系数，{at}是均数为0、方差为σ2的正态独立白噪声序列。

3．本研究使用 SAS9．1．3 软件包中的 SAS/ETS〔5〕模块进行分析。平稳性检验采用时序图法，纯随机性检验采用LB统计量。

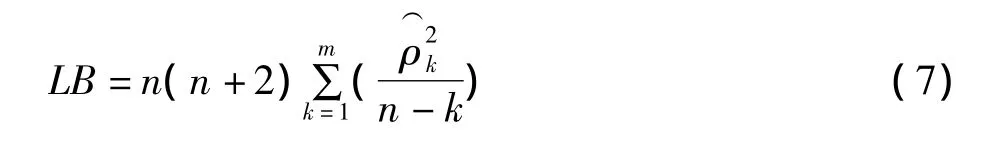
若LB统计量的P值＜0.05，则可以认为该序列是一非纯随机序列或非白噪声序列。

模型应用

首先对该时间序列进行平稳性检验和纯随机性检验，若该时间序列为非平稳和非纯随机序列，然后使用Error Auto-regressive模型对该数据进行拟合。平稳性检验结果见图1。

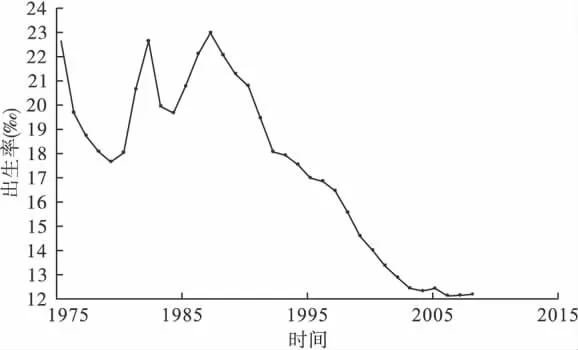
图1 中国1975～2008年人口出生率时序图

时序图显示，该序列有一个明显的下降趋势，并伴有一定的波动，是一个非平稳时间序列。

纯随机性检验结果:

延迟6阶的LB统计量为107.73(P＜0.0001)，说明该序列是一非白噪声序列。

经以上检验，该序列是一非平稳非白噪声序列，可以用error auto-regressive模型进行拟合。

确定性模型为:

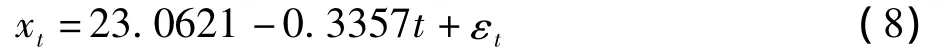
对残差序列{εt}进行自相关性检验，得DW=0.293 0(P＜0.000 1)，表明该残差序列具有自相关性，下面对该残差序列用自回归模型进行拟合。用逐步回归法筛选显著的自相关因子，并使用ML法进行参数估计。3-5阶的自相关项无统计学意义，故从模型中消除，只保留显著的1阶和2阶自相关项。结果见表1。

表1 残差序列自回归模型拟合结果

拟合的残差序列自回归模型为:

下面将确定性模型拟合过程和残差序列自回归模型拟合过程同时进行，将所有参数联合求解，得拟合的最终模型参数估计结果见表2。

拟合的最终模型为:

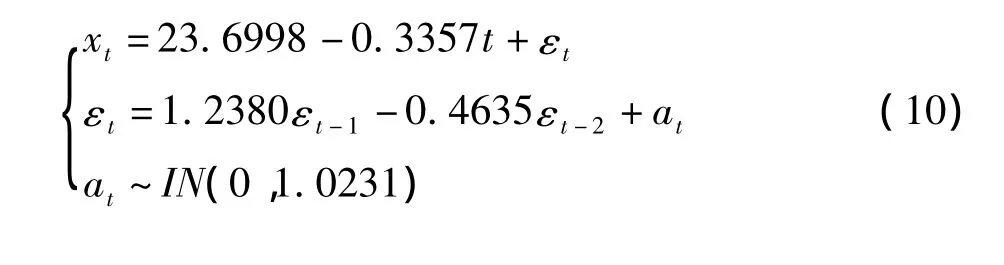
最终模型拟合的R2=0．9322，高于确定性模型;MSE=1.0231，AIC=102.75，SBC=108.85，明显小于确定性模型，说明最终模型的拟合效果优于确定性模型。对残差序列{at}进行自相关性检验，DW=1.8767，P=0.2909，不能拒绝H0，可以认为残差序列{at}自相关性无意义，不需要继续进行分析。

表2 最终拟合模型输出结果

图2 最终模型拟合效果图

图2为模型拟合效果图。图2中，黑点表示的是原始序列值，虚线为确定性模型拟合线，实线为最终模型拟合曲线。可以看出，最终模型的拟合效果明显好于确定性模型。应用该模型预测中国2009～2011年人口出生率分别为12.05‰、11.86‰、11.60‰。

讨 论

随着社会的发展和计算机技术的进步，时间序列分析技术的应用越来越广泛，在卫生领域中的应用日益深入〔5，6〕。国内外医学界也正在寻求借助时序分析技术解决医学问题的途径。残差自回归模型是一种拟合非平稳时间序列的方法，它既能提取序列的确定性信息，又能提取其随机性信息，不仅提高了模型的拟合精度，还使结果符合实际，变得更易解释，兼具了时间序列确定性分析和随机性分析的优点。当一个时间序列具有明显的确定性趋势或季节效应时，可考虑应用此模型。在医学、农业、工业、气象、经济等领域中的诸多现象都具有时间序列的特征，残差自回归模型的应用也日趋广泛。尤其在生物医学领域，如我国妇幼卫生监测网监测的出生缺陷率、孕产妇死亡率以及多种传染病的发病率等都具有非平稳时间序列的特征，可利用残差自回归模型对其进行拟合和预测。

本文采用的是中国1975～2008年人口出生率时间序列数据，经平稳性和纯随机性检验，该数据为非平稳非白噪声序列，呈明显的下降趋势，并伴有一定的波动。若仅用一般线性回归进行拟合，残差序列会存在自相关性，对序列信息的提取不充分。本研究在对数据拟合了确定性模型后，对残差序列进行自相关性检验，发现残差序列有自相关性，遂继续拟合残差自回归模型，得到最终模型。由结果部分可知，该模型的拟合效果明显好于确定性模型。需要说明的是，表1估计的参数值数值不一致，这是因为确定性模型和残差自回归模型是分开求解的，忽略了残差序列{εt}和序列

最终模型其实是一个组合模型，由确定性模型和残差自回归模型组成，但通常把该组合模型称为残差自回归模型。需要注意的是，残差自回归模型同时对时间序列的确定信息和随机信息进行拟合，所以时间序列样本点不能过少，一般不能少于30个。当序列较短时，只能进行确定性时间序列分析〔7〕。残差自回归模型的计算虽然复杂，但借助计算机技术可方便快捷地实现这一过程，如应用 SAS/ETS模块中的 AUTOREG过程，通过自行编程可以灵活实现不同领域时间序列的残差自回归模型拟合。因此，残差自回归模型的应用有着良好的发展前景。

1．王振龙主编．时间序列分析．北京:中国统计出版社，2000:2．

2．王春平，王志峰，单杰，等．随机时间序列分析法在传染病预测中的应用．中国医院统计，2006，13(3):229-232．

3．王燕．应用时间序列分析．北京:中国人民大学出版社，2005:167-178．

4．中华人民共和国卫生部《2009中国卫生统计年鉴》．http://www．moh．gov．cn/publicfiles/business/htmlfiles/zwgkzt/ptjnj/year2009/t-8．htm．

5．高慧璇等编译．SAS系统·SAS/ETS软件使用手册．北京:中国统计出版社，1998，116-153．

5．吴家兵，叶临湘，尤尔科．时间序列模型在传染病发病率预测中的应用．中国卫生统计，2006，23(6):482-485．

6．华来庆，熊林平，孟虹，等．AR-EGARCH模型在疾病指数时间序列建模中的应用研究．中国卫生统计，2006，23(3):276．

7．陶庄，金水高．时间序列分析简明攻略．中国卫生统计，2003，20(3):151-153．