非线性混合效应模型和广义线性模型拟合随机效应logistic回归的应用比较

杨志雄 袁岱菁

在临床药物试验中药物疗效的评价经常遇到二分类资料，即反应变量有两个水平如有效、无效;成功、失败等。二分类变量服从二项分布，可采用logistic回归模型。

运用logistic回归模型对分类资料进行分析，能给实际研究带来很多便利。与多元线性回归相比，logistic回归具有许多独特的优点，如对正态性和方差齐性不做要求，系数的可解释性等。正是这些优点，使得logistic回归成为广受欢迎的分析工具。但是需要指出的是，logistic回归模型只能处理具有独立性的资料，即观测数据应来自完全独立的随机样本。

在实际研究中经常会碰到样本之间具有相互关系的观测数据(correlated data)。比如，临床研究中的交叉设计试验，在不同试验条件下对同一对象的重复观测。

由于重复测量数据间存在自相关性，因而增加了传统统计方法对该类数据分析的难度。适合此类数据的统计分析方法就必须考虑数据之间的这种相关性。这些方法大多是传统logistic回归的扩展，大致可归为两类:边际模型(marginal model)和随机效应模型(random effect model)〔1〕。

对于交叉设计试验中，在不同试验条件下对同一对象(受试者)的重复观测的数据，考虑到同一受试者在不同处理，不同阶段下测量数据之间的相关关系是由受试者的内在特性引起的，而这种特性在不同受试者之间是不相同的，且无法实际观测到，所以适用随机效应的logistic回归模型。

我们既可以用非线性混合效应模型，也可以用广义线性模型来拟合随机效应的logistic回归。SAS提供了不同的过程步来实现非线性混合效应模型和广义线性模型，分别是PROC NLMIXED，PROC GLMMIX。

下面就用一个实例来介绍并比较用两种模型拟合交叉设计试验下随机效应logistic回归。

模型与原理

1.非线性混合效应模型

非线性混合效应模型亦称为多水平非线性模型、非线性随机效应模型或非线性分层模型。它可以直接拟合非线性模型。不仅能识别和估计个体间和个体内的变异，而且也考虑了解释变量与反应变量参数间的非线性关系，允许固定效应和随机效应进入模型的非线性部分，相对于线性模型的正态假定，非线性模型对资料的分布无特殊要求，资料可以是正态，也可以是二项分布、Poisson分布等。

非线性混合效应模型可作如下表述:

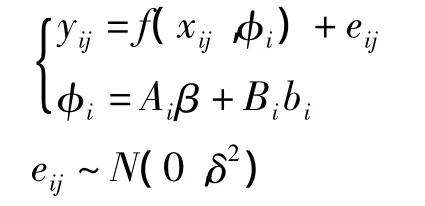
其中，yij为第i个体第j次测量预测值，或经过某种单调联系函数(1ink function)转换的值;f(·)为非线性函数，如果其为线性，则退化为线性的混合效应模型;xij为P维解释变量向量;eij为独立正态分布随机误差向量;β为P维固定效应参数;bi为随机效应因子;Ai、Bi为已知的设计矩阵。其参数估计可以通过伪数据步(pseudo—data step)和线性混合效应步(1inear mixed effects step)两步之间的迭代完成，可分别使用Gauss—Newton迭代法和 EM 算法解决〔2〕。

2.广义线性混合效应模型

广义线性混合模型(gneralized linear mixed models，GLMMs)是广义线性模型(generalized linear models，fGLMs)与线性混合效应模型(1inear mixed model)的扩展．通过在模型中纳入随机效应来解释数据间的相关，过度离散(overdispersion)、异质性(heterogeneity)等问题。

其模型表述为:

ui为随机效应项，反应变量Yij的条件分布的期望;

条件均数uij(考虑了随机效应)通过联结函数g(．)与条件线性预测值ηij联结;

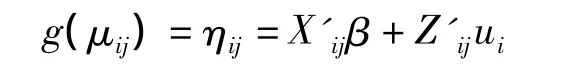
上式为广义线性混合模型的一般式，Yij:第i类的第 j个观测的反应变量，i=1，…，m，j=l，…ni。考虑随机效应ui的条件下独立，服从指数分布族，可以是二项分布、Poisson分布、Gamma分布等。

Xij为解释变量，β为固定效应参数矢量，ui随机效应，服从均数为0，方差协方差矩阵为γ的多变量正态分布，ui解释了由于不可测因子引起的类间的异质性和同一类内观测到的相关，不同类间的ui是相互独立的，Zij为与随机效应相关的解释变量。设计矩阵分固定效应X与随机效应Z两部分。分析的数据不同可以选择不同的联结函数g(·)，可以拟合含随机效应的 logistic回归等多种模型〔3〕。

应用实例

某公司开发一种新药用于治疗泌尿系统疾病。以安慰剂为对照，将所有患者随机分为两组，一组患者先服用新药A，再服用对照药B;另一组患者顺序相反，即先服用对照药B，再服用新药A，每个阶段用药2周，期间洗脱期1周，进行2×2交叉设计试验，共纳入病例30例。主要结果指标疗效为每阶段结束后，病人填写PRTI量表。该量表由三个问题组成:包括病人对治疗的总的满意度，是否优先选择研究中使用的治疗和是否愿意再使用研究药物。每一个问题上的得分是1～5分。其中1分为最满意，5分为最不满意。为了便于分析，按照PRTI量表评分的情况将疗效划分的2个等级，即有效和无效，分别赋值为1，0。当评分为1分和2分时，认为有效，赋值为1。当评分为3分，4分和5分时，认为无效，赋值为0。这样三个问题中每个问题都会产生一个二分类变量。因篇幅有限，本例中的结果仅针对于对第一个问题即病人对治疗的总的满意度的分析。

统计分析方法以病人对治疗的总的满意度即药物是否有效为应变量，处理(treat)、阶段(period)、受试者(subject)为解释变量，其中处理和阶段纳入为固定效应，受试者(subject)作为随机效应，建立非线性混合效应模型。其模型基本形式为:

随机效应 ui～Normal(0，δ2)。

所有分析过程在SAS软件中完成。

用非线性混合效应模型PROC NLMIXED分析数据，所建立的模型在经过10次迭代后收敛。采用常用的Dual quasi-Newton最优化技术与Adaptive Gaussian积分方法，－2Loglikelihood=77.8，参数估计结果表1。

表1 非线性混合效应模型参数估计表

本表列出了4个参数和它们的最大似然估计值，标准误，以及统计推断。beta0是截距，表示处理和阶段效应为0时的对数优势(log-odds)。接下来几行分别是处理(beta1)，阶段(beta2)，随机效应(s2u)的估计。每个系数都可以通过取幂来转换成优势比。检验水准α=0.05处理效应，阶段效应和受试者效应均无统计学意义，如果某项效应有统计学意义，解释为，通过取幂可以计算在控制了有关混杂因素后该效应的优势比。

用广义线性混合效应模型PROC GLMMIX分析数据，所建立的模型在经过8次迭代后收敛。采用常用的Newton-Raphson with Ridging最优化技术，－2 Res Log Pseudo-Likelihood=259.04，参数估计结果见表2和表3。

表2 随机效应估计表

表3为模型中固定效应的解决方案。结果显示处理效应和阶段效应研究药物组和安慰剂组相比两组间比较均无统计学意义差异。

表3 固定效应估计表

GLIMMX参数估计的解释与NLMIXED类似。同时有注意到变量在GLIMMX中显示了变量名，协方差参数1．0051与NLMIXED表中s2u等价。可以看出，虽然用NLMIXED过程步产生的参数估计值与GLIMMX结果不同，但是两个方法得出的结论是一致的。

讨 论

医学研究中常会遇到非线性重复观测的二项分布数据分析的问题。对于二项分布数据的分析，常常采用logistic回归模型，但是标准logistic回归模型要求数据满足独立性的要求。重复观测的数据不独立。如本例中交叉设计的临床试验数据，数据间存在自相关性且随机误差至少分为两个层次，即个体间误差和个体内重复测量误差。分析此类数据不仅需要考虑不同层次的误差，而且也需要考虑参数间的非线性关系〔4〕。

非线性混合效应模型考虑了不同层次的误差和参数间的非线性关系。允许固定效应和随机效应进入模型的非线性部分，可以拟合具有随机效应的logistic回归模型，在临床研究领域有着越来越广泛的应用。

而广义线性混合模型中随机效应也可以以非线性形式进入模型，反应变量既可是连续变量，也可是分类变量，常用来处理相关数据、纵向观测数据、过度离散的数据。随机效应变量之间既可以独立也可以相关。可以根据需要拟合logistic随机效应模型，在医学领域中同样应用广泛。

实例中，采用SAS软件中的PROC NLMIXED和PROC GLMMIX过程来分析数据。比较NLMIXED和GLIMMIX，二者有几处重要的不同，在实际应用中选择哪个应仔细考虑。

首先是二者使用的估计方法不同。二者都利用了参数估计的方法。NLMIXED利用高斯积分来积分近似，而GLIMMIX依赖线性混合模型进行参数估计(线性法)。每个方法都有其优缺点。NLMIXED的优点是它更加准确，产生真实的对数似然拟合模型。用户可以有相当大的弹性去定义似然函数。与之相反的是，GLIMMIX对固定效应和协方差参数的估计可能不是无偏估计，尤其是当所分析的数据是二项分布时。

GLIMMIX进行Wald-type检验和生成相应可信区间，嵌套的模型不及真实似然比检验精确。估计不精确换来的是GLIMMIX可以拟合不同类型的模型，随机效应的数量可以有多个，也可以设置拟合的选项。例如，GLIMMIX允许多个嵌套的，交叉的随机效应，但是NLMIXED所能处理的随机效应少于5个。

此外，GLIMMIX允许用户使用REML(restricted maximum likelihood)的方法，NLMIXED过程则不能用REML，只能用 ML(maximum likelihood)。GLIMMIX也支持以模型为基础的对标准误的Sandwich estimation，而NLMIXED只支持基于模型的标准误。即使方差函数错误，Sandwich estimation也能提供一致的结果。但是，正如前面所提及的，GLIMMIX要求反应变量服从指数族分布，而NLMIXED允许用户写出自己的函数。

这两个过程步另外一个不同是初值的设定和应用。NLMIXED，用户必须先产生参数的初值然后把初值代入SAS程序中。一般地，可以使用PROC MIXED或PROC GENMOD来产生NLMIXED的初值。与之对照的是，GLIMMIX使用的是一个双迭代方案。参数的初值来自于线性混合模型，而此初值又用来拟合线性模型。对于用户而言，GLIMMIX不需要费力去设定初值。因此在某些情况下，对模型的控制缺乏也带来一些不足。最后的参数估计对初值非常敏感，如果设定不好，很可能会导致模型不收敛。NLMIXED过程可以允许用户去定义初值，因而也给模型的收敛提供了更多的机会。积累初始值的选择经验、判断是否满足收敛条件及模型评价的标准是非线性分析的关键〔5，6〕。

总之，NLMIXED更适合相对简单，反应变量只有两个水平，随机效应的数量少的情况。当二分类数据需要精确的协方差参数估计，要求用户自定义响应分布，或需要使用似然比检验比较嵌套模型时，可以考虑使用NLMIXED。NLMIXED更适合二项分布数据分析。GLIMMIX则更适合随机效应数量多于两个以上的复杂模型。本例中用NLMIXED分析数据显然更加适合。

1．王全众．两类分析相关数据的 logistic回归模型．统计研究，2007，24(2):81-83．

2．陈卫中，杨晓虹，陈朝琼，等．非线性混合效应模型在交叉设计等级资料分析中的应用．成都医学院学报，2007，2(3-4):181-183．

3．李丽霞，郜艳晖，张丕德，等．广义线性混合效应模型及其应用．现代预防医学，2007，34(11):2103-2104．

4．罗天娥，刘桂芬．重复测量资料非线性混合效应模型应用与实现．中国卫生统计，2006，23(2):104-107．

5．Flom PL，McMahon JM，Pouget ER．Using PROC NLMIXED and PROC GLMMIX to analyze dyadic data with a dichotomous dependent variable．SASGlobal Forum 2007 Proceedings:Paper 179．

6．SAS Institute Inc．SAS/STAT Ⓡ 9.2 User’s Guide．Cary，NC，USA:SAS Institute Inc．，2008，4337-4340．

附录

用非线性混合效应模型PROC NLMIXED分析数据，相应的SAS程序为:

proc nlmixed data=mpr3 alpha=0.05 corr gconv=1e-10;

parms beta0=0.3855 beta1=－0.1599 beta2=0.07278 s2u=0.1709;/*设定参数初值*/

eta=beta0+beta1*treat+beta2*period+u;

expeta=exp(eta);

p=expeta/(1+expeta);

model question1～binary(p);

random u～normal(0，s2u)subject=patient;

ods output parameterestimates=para;

run;

用广义线性混合效应模型PROC GLMMIX分析数据，相应的SAS程序为:

proc glimmix data=mpr3 order=internal;

class patient treat period;

model question1(ref=first)=treat period/solution link=logit dist=binary;

random intercept/subject=patient gcorr;

lsmeans treat/diff=control(“－0.5”)oddsratio cl alpha=0.05;

lsmeans period/diff=control(“－0.5”)oddsratio cl alpha=0.05;

ods output parameterestimates=solf1;

run;