稳健主成分回归及其医学应用*
2011-03-11刘伟新郭东星
刘伟新 郭东星
主成分回归(principal component regression PCR)可用于处理数据中的自变量多重共线性问题,而这个问题在医学资料的数据分析中经常会出现。但是,当数据中存在异常点时会影响主成分回归模型的建立,在进行主成分回归分析时除了可以进行异常点的诊断〔1-2〕外,本文将再介绍一种稳健主成分回归方法来解决这个问题。
原理和方法
1.稳健主成分分析(ROBPCA)〔3〕
ROBPCA(robust principal component analysis)是一种稳健主成分分析的新方法。其结合了投影寻踪(projection pursuit)的思想〔4,5〕和稳健的协方差矩阵〔6,7〕估计的思想。
步骤一:降低数据空间维数
设原始数据为Xn,p。n表示观测样本数,p表示自变量的原始数目。通过中心化数据矩阵的奇异值分解,产生
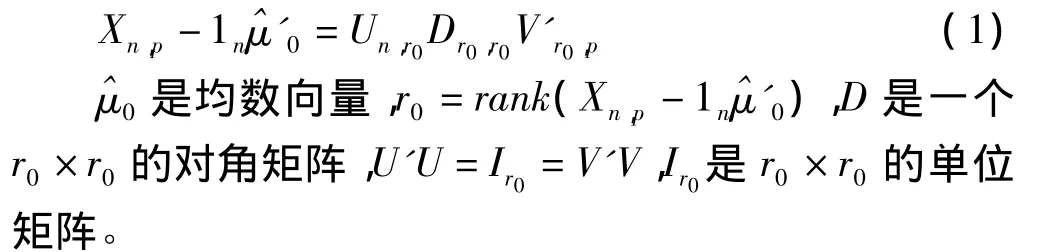
令Zn,r0=UD,变成新的数据矩阵,这个奇异值分解就是数据在V中的r0列所占据的子空间中的仿射转置,并且不会失去任何信息。为了方便起见,新的数据仍然用xi来表示。
步骤二:找到h(h<n)个‘最小异常值’的数据点
事先不知道异常点的数目,就让h=max{[αn],[(n+kmax+1)/2]},kmax代表将要被计算的主成分的最大数目,默认为10。参数α在0.5和1之间选择。默认时α=0.75。
(1)对每一个数据点xi,计算它的异常值(outlyingness),从中找到h个具有最小异常值的数据点,

(2)用^μ1和S0来代表H0中的h个观测点的均数和协方差矩阵。协方差矩阵的特征值按降序排列,而且特征向量被相应地标记。则

L=diag(~l1,…,~lr),是特征值的对角矩阵,r≤ri
协方差矩阵S0决定在未来的分析中,将要保留的主成分的个数k0(k0≤r)。在这过程可以用多种方法达到这个目的,例如,可以观察特征值的单调递减的一个斜线图,或者能利用累积贡献率的选择标准。
(3)将数据点投影到S0的前k0个特征向量所在的子空间上。即令:
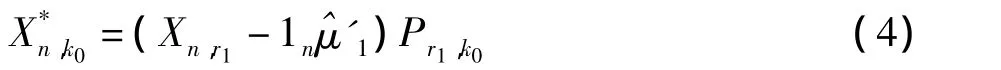
这里Pr1,k0包括了(3)中的P0的前k0列。步骤三:利用MCD估计值〔7〕,稳健地估计X*
n,k0中的数据点的方差-协方差矩阵。
需要找到h个数据点,使它们的协方差矩阵有着最小的行列式。利用由步骤二得到的异常值测量(2)

(4)将P2的列转换回原始空间,产生最后的稳健特征向量矩阵Pp,k。最后稳健中心^μ通过将^μ5转换回原始空间来获得,而最后的p维秩为k的稳健分散矩阵 S 由 S=Pp×kLk×kP'p×k给出。公式(8)中的得分在Rp中可以写为Tn×k=(Xn×p-1n^μ')Pp×k。
稳健主成分分析的部分至此完成。
2.稳健回归法则-LTS(least trimmed squares〔8-10〕)
在稳健主成分回归中,用重新加权的LTS法,众所周知,最小二乘法回归是将残差平方和最小化。对于LTS方法,残差平方和被残差平方的修剪的和所代替。残差平方由低到高排列,然后从最低的残差到排

^y-i,k是主成分数目为k时,观测点i暂时作为验证样本时从已建模型中获得的预测值。这时具有最小的RMSECV值所对应的k被认为是最优的数目。
在稳健主成分回归中,因为不想在RMSECV值中包括异常点的预测误差,所以我们用稳健的RMSECV值
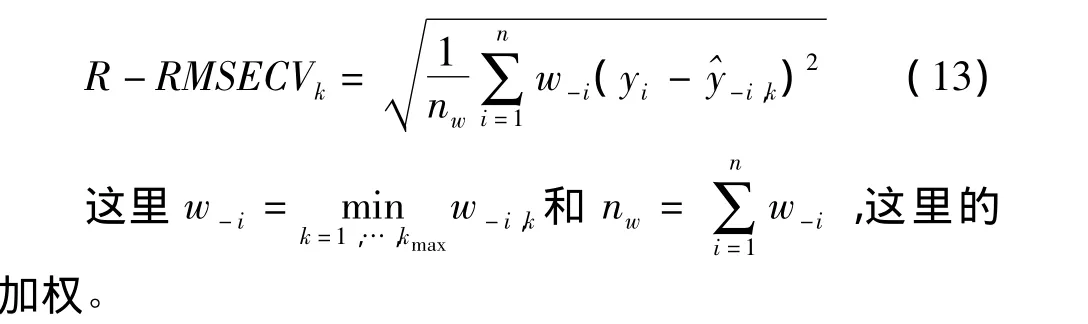
w-i由上面稳健回归时的公式所得到。
由此,具有最小的R-RMSECV值所对应的k被认为是最优的数目。
(2)稳健的R2值
n
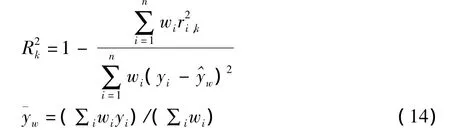
实例与分析
采用17所医院的人力利用情况及有关医院任务的资料〔1〕,其中,X1为平均每天住院人数;X2为每月X线照光人数;X3为每月占病床天数;X4为服务范围内人口数(千人);X5为每名病人平均住院天数;Y为每月使用人力(小时)。以下结果采用SAS 8.0和MATLAB 7.1软件编程实现。
1.常规描述分析和共线性诊断见表1,表2。

表1 17所医院的人力利用及医院任务情况的简相关矩阵
表1中可见,X1与 X2,X3,X4的相关系数、X2与X3,X4、X3与X4的相关系数均大于90%,提示自变量间可能有多重共线性存在。

表2 17所医院的人力利用及医院任务情况的共线性诊断
在表2中可以看出,条件指数11.416,33.881,390.423均大于 10,对应的方差比 0.728,0.944,0.999,0.998大于0.50,因此确定自变量之间存在多重共线性。进行稳健主成分回归分析。
2.进行主成分个数选择
图1,2中表示,选择第一,第二主成分后稳健的R-RMSECV值最小,且稳健的R2值最高,所以选择第一和第二两个主成分。
3.稳健主成分分析ROBPCA结果:稳健均数估计值^μ=
[81.2328 10595.3629 2435.8449 65.4358 5.4438],稳健特征值为[84131696.2849 517807.0308],稳健

数据中心化,可以计算得到稳健的主成分。

图 1 稳健的 RMSECV 值(1912,757.4,851,1023,639.2)

图 2 稳健的值(0.9871,0.9960,0.9951,0.9963,0.9964)
4.两个主成分与因变量的稳健回归结果
参数估计值^φ1=0.2256,^φ2=0.6436,截距=2683.029,R2=0.99435,所以方程为 ^Y=2683.029+0.2256T1+0.6436T2
反代回原始自变量得:
^Y=34.9719+0.0219X1+0.0946X2+0.6751X3+0.0018X4+0.0005X5。
5.稳健主成分回归还将产生可以诊断异常点的诊断图:

图3 稳健主成分分析的主成分诊断图
由图3 可见,点10,14,15,16,17 为异常点。其中点14,15,17为无影响PCA杠杆点,点10为正交异常点,点16为有影响PCA杠杆点。
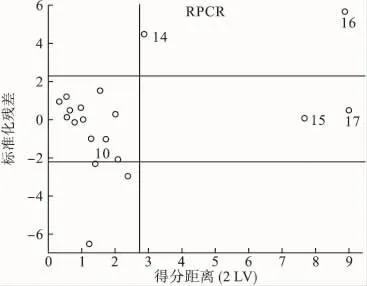
图4 稳健主成分回归的回归方面的异常点诊断图
由图4可见,点15,17为无影响异常点,点9,10为垂直异常点,点14,16为有影响异常点。
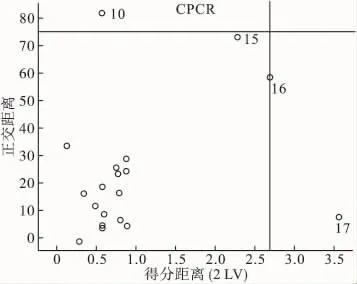
图5 经典的主成分分析的主成分诊断图
由图5可见,只有点10,17被诊断为异常点。

图6 经典主成分回归的回归方面的异常点诊断图
由图6可见,只有点9和点16,17被诊断为异常点,其他三个异常点并没有被诊断出来。
讨 论
本文所介绍的稳健主成分回归方法是由两部分稳健方法组成:稳健主成分分析方法ROBPCA和稳健回归方法即重新加权的LTS法。这两种方法均为目前最新的非常稳健的方法。这两部分方法的失效点均达到50%。这种稳健主成分回归方法计算速度快,并且对于低维和高维的数据都能够处理。而且既可以用在有异常点的数据,也可以用于没有异常点的数据。在实例分析中表明,当数据中包含异常点时,与经典的主成分回归相比较,此方法得到了稳健的估计值,并且诊断图对于确定异常点也非常有用。
通常在诊断出异常点以后,不能简单地将异常点删除,因为这样做可能将异常点携带的一些有用的信息丢失,所以应该对不同情况的异常点给予不同处理。如果证实是数据录入错误,可以删除。而多数情况下,剔除只是一种识别数据是否异常的方法,不是诊断分析的最终目的。对于处理的方法,除了有本文提到的稳健估计方法外,还需要以后进一步的研究和探讨。
1.郭东星,刘伟新.主成分回归中异常点的稳健诊断.中国卫生统计,2008,25(1):31-34.
2.刘伟新,郭东星.主成分回归中异常点的二步诊断法及其医学应用.现代预防医学,2007,34(13):2423-2425.
3.Mia H,Peter JR.ROBPCA:a new approach to robust principal component analysis.Technometrics,2005,47:64-79.
4.Jolliffe IT.Principal component analysis.New York:Springer,1986.
5.Li G,Chen Z.Projection-Pursuit approach to robust dispersion matrices and principal components:primary theory and Monte Carlo.Journal of A-merican statistical association,1982,80:759-766.
6.Rousseeuw PJ,Van DK.A fast algorithm for the minimum covariance determinant estimator.Technometrics,1999,41:212-223.
7.Croux C,Haesbroeck G.Influence function and efficiency of the minimum covariance determinant scatter matrix estimator.Journal of Multivariate A-nalysis,1999,71:161-190.
8.Pell RJ.Multiple outlier detection for multivariate calibration using robust statistical techniques.Chemometrics and Intelligent Laboratory Systems,2000,52:87-104.
9.Rousseeuw PJ,Leroy A.Robust regression and outlier detection.New York:John wiley,1987.
10.Walczak B.Outlier detection in multivariate calibration.Chemometrics and Intelligent Laboratory Systems,1998,28:259-272.
