复杂抽样下截取因变量回归系数方差估计的模拟研究*

山西医科大学公共卫生学院(030001) 王晓荣 王 彤

在一些临床观察中，研究者常将能够代表人群健康状况的某个指标作为因变量来分析其影响因素，然而在测量该指标水平时由于仪器的检测极限问题，在某个水平之上或之下的值我们观测不到，在数据收集时通常会用这个极限水平的值来代替那些我们观测不到的数值。这里的因变量在理论上是连续的，但由于测量时受到某种限制，在某一点上被删失或称截取(censoring)而用界值代替，因变量成为连续分布和离散分布的混合分布〔1〕。对此类数据可以采用tobit回归，或更普通的截取回归模型进行分析。实际工作中对于所涉及的研究总体较大的调查，在研究设计时往往会整合简单随机抽样、分层抽样、整群抽样等多种基本的抽样技术形成多阶段复杂抽样，涉及截取因变量数据的调查也不例外。如果此时仍采用常规数据分析方法来分析复杂的截取数据，忽略分层、整群及不等概率抽样等因素所带来的设计效应，即使样本量足够大，也可能得出错误的推断结论〔2，3〕。故本次研究将模拟复杂抽样设计下的截取数据，并用泰勒级数法估计待估参数及其标准误，将其与不考虑复杂抽样设计之结果进行比较。

基本原理与方法

1.tobit模型的基本形式:

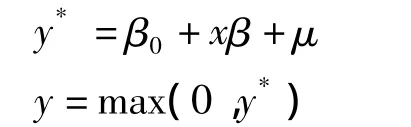
该方程意味着当y*＞0时，所观测到的变量y=y*，当y*≤0时，则y=0。以上是将截取点设为零，事实上截取临界点可以为ci，ci可以对所有的i都是一样的，但在多数情况下将随着i的不同而变化，并且ci既可以从左截取，也可以从右截取，还可以两边同时截取。在这些更广泛的情况下我们称模型为截取回归模型。例如医学随访研究中常遇到的生存分析数据大多数属于右截取情况，而tobit模型事实上是截取回归模型在左端截取点为0时的特殊情况〔1〕。

2.参数估计

在tobit回归模型中，当误差满足正态同分布时，即u|x～N(0，σ2)，估计回归系数常用的是最大似然法，似然函数的表达式如下:

上述方法是针对于简单随机样本而言的，对于复杂抽样数据应考虑更恰当的处理方法，如本次研究采用的参数及其方差估计方法是泰勒级数法。泰勒级数法的基本思想就是通过泰勒级数展开式用线性估计去逼近非线性估计，给出方差这个非线性估计量的一个近似估计。然而泰勒级数法本身不能独自地用于方差估计的构造，它只是提供了非线性估计量的一种线性逼近算法，有时需要结合其他的复杂抽样(刀切法、平衡半样本法等)技术进行分析〔4，5〕。

(1)泰勒级数展开式如下:

对于非线性函数Y=f(x)，x0为一个给定点，则f(x)在x0的泰勒级数展开为:

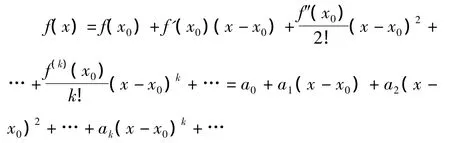
其中，a0，a1，a2，…，ak，…为常数，如果仅保留常数项和一阶导数项，就可以得到非线性函数f(x)在定点 x0处的线性化估计〔4〕。

(2)泰勒级数近似法估计方差〔6〕

现以分层整群抽样为例探讨复杂抽样条件下tobit回归系数的方差估计。假设现在有一组分层整群数据，共有H个层，每个层中有M个群，每个群内有B个观察单位。从每个层内抽取m个群进行观察。

在tobit回归模型中，假定回归系数B与变量y和x的关系用下面的函数表示:

2.2.2 概率敏感性分析结果 由成本效果可接受曲线（图3）可以看出，当WTP小于60 000元时，仙灵骨葆胶囊具有成本效果优势的概率更高；当WTP达到60 000元时，芪骨胶囊成为优选方案的概率为52.5%；当WTP超过60 000元时，芪骨胶囊具有成本效果优势的概率更高。

B=f(y，x)

如果函数f(y，x)的二阶偏导数存在，运用泰勒级数展开式中的线性项就可以得到一个近似的线性表达式。

这样就将一个非线性函数比值的方差估计转变成为由y和x的方差和协方差所组成的线性函数。

设计效应值越大，表明它的效率越低，若deff＞1，表明所考虑的抽样设计的效率比简单随机抽样低，若deff＜1，表明该抽样设计的效率比简单随机抽样高〔4〕．

模拟分析

1.模拟条件

预模拟一个10 000例的总体，总体中有两个层，第一层中有6 000例观察对象，将这6 000例观察对象完全随机地分配到100个群中，每群60例。第二层中有4 000例观察对象，将这4 000例观察对象完全随机地分配到80个群中，每群50例。这样分群可以使群内方差与总体方差近似相等，使得群内相关系数近似为0，保证群内数据的异质性〔4〕。

2.左截取数据的模拟及其参数模型分析结果

我们需要模拟三个变量:分别为x、y、u，其中x为自变量，y是应变量，u是误差项，y=1+x+u，u取自均值为0标准差为1的正态分布。自变量x的产生如下:第一层的数据是来自(0，1)的均匀分布，例数为6 000。第二层的数据是来自均数为0.5，标准差为1的正态分布中随机产生，例数为4 000。然后我们按照等比例抽取的方式，每层均随机抽取1/10的群作为样本(即第一层中抽取10个群，第2层中抽取8个群)，重复上述过程，模拟1 000次，得到1 000个样本，用这1 000个样本的数据拟合左截取tobit回归模型，每个样本均可计算出一个回归系数以及其标准误，最后计算出这1 000个样本的回归系数的均数和标准差。在

(3)设计效应

为比较不同抽样设计的效率，基什(L．Kish)提出了设计效应的概念，设计效应(design effect，简记为deff)指的是一个特定的抽样设计估计量的方差对相同样本量下简单随机抽样的估计量的方差之比，计算公式如下:模型拟合过程中，我们不断变换截取数据的比例，回归系数的均数及其标准误会随着截取数据比例的改变而改变。

我们采用按比例截取方式来截取数据，截取比例分别为5%、10%、15%，其结果见表1。

表1 不同截取比例下左截取tobit模型回归系数的模拟分析

从表1中可以看出，回归系数的均数和标准误随着截取比例的变化而变化，随着截取比例的增大，从5%逐渐增大至15%，考虑抽样特征和不考虑抽样特征这两种情况下，左截取tobit回归模型的回归系数的均数越来越偏离真值1，且标准误逐渐增大。当截取比例固定不变时，考虑抽样特征的情况下回归系数的标准误要明显低于不考虑抽样特征，将数据作为完全随机处理的情形。

左截尾数据比例为5%、10%、15%时，tobit模型的设计效应deff分别为0.8539、0.8937和0.9089，我们可以看出截取数据比例越小，模型的估计效率越高，估计结果真实性和准确性也越高。

3.右截取数据的模拟及其半参数模型分析结果

首先生成服从(0，1)均匀分布的随机数S，令生存函数S(t)=S，第一层数据采用服从均数为0.5，标准差为1的正态分布数据作为自变量x，例数为6 000，第二层的数据采用服从均数为0.1，标准差为0.5的正态分布数据作为自变量x，例数为4 000．令总体回归系数b=1，λ=1，利用来计算服从参数为λ的指数分布的生存时间t。然后我们按照等比例抽取的方式，每层均随机抽取1/10的群作为样本(即第一层中抽取10个群，第2层中抽取8个群)，重复上述过程，模拟1 000次，得到1 000个样本，用这1 000个样本的数据拟合COX比例风险模型，每个样本均可计算出一个回归系数以及其标准误，最后计算出这1 000个样本的回归系数的均数和标准差。在模型拟合过程中，我们不断变换截取数据的比例，回归系数的均数及其标准误会随着截取数据比例的改变而改变。

我们采用按比例截取方式来截取数据，截取比例分别为5%、10%、15%，其结果见表2。

从表2中可以看出，回归系数的均数和标准误随着截取比例的变化而变化，随着截取比例的增大，从5%逐渐增大至15%，考虑抽样特征和不考虑抽样特征这两种情况下，COX比例风险回归模型的回归系数的均数越来越偏离真值1，且标准误逐渐增大。当截取比例固定不变时，考虑抽样特征的情况下回归系数的标准误要明显低于不考虑抽样特征，将数据作为完全随机处理的情形。

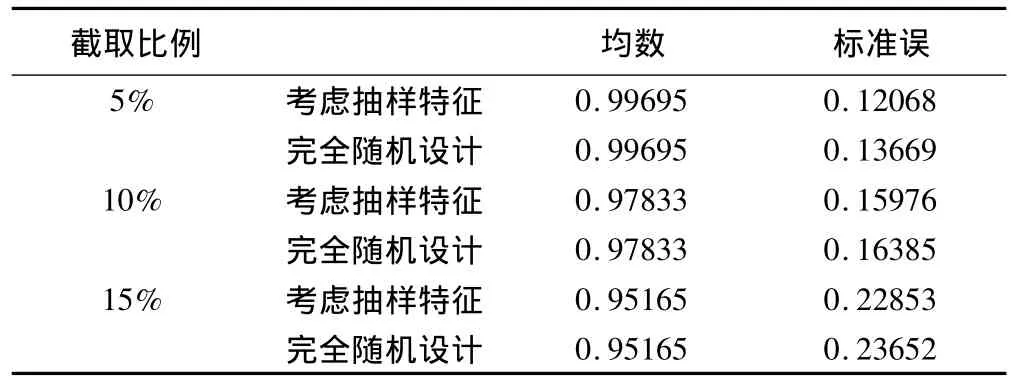
表2 不同截取比例下COX比例风险模型回归系数的模拟分析

右截尾数据比例为5%、10%、15%时，tobit模型的设计效应 deff分别为 0．8827、0．9489 和 0．9662，我们可以看出截取数据比例越小，模型的估计效率越高，估计结果真实性和准确性也越高。

从上述模拟结果可以看出，不管是左截尾还是右截尾数据，考虑抽样特征后模型回归系数的标准误明显低于不考虑抽样特征的情形。因此，对于大规模的抽样调查，如果抽样框清楚明确，在进行数据分析和处理时应尽可能的将抽样特征考虑在内，如忽略分层整群等抽样特征而一味地用简单随机假设条件下的方法来计算其回归系数的标准误，可能在一定程度上损失设计原有的估计效率〔4，5〕，这样有时就会使得有统计学意义的因素变得无统计学意义。

讨 论

1.截取数据的tobit回归模型在医学研究中的应用日渐广泛，本次模拟研究中模型误差项满足正态分布，且方差齐，因此在不考虑抽样特征的情况下采用最大似然估计来估计模型中的参数，但是最大似然估计的使用是有严格条件限制的，需要已知模型中数据误差项的分布形式。如果我们调查所得的数据误差项的分布未知，使用最大似然估计很可能得出错误的结论，这种情况下应考虑限制条件相对较松的半参数和非参数估计方法〔1〕。

2.从模拟试验中可以看出，随着截取数据比例的增大，模型回归系数的均数越来越偏离真值，且标准误逐渐增大，当截取数据的比例固定时，考虑抽样特征情况下模型回归系数的标准误要低于不考虑抽样特征的情形。因此在应用截取回归模型处理问题时，首先需注意截取数据在整体数据中所占的的比例，如果截取数据的比例太大，直接使用该模型可能会得出有偏差的结论。其次，如果数据的抽样框清楚明确，在数据分析和处理时应充分利用数据的抽样特征，这样得出的结果更加真实可靠。

3.本次数据模拟时是将两层的数据完全随机地分到各个群中，群内相关系数(intra-class correlation coefficient)接近于0，此时可以将群效应忽略，仅考虑分层的影响，因此考虑抽样特征后，其回归系数的标准误要低于完全随机的情形，但是在实际应用过程中，我们遇到的数据中群内相关系数往往是不可能忽略的，有时甚至很大，这样会明显降低估计效率，很多情况下会使设计效应远远大于1。这种情况下，笔者认为可结合非独立数据的建模方法来解决，如GEE等混合效应模型。

4.tobit模型可以用于各种截取数据的处理和分析。通常使用的tobit模型中假定误差项是服从正态分布的，但它还可以是指数分布、威布尔分布、对数正态分布等〔7〕。事实上，在医学领域中，对于常见的右截取生存分析数据，我们只要指定tobit模型中的误差项满足指数分布或威布尔分布，就可以用来处理右截取生存分析资料，这样也使tobit回归模型在医学中的应用得到了延伸。

5.本次研究复杂截取数据相关参数的方差估计采用的是泰勒级数近似法，对于大规模复杂抽样调查来说，泰勒级数线性法一般能给出真实有效的近似方差估计。且只要偏导数存在，线性法总能给出统计量的方差估计量，但并非所有的统计量均能表示为平滑的线性函数。如果出现这种情况，可以考虑使用其他的数据处理技术如:平衡半样本法，刀切法等技术来处理〔4，6〕。刀切法和平衡半样本法都属于样本再利用法，可以重复利用一个样本的信息，由于这些方法不依赖于估计量的形式，可以用于估计任何非线性估计量的方差，主要适用于总体中有多个层，每个层中抽取两个群的情况，也可以用于更复杂的抽样设计的估计量的方差估计〔8，9〕。

1．薛小平，史东平，王彤．受限因变量模型及其半参数估计．中国卫生统计，2007，24(2):211-213．

2．Rao JNK，Wu CFJ．Resampling inference with complex survey data．Journal of the American Statistical Association，1988，83，401，231-241．

3．Lee ES，Forthofer RN．Analyzing Complex Survey Dat，Sage Publications Inc，2005．

4．冯士雍，倪加勋，邹国华．抽样调查理论与方法．北京:中国统计出版社，1998．

5．Wolter KM著，王吉利，李毅主译．方差估计引论．北京:中国统计出版社，1998．

6．Risto Lehtonen，Erkki Pahkinen．Practical methods for design and analysis of complex surveys．John Wiley$Sons Ltd，The Atrium，Southern Gate，Chichester，West Sussex PO198SQ，England，2004．

7．SASInstitute Inc．SAS/STAT0 9．1 User’s Guide．Cary，NC:SASInstltute Inc，2004．

8．Thomas Lumley．Analysis of complex survey samples．Department of Biostatistics in Univers-ity of Washington，2004．

9．KF Rust，Jnk Rao．Variance estimation for complex surveys using replication techniques，Statistical Methods in Medical Research，1996，5(3):283-310．