非饱和土渗流-变形耦合的数值分析

吴礼舟,黄润秋

(成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)

非饱和土渗流-变形耦合的数值分析

吴礼舟,黄润秋

(成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)

基于一维非饱和土的渗流-变形控制方程,采用Flex PDE(Partial differential equation)软件对该耦合方程组进行求解分析。该方法突破了解析法对非饱和土导水系数函数的特殊限定,适用于任意的土-水特征曲线表达式;还可考虑到饱和时的渗透系数以及孔隙率是变量。与解析解相比,该数值解表现较高的精度,具有解决非饱和土耦合问题的可行性。计算分析表明,非饱和土渗流-变形耦合作用对暂态孔隙水压力分布产生重要的影响,在降雨入渗过程中需考虑土体渗流-变形耦合的影响。降雨初期,位移随着时间明显增大,地表出现下沉,考虑耦合效应的孔隙水压力慢于非耦合情况,原因是H值为正的。随着降雨持续时间的增大,地表下沉的速度减缓,到最后变形开始稳定。位移的变化快慢与孔隙水压力变化规律相同。地表沉降量还与初始孔隙水压力分布以及H值密切相关。饱和时的渗透系数以及孔隙率对非饱和土降雨入渗以及稳态流的分布产生影响,但对其地表变形产生的影响微弱。

非饱和土;渗流-变形耦合;降雨入渗;数值分析

非饱和土的渗流-变形耦合一直岩土工程界的一个研究热点。土坡、路基填土以及垃圾与核废料填埋场大都处于非饱和状态。伴随着人类活动的深入,越来越多的非饱和土工程问题亟待解决。例如降雨等诱发的边坡失稳、坝基坍塌等地质灾害现象等。非饱和土是固-液-气三相复合介质,物理性质复杂。降雨入渗或水位涨落过程中,非饱和土中渗流与变形一直是相互作用、相互影响的[1-2]。需要研究入渗的瞬态渗流场、变形以及各种边界条件的影响。如何定量描述非饱和渗流过程中流动与骨架变形的相互作用,也是当今科研的难点[2]。因此,从渗流-变形耦合分析的角度上探讨非饱和土渗流以及变形问题具有较高的科研以及生产实践价值[2]。

项目化教学设计理念已经广泛用于其他课程的教学中，并取得了较好教学效果，为此必须探索如何将它应用于《建筑施工技术》中高职衔接课程的教学设计，围绕真实的工程项目的施工全过程，进行该课程的整体教学设计，分段组织教学和实现课程的培养目标。作为任课老师应经常深入施工现场，积累现场施工各个阶段的图片、资料，并积极创造条件参与施工组织和验收等环节，增强对施工现场的直观认识与理解。

护理后，中医护理管理组的51例患者中有48例患者能够合理用药，占总人数的94.1%；有46例患者能够对饮食进行控制，占总人数的90.1%，有40例患者能够科学运动，占总人数的78.4%，而传统护理组中有35例患者能够合理用药，占总人数的68.6%，有40例患者能够对饮食进行控制，占总人数的78.4%，有32例患者能够科学运动，占总人数的62.7%。两组患者自我管理行为比较，P＜0.05。

饱和-非饱和土的多场耦合研究引起众多学者的兴趣[2-9]。白冰对饱和多孔介质热-水-力耦合响应的一维情形进行研究,给出温度、孔压和位移等的解析表达式[3]。吴礼舟等也给出非饱和土渗流-变形耦合的解析解[4]。张玉军从水-气-热三场耦合的角度上分析了孔隙介质中各组分的渗流与变形问题[5]。Thom as提出了可变形的非饱和土热,水和气转化的理论表达式[7]。廖红建等对水库堤坝进行了非稳定渗流场的数值模拟,并对土体固-液耦合研究进行了探讨[8]。卢再华、陈正汉等建立了一个非饱和膨胀土的弹塑性损伤本构模型及相应的固结模型,对该边坡进行了三相多场耦合问题的数值分析,较好地揭示了膨胀土边坡在气候变化条件下逐渐发生失稳滑动的机理[9]。

非饱和土渗流-变形的耦合的解析解多要求形式简单的土-水特征曲线表达式,局限于饱和土渗透系数为常数的条件。而实际上,饱和时渗透系数与应变有关,是变量。基于非饱和土渗流-变形的耦合模型,采用应用广泛的V-G模型,利用美国的商业软件Flex PDE软件研究一维非饱和土渗流-变形的数值解,试图分析耦合作用对非饱和土渗流与变形的影响。

1 变形渗流耦合模型

为了分析渗流和变形耦合问题,作出如下假设：1)土是均一的,各向同性的弹性材料;2)土结构是可变形的,水是不可压缩的;3)不考虑土-水特征曲线的滞后性;4)在土中孔隙气压力为一常值。

对非饱和土渗流-变形耦合控制方程进行修正,为[4]：

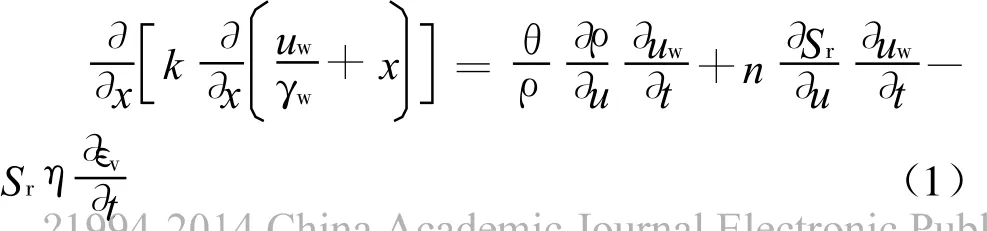
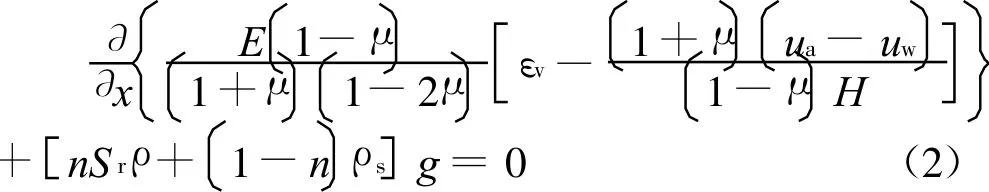
式中：是孔隙水压力;εv为体积应变,对于一维问题,εv=εx;x为高程;k为非饱和土的渗透系数;ρ为水密度;g为重力加速度;γw=ρg为水的自重,εs为固体密度;Sr为饱和度;n为孔隙率;为初始的孔隙率。η=(1-n)2/(1-)。E为杨氏模量;t为时间;(ua-uw)为土吸力;ua为孔隙气压力;μ为泊松比;E为净正应力变化相关的土的弹性模量;H为吸力变化相关的土的弹性模量。

假设不考虑水的压缩性和重力项,式(1)、(2)则写成

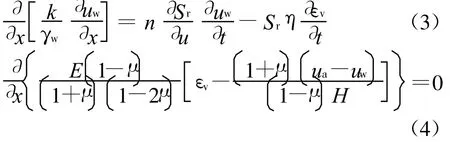
式(4)中,应变是uw的函数,而uw是随时间而变,因而应变也是时间的函数。

土-水特征曲线对于研究非饱和土水力学性质是非常重要的。Van Genuchten模型是一种常见的模型。该模型不仅拟合效果较好,并能和土的性质联系起来,从土本身特性上找到其含义,而得到广泛应用。Van Genuchten模型的表达式为[10]：

式中ks为饱和土的渗透系数(为了解析需要,假定为常数);α为去饱和系数。

饱和度的函数为：

相对应的非饱和土导水率为

底部边界通常位于固定的地下水位,即u0=0; ε0=0。上边界通常分为流量和压力边界。地表边界的应变为自由边界。这里仅考虑了流量边界,其表达式为

在进行地表施工作业时，地表浅层土通常是施工的重要目标。但是地表浅层土会受温度、土体、气候等多方面因素的干扰，因此其水分场与温度场都会不断改变，而且相互影响。土壤的温度在发生改变时，土体内部的水分也会相应变化，这一变化进而会导致其自身导热系数与比热的改变，最终引起土壤温度场与传热能力的变化。在温度降低的时候，土壤会迅速凝固并释放热能，此时水分也会相应发生移动，那么土体的温度场就会产生变化。［2］

孔隙率也是应变的函数

其中,ks0是个恒定的值。

假定土层均一,对于一维问题,沿着x轴,长度为l。非饱和土渗流-变形耦合问题通常涉及初始条件和边界条件。初始的孔隙水压力和应变表达为

图3为非饱和土渗流-变形耦合作用下位移分布图。图3显示了,降雨初期阶段,位移随着时间明显增大,地表出现下沉。这是由于H大于0[4]。随着降雨持续时间的增大,地表下沉的速度减缓,到一定值后,变形开始稳定。位移的变化快慢与孔隙水压力变化情况相同。从图2可看出,降雨诱发的地表下沉最终估算量约为0.004 3m。地表沉降量还与初始孔隙水压力分布有关,还与非饱和土的H值密切相关。

边界条件由底部和地表边界条件组成,底部边界的表达式为

可见“醉鬼”不醉，只是以醉态示人。至于为何如此，有人说是他藏形隐色，掩饰真功以防暗算的一种做法；有人说是他为了免除权贵骚扰，故意所作的玩物丧志饮酒误事的假象。

江苏省明确规定“结合我省新一轮药品集中采购工作进展，第二批竞价采购、议价采购、限价挂网采购药品，自采购结果执行之日起同步执行‘两票制’”，照此实施，留给药品批发企业的时间十分有限，其现有库存中不符合“两票制”的药品，在“两票制”全面执行后应如何处理？如这类库存药品不能销往公立医疗机构，企业将面临巨大的经济损失。

将式(15)、(16)代入式(1)、(2),采用Fourier积分变换,可获得耦合控制方程的解析解。

2 验 算

为了验证PDE软件计算非饱和土渗流-渗流耦合模型的精度,采用了解析解与数值解进行比较。Van Genuchten模型虽然应用广泛,而对于获取耦合控制方程的解析解却有局限,将其代入耦合方程难于获取解析解。这里利用指数函数以及Kirchhoff变换,假定进气值ψae=0 kPa,Gardner的非饱和土渗透系数可表示为[12]

根据Boltzman模型[13],体积含水率与土吸力之间的关系,基于体积含水率与饱和度的关系Sr= θ(uw)/θs,则得到

对比激光刻蚀区域与未刻蚀区域的力学性能可以发现，3种铝合金的力学性能也基本相同，最大差异出现在LD10的抗拉强度，刻蚀后不过降低了3.7%。这进一步说明了刻型时激光不会对基体产生影响。

其中：q可为常量,也可为变量,须满足q＜ks。当q＞ks时,式(14)变成孔隙水压力边界。

表1 非饱和入渗分析的参数值

长度l为10 m,初始孔隙水压力分布用式(10)定义,可为任意分布,这里为线性分布。底部边界为稳定的地下水位,即u0=0。地面边界的降雨强度为q。相应参数见表1。图1是解析解与数值解的比较。数值解是采用PDE软件分析的,将式(15)、(16)代入耦合控制方程(1)、(2)而得到的数值解。在4、12 h时的数值解与解析解的差值均小于1%。图1表明Flex PDE软件计算非饱和土渗流-变形问题有较好的准确性。用PDE软件分析非饱和土渗流-变形耦合控制方程,具有较强的适宜性。不仅适用于Gardner模型,还适用于其他模型。且能考虑到饱和时渗透系数是变量。

图1 数值解与解析解的孔隙水压力比较

3 算例分析

解析方法适用范围有限,对于Van Genuchten模型无法获得解析解,因而,这里采用PDE软件分析基于Van Genuchten模型的耦合方程组。表1为计算的参数值。V an Genuchten模型参数分别为：a=0.01 kPa-1,θs=0.4,θr=0.05。初始位移为零,下边界为u0=0。上边界为降雨流量边界。其他参数与验算例子的参数相同。下面分别研究非饱和土的渗流-变形耦合的作用。

图2显示了非饱和土渗流-变形耦合作用下孔隙水压力的分布图。图2中参数分别为：H=2× 104kPa,ks0=3×10-5m/s。在降雨初期,表层的孔隙水压力变化幅度较大,底部的孔隙水压力仍保持不变,因为入渗初期湿润锋从地表慢慢下移,未达到底部。当降雨持续到一定阶段后,孔隙水压力变化速度开始慢下来,t=50 min时的孔隙水压力为-8.87 kPa,而t=100 min时的孔隙水压力为-7.35 kPa。t=50min与t=100 min时地表的孔隙水压力差为0.52 kPa;然而t=10 min与t=50 min地表孔隙水压力相差31.50 kPa。这个表明降雨入渗50min后孔隙水压力分布基本接近了稳定状态。

图2 非饱和土渗流-变形耦合下孔隙水压力分布

式中：ui为初始的孔隙水压力,与x位置有关。εi(x)为初始应变。

图3 非饱和土渗流-变形耦合下位移分布

图4为非耦合与耦合2种情况下孔隙水压力随时间的变化图。参数不变,耦合情况是考虑饱和渗透系数与孔隙均变化的情况,即式(8)、(9)。图4显示耦合效应非常显著,在降雨持续1m in时不考虑渗流-变形耦合的情况下地表孔隙水压力为-78.09 kPa,湿润锋已快速移动到x=10m位置;而此时若考虑耦合作用,则地表的孔隙水压力为-43.08 kPa,湿润锋移动至约x=5m处。在t=1min时非耦合与耦合之间的孔隙水压力差最大达到35.4 kPa。当t=10m in时湿润锋均已到达土层底部,其耦合效应也非常突出,耦合与非耦合2种情况下的孔隙水压力差高达31.1 kPa。在图4中,由于H值为正值,考虑耦合效应的孔隙水压力总是慢于非耦合情况。在降雨入渗过程中应考虑土体渗流-变形耦合的影响。

(3) 除套箍指标较小的试件外，所有试件的滞回曲线比较饱满，变形满足抗震延性需求，表明方钢管再生混凝土柱在高温作用后的抗震滞回性能仍较好，若适当提高套箍指标，性能会更好。

杨鹏说：“我很享受那种万军丛中取上将首级，事了拂衣而去的感觉。”既希望做出丰功伟绩，又不希望被人太多注目，这样的杨鹏，是可爱的。所以，我们很难看到一个张扬的他，只有当你翻开他的履历，试图真正去了解他时，你才会惊奇地发现，这是一个被严重低估的作家——

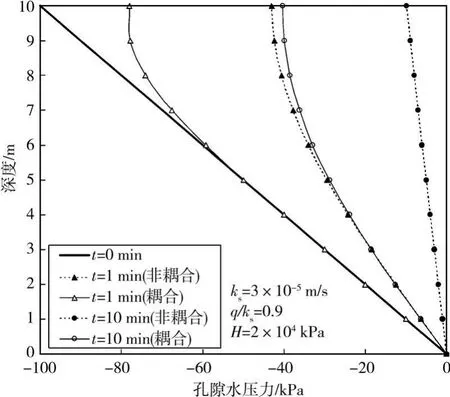
图4 耦合与非耦合的孔隙水压力比较

表2 非耦合与耦合作用下孔隙水压力分布的比较(200 m in)

图5 非饱和土渗流-变形耦合情况下位移变化图

表2显示了t=200min时的孔隙水压力分布。此时不考虑耦合效应地表的孔隙水压力为-9.853 kPa。若考虑耦合效应,当ks、n均不变的情况下,孔隙水压力-5.317 kPa,当ks、n均是变量的情况下,地表的孔隙水压力-7.340 kPa。这些表明耦合效应对孔隙水压力分布产生显著作用,且饱和时的渗透系数以及孔隙率对非饱和土降雨入渗产生影响,其值的变化也影响到稳态流的分布。

技术支持的学习空间是在线教育的基本构成框架，所以教学过程中应用的各类技术和教学理念对于在线教育教师而言，是重要的核心素养。在线教育必须最优化地利用新的泛在技术，提供没有束缚的学习连接。在学习过程中，对于自己的学习管理，在线学习者将承担更大的责任，他们也将要求在线教育技术和在线教育提供者保障他们的学习优先权，并为其学习优先权服务。即在线教育中教师应为熟练的服务提供者，尽可能创造性地利用技术去满足其学习需求和愿望，促进学习者批判性思维和果断利用信息的能力。

图5展示了耦合情况下位移随着时间的变化图。在图5中,虚线表示ks、n不变;而实线表示ks、n为变量。在降雨初始阶段,ks,n是否变化对位移影响不大,尔后时段两种工况下位移的差异微弱增大。总体上ks、n是否变化对非饱和土土体变形产生的影响微弱。

4 结 论

1)研究表明Flex PDE软件计算非饱和土渗流-变形耦合问题的可行性。在降雨入渗过程中非饱和土渗流-变形的耦合效应非常显著,需考虑土体渗流-变形耦合的影响。

2)降雨初期阶段,位移随着时间明显增大,地表出现下沉,这是由于H大于0。随着降雨持续时间的增大,地表下沉的速度减缓,到一定值后,变形开始稳定。地表沉降量还与初始孔隙水压力分布有关,还与非饱和土的H值密切相关。孔隙水压力变化快慢规律与位移的变化情况近似。

3)饱和状态时的渗透系数是变量,其变化对非饱和土降雨入渗产生影响,也影响到稳态流的分布;但对非饱和土土体变形产生的影响微弱。

致谢：本文在完成过程中得到了香港科技大学土木工程系张利民(Limin Zhang)教授的指导,在此向他表示衷心的感谢!

[1]ZHANG L L,ZHANG L M,TANG W H.Rainfallinduced slope failure considering variability of soil p roperties[J].Geotechnique,2005,55(2)：183-188.

[2]徐炎兵,韦昌富,李幻,等.非饱和土渗流与变形耦合问题的有限元分析[J].岩土力学,2009,30(5)：1490-1496.

XU YAN-BING,W EICHANG-FU,LIHUAN,eta l. Finite element analysis of coupling seepage and deformation in unsaturated soils[J].Rock and Soil Mechanics,2009,30(5)：1490-1496.

[3]白冰.循环温度荷载作用下饱和多孔介质热-水-力耦合响应[J].工程力学,2007,24(5)：87-92.

BA I BING.Thermo-hydro-mechanica l responses of saturated porousmediaunder cyclic thermal loading[J]. Engineering Mechanics,2007,24(5)：87-92.

[4]吴礼舟,张利民,黄润秋,等.非饱和土中变形与渗流耦合的一维解析及其参数分析[J].岩土工程学报,2009, 31(9)：1450-1455.

WU LI-ZHOU,ZHANG LI-MIN,HUANG RUNQIU,et al.One-dimensional analytical analysis of coup led deformation and seepage in unsaturated soil and its parameter study[J].Chinese Journal of Geotechnical Engineering,2009,31(9)：1450-1455.

[5]张玉军.核废料处置概念库近场热-水-应力耦合模型及数值分析[J].岩土力学,2007,28(1)：17-22.

ZH ANG YU-JUN.Coupled thermo-hyd ro-mechanical model and relevant numerical analysis for near field of conceptual nuclear waste repository[J].Rock and Soil Mechanics,2007,28(1)：17-22.

[6]K IMJM.A fully coup led finite element analysis of water-table fluctuation and land deformation in partially saturated soils due to surface loading[J].International Journal for Numerical Methods in Engineering,2000, 49：1101-1119.

[7]THOMAS H R,HE Y.Analysis of coupled heat, moisture and air transfer in a deformab le unsaturated soil[J].Geotechnique,1995,45：677-689.

[8]廖红建,姬建,曾 静.考虑饱和-非饱和渗流作用的土质边坡稳定性分析[J].岩土力学,2008,29(12)：3229-3234.

LIAO HONG-JIAN,JI JIAN,ZENG JING.Stability analysis of soil slopes considering saturated and unsaturated seepageeffect[J].Rock and SoilMechanics,2008,29(12)：3229-3234.

[9]卢再华,陈正汉,方祥位,等.非饱和膨胀土的结构损伤模型及其在土坡多场耦合分析中的应用[J].应用数学和力学,2006,27(7)：781-788.

LU ZAI-HUA,CHEN ZHENG-HAN,FANG XIANGWEI,et al.Structural damage model of unsaturated expansive soil and its app licationin multi-field couple analysis on expansive soil slope[J].Applied Mathematics and Mechanics,2006,27(7)：781-788.

[10]VAN GENUCH TEN MT.A closed form equation for p redic ting the hyd rau lic conductivity of unsaturated soils[J].Soil Science Society of America Journal, 1980,44：892-898.

[11]陈成意,宋修海.各向异性弹性孔隙介质中的热-流-变形耦合模型[J].兰州理工大学学报,2009,35(4)：70-73.

CHEN CHENG-YI,SONG XIU-HA I.Coup ledmodels of heat-flow-deformation for porous medium w ith anisotropical e lasticity[J].Journal of Lanzhou University of Technology,2009,35(4)：70-73.

[12]GARDNER W R.Some steady-state solutions of the unsaturated moisture flow equation with app lication to evaporation from a water table[J].Soil Science,1958, 85：228-232.

[13]MCKEE C,BUMB A.The im portance of unsaturated flow parameters in designing a hazardous waste site[C]// Hazardous Wastes and Environmental Emergencies (Hazardous Materials Control Research Institute National Conference).Houston,TX,March 1984：50-58.

(编辑 王秀玲)

Numerical Analysis of Seepage and Deformation in Unsaturated Soils

WULi-zhou,HUANGRun-qiu

(State Key Laboratory of Geo logical Hazard Prevention and Geological Environment Protection, Chengdu University of Technology,Chengdu 610069,P.R.China)

Based on one-dimensional seepage and deform ation governing equations,PDE software is used to analyze the coupled governing equations.The method is available to arbitrary functions of SWCC(soilwater characteristic curve),and it considers that both the coefficient of perm eability at saturation and the po rosity change w ith soil strain.Compared with analy tical so lution,the numerical solution show s high precision and it can effectively solve coupling problem s.It is found that coup ling effect of seepage and deformation in unsaturated soils p lays an important role in the pore-water pressure profiles,and that the coup ling effect shou ld be considered during rain fall infiltration.A t early stage of rain fall infiltration, settlement obviously increasesw ith time,and the pore-water pressure considering the coup lingmovesmore slow ly than thatw ithout considering coup ling due to positiveH.The settlement is related w ith initial porewater pressure profiles andHvalue.The coefficient of perm eability at saturation and the porosity have an effect on rainfall infiltration and steady-state seepage,but their change hasaweak influence on deformation in unsaturated soils..

unsaturated soil;coup led seepage and deformation;rainfall infiltration;numerical analysis

文献标志码：A

1674-4764(2011)03-0063-05

2010-12-22

国家自然科学基金(40902087);教育部科学技术研究重点项目(110186);教育部博士点新教师基金(20095122120007)

吴礼舟(1975-),男,副教授,博士后,主要从事非饱和土及其边坡灾害研究,(E-mail)w ulizhoucn@yahoo.com.cn