腹板嵌入式组合梁抗弯性能理论和试验研究

李国强,李 亮,李现辉,司林军

(1.同济大学a.土木工程学院;b.土木工程防灾国家重点实验室,上海 200092; 2.河南徐辉建筑工程设计事务所,郑州 450008)

腹板嵌入式组合梁抗弯性能理论和试验研究

李国强1a,1b,李 亮1a,李现辉2,司林军1a

(1.同济大学a.土木工程学院;b.土木工程防灾国家重点实验室,上海 200092; 2.河南徐辉建筑工程设计事务所,郑州 450008)

提出了一种新型腹板嵌入式钢-混凝土组合梁,并对该组合梁的整体抗弯性能和抗剪性能进行了研究。首先阐述了腹板嵌入式钢-混凝土组合梁的构成、受力特点和主要优点,然后介绍了该组合梁的抗弯承载力、钢梁与混凝土翼板之间的滑移以及挠度计算公式。通过竖向荷载作用下的静力加载试验对4个腹板嵌入式钢-混凝土组合梁试件的抗弯承载力、滑移影响及破坏特征进行了足尺试验研究,并利用有限元方法对4个试件的试验结果进行了对比,最后将理论公式得到的腹板嵌入式钢-混凝土组合梁的抗弯承载力、滑移及挠度计算结果与试验及有限元分析的结果进行比较,验证了理论公式的可靠性。研究表明,腹板嵌入式钢-混凝土组合梁具有良好的整体抗弯性能及抗剪性能,能够节约钢材。

组合梁;梯形连接件;倒T型钢梁;抗弯承载力

传统的钢-混凝土组合梁利用H型钢梁来承受 拉力,依靠混凝土翼板来承受压力,有效地发挥了钢材和混凝土的优点,在建筑工程中得到广泛应用[1-3],如图1(a)所示。由于H型钢梁上翼缘离截面中和轴较近,在正弯矩作用下应力较小,因此材料强度没有充分发挥。腹板嵌入式钢-混凝土组合梁略去了钢梁的上翼缘,用腹板顶部的梯形连接件代替栓钉,不仅减小钢材用量而且避免了焊接工序,降低了工程造价,具有显著的经济效益,如图1(b)所示。为了使腹板嵌入式组合梁在实际工程得到推广,有必要对其抗弯性能和抗剪性能进行研究。

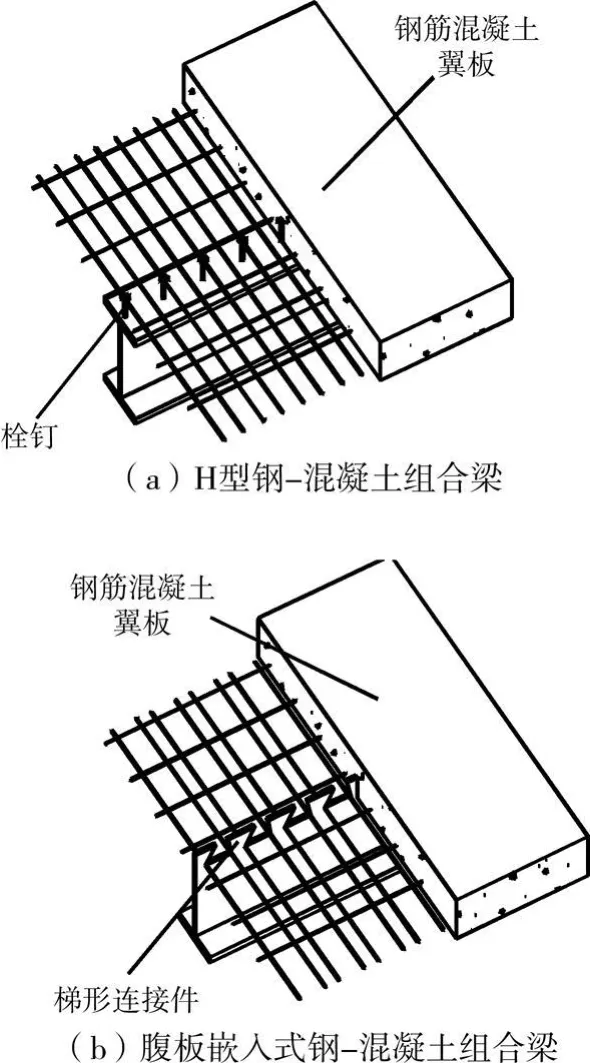
图1 钢-混凝土组合梁

梯形连接件将楼板与钢梁连为一体,对于保障混凝土楼板与钢梁协同工作具有重要意义。文献[4]对6个足尺腹板嵌入式组合梁试件连接件的抗剪性能进行了试验研究和参数分析,试验结果表明梯形连接件具有较高的抗剪承载力,易于在混凝土楼板与钢梁之间实现完全抗剪连接。文献[5]通过对6个组合梁试件的梯形连接件进行抗拔试验,研究了连接件的抗拔性能及其影响因素,试验结果表明连接件的抗拔承载力均远大于其抗剪承载力的10%,能够保证混凝土板与钢梁之间具有足够的抗拔能力。由于钢梁为倒T形截面,其侧向刚度低,稳定性较差,不利于施工阶段的受力,因此文献[6-7]提出在钢梁下翼缘上部设置垫块和施工支撑的方法,当倒T钢梁承受施工荷载时,荷载作用点下移,有利于提高钢梁的稳定性,可满足施工阶段承受施工荷载的要求。

该文首先介绍了腹板嵌入式组合梁抗弯承载力、滑移和挠度的计算公式。通过对4个足尺试件进行试验,研究了组合梁的抗弯性能、滑移效应及破坏特征,并利用有限元方法对4个试件的试验过程进行模拟。最后,将理论公式计算得到的抗弯承载力、滑移及挠度与试验和有限元分析结果进行对比,验证理论公式的可靠性。

1 腹板嵌入式组合梁抗弯及滑移计算

1.1 基本假定

采用塑性分析法计算腹板嵌入式组合梁的抗弯承载力。为此采用以下基本假定[8-10]：

1)连接件能够保证钢梁与混凝土翼板协同工作,且钢梁不会发生局部和整体失稳;

2)混凝土受压区应力均匀分布,能达到抗压设计强度,同时不考虑受拉混凝土开裂后性能;

3)钢梁的受拉区和受压区应力均匀分布,且均能达到钢材的设计强度。

1.2 抗弯承载力计算

组合梁按塑性中和轴的位置可分为2类截面：第1类截面塑性中和轴位于混凝土翼板内;第2类截面塑性中和轴位于钢梁腹板内,如图2所示。

图2 组合梁截面分类及应力分布

1)第1类截面抗弯承载力计算公式

第1类截面的塑性中和轴位于混凝土翼板内,于是：

由力矩的平衡条件可得：

由截面上力的平衡条件可得：

式中,A为钢梁的截面面积;f为钢材抗拉强度设计值为混凝土翼板的有效宽度;为混凝土翼板的厚度;fc为混凝土抗压强度设计值;M为正弯矩设计值;x为混凝土受压区高度;y为钢梁截面形心与混凝土受压区截面应力合力的距离。

2)第2类截面抗弯承载力计算公式

第类截面是塑性中和轴位于钢梁腹板内,于是：

根据截面上力的平衡条件,可得

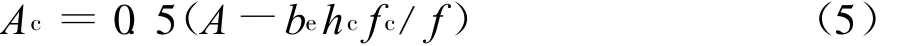
由截面上力矩的平衡条件可得

式中,Ac为钢梁受压区截面面积;y1为钢梁受拉区截面形心到混凝土翼板受压区截面形心的距离;y2为钢梁受拉区截面形心到钢梁受压区截面形心的距离。

1.3 滑移及挠度计算公式

1.3.1 滑移的计算公式 在竖向荷载作用下钢梁与混凝土翼板之间会产生剪力,并伴随着滑移发生。通过求解平衡微分方程,得到简支腹板嵌入式组合梁交界面上滑移的微分方程为[8,12]： 2

式中,q为均布荷载;x为滑移计算位置相距梁左端的长度;l为简支梁的跨度。

在对称集中荷载作用下,滑移沿梁长的分布函数为：

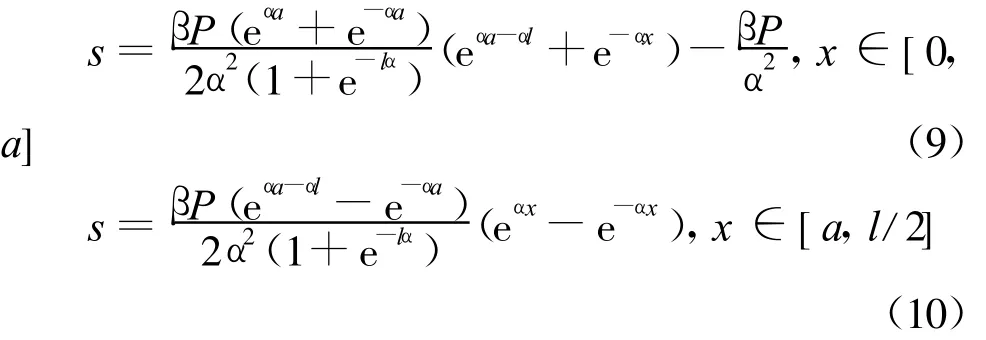
式中,P为集中荷载;a为竖向荷载作用点相距梁左端的长度。

1.3.2 考虑滑移效应时组合梁挠度计算公式 根据叠加原理钢-混凝土组合梁总挠度为：

式中,δe为根据弹性换算截面法得到的挠度;Δδ为滑移效应引起的附加挠度。

在均布荷载下由滑移效应引起的简支梁附加挠度为[11,13]：

在两点集中荷载下由滑移效应引起的简支梁附加挠度为：

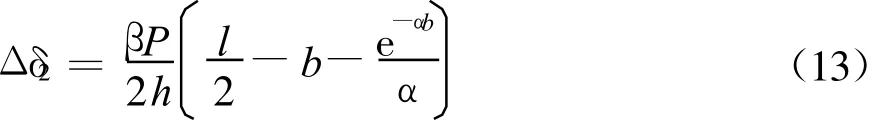
式中,b为集中荷载到跨中的距离。

2 腹板嵌入式组合梁抗弯性能试验研究

2.1 试件介绍

设计了4根腹板嵌入式组合梁试件来研究竖向荷载作用下组合梁的抗弯性能、滑移效应和破坏机理,同时研究混凝土强度、组合梁截面高度、梯形连接件尺寸和横向配筋率等参数的影响,试件尺寸如图3所示,具体参数详见表1。

图3 试件ECB-1,ECB-2(ECB-3,ECB-4)尺寸详图

表1 试件主要参数表

钢梁采用Q235级钢,由材性试验得到钢材的屈服强度为300 MPa,弹性模量为2×105MPa;混凝土抗压强度根据边长为150 mm的立方体试件标准试验方法测得,C20的抗压强度为 24.47 N/mm2,C30的抗压强度为30.86 N/mm2。

2.2 加载方案

试验在同济大学结构试验室完成。所有组合梁试件两端均采用铰接,其中固定铰接支座用固定钢棒来实现,而滑动铰接支座采用可滑动钢棒来实现。通过2根钢梁(型号为I20a)将竖向荷载均匀地传递到混凝土翼板上,如图4所示。

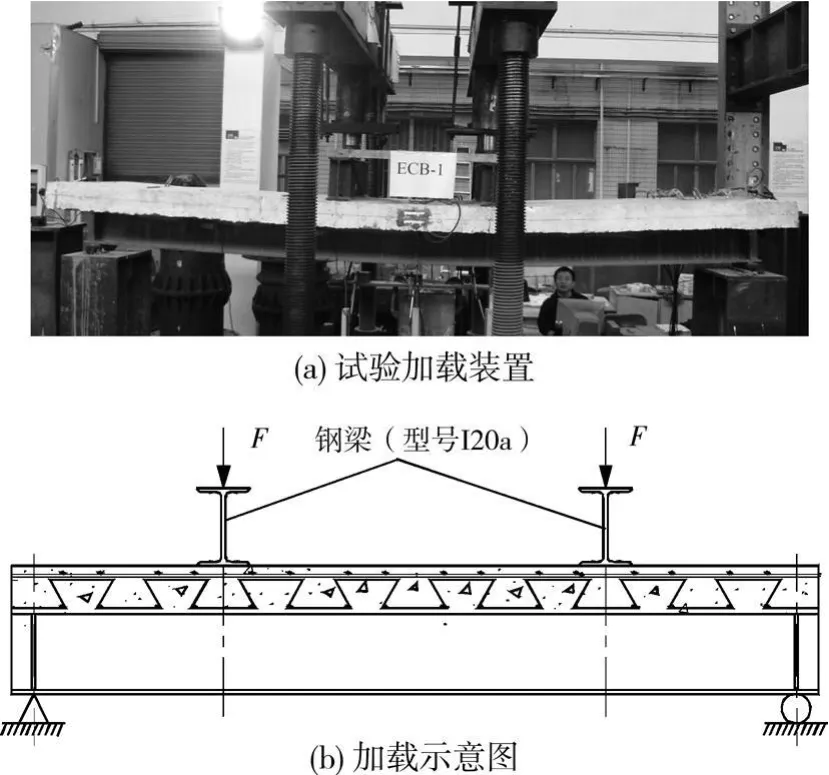
图4 试件加载方案

加载方案是先加载0.2(为预计的极限承载力),并保持一段时间(目的是为了观察位移计和应变计读数是否正常),然后完全卸载后再重新单调加载至试件破坏。

2.3 测量方案

4个试件测量方案完全相同。每个试件设置10个位移计对组合梁不同部位的位移和滑移进行量测：1)位移计d1—d3是为了测量组合梁跨中和加载点处挠度;2)位移计d4—d7是为了对组合梁两端侧向位移及支座沉降进行量测;3)在半跨均匀布置的位移计d8—d10以测量混凝土翼板和倒 T形钢梁之间的滑移,如图5(a)所示。

每个试件上设置17个应变片对组合梁对称轴上不同部位的应变进行了量测：1)在混凝土翼板侧面、钢梁腹板侧面以及翼缘底面共布置8个应变片来测量跨中不同梁高部位的应变,如图6(a)所示; 2)在混凝土翼板顶面沿对称轴均匀布置9个应变片来测量混凝土翼板的压应变,如图6(b)所示。

图5 组合梁上位移计布置

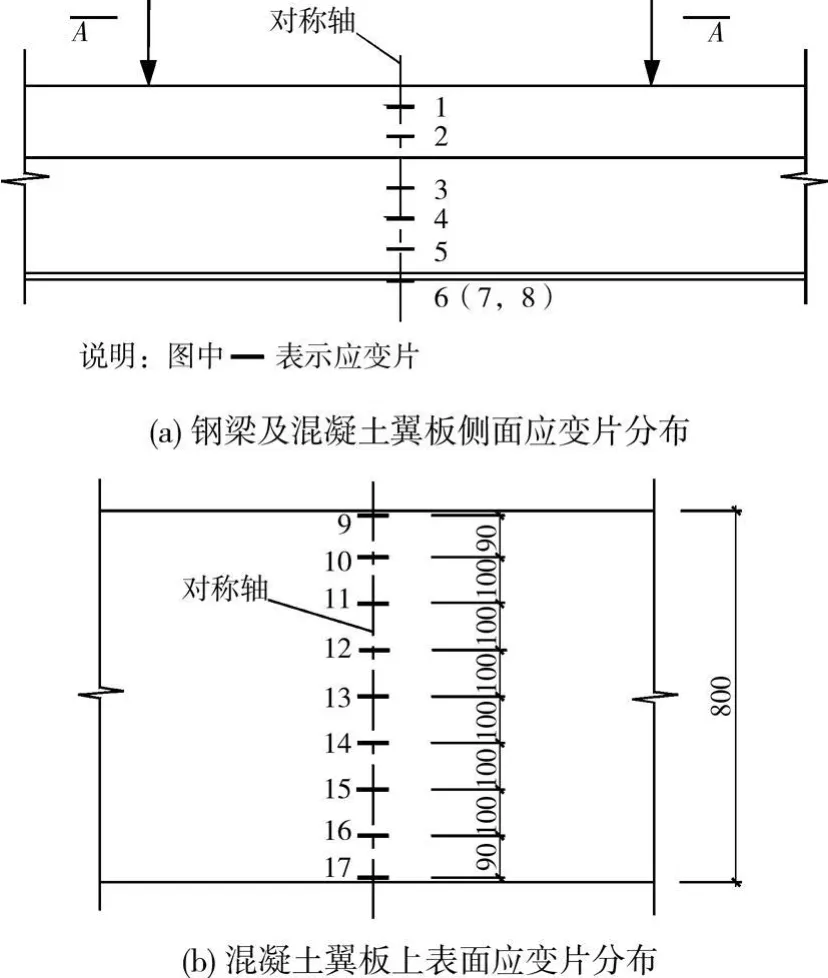
图6 组合梁上应变片布置示意图

2.4 试验现象及破坏特征

在垂直于钢梁方向,通过对4个试件的数据进行汇总,可知当荷载低于0.2～0.4Pu时,混凝土翼板没有出现裂缝,整个构件处于弹性状态;当荷载达到0.6～0.7Pu时,在混凝土翼板侧面加载梁的位置分别出现一条竖向裂缝,如图7(a)所示;当荷载达到0.7～0.8Pu时,加载梁之间的纯弯段混凝土翼板侧面出现多道竖向裂缝且分布均匀,如图7(b)所示;当荷载达到0.8～0.9Pu时,混凝土翼板中的裂缝宽度进一步增大,混凝土翼板下部出现开裂和剥落现象,且倒T形钢梁下翼缘钢材应变达到屈服值,如图7(c)所示;当荷载达到极限荷载时,加载梁处混凝土裂缝宽度增大并相互贯通,混凝土严重剥落,组合梁弯曲变形明显并达到极限状态,如图7 (d)所示。

图7 混凝土板裂缝发展过程(垂直于钢梁轴线方向)

在沿着钢梁轴线方向,当荷载低于0.2～0.4Pu时,钢梁和混凝土翼板之间没有明显的滑移;当荷载达到0.4～0.6Pu时,混凝土翼板和钢梁之间检测到微小的滑移,但沿着钢梁轴线方向在混凝土翼板上尚未观测到裂缝;当荷载达到0.7～0.8Pu时,钢梁和混凝土翼板之间发生明显滑移,同时在混凝土翼板上沿着梯形连接件的方向出现裂缝,如图8(a)所示;当荷载达到极限荷载时,混凝土翼板上的裂缝开裂非常明显,且裂缝致使混凝土翼板局部部位出现隆起现象而破坏严重,如图8(b)所示。

图8 混凝土板裂缝发展过程(沿钢梁轴线方向)

2.5 试验结果及分析

对试验数据进行整理,得到4根腹板嵌入式组合梁的荷载-跨中挠度关系曲线,如图9(a)所示。当荷载低于0.6～0.7Pu时,荷载-跨中挠度曲线都呈线性发展,构件处于弹性状态;当荷载为0.8～0.9时,组合梁的刚度明显下降,荷载-跨中挠度关系曲线的非线性特征越来越显著,构件处于弹塑性阶段;当荷载达到大约0.95Pu时,荷载基本不变而挠度迅速增大,荷载-跨中挠度曲线接近水平,组合梁的挠度发展迅速,试件很快发生破坏。

将位移计测得的滑移数据进行比较,可知位移计d9测得的滑移最大,考虑到加载梁宽度的影响,可确定最大滑移发生在集中荷载作用点处。各试件荷载-最大滑移曲线如图9(b)所示,当荷载低于0.6～0.7时,基本没有滑移;当荷载为0.8～0.9时,滑移迅速增大;当荷载达到大约0.95时,荷载基本不变而滑移迅速增大,荷载-滑移曲线接近水平。

分析表明,试件ECB-1和ECB-2(ECB-3和ECB-4)除了混凝土强度等级不同以外,其它参数完全一致,而其荷载-跨中挠度曲线和荷载-最大滑移曲线基本一致。因此对于中和轴位于混凝土板内的腹板嵌入式钢-混凝土组合梁,混凝土强度等级对构件的承载力和延性影响不显著。

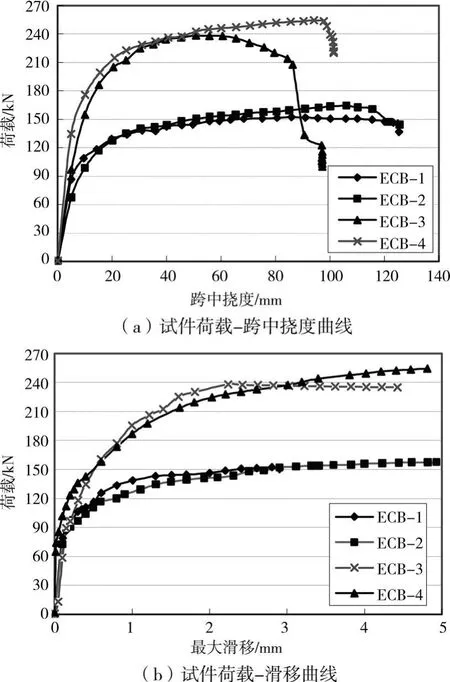
图9 嵌入式组合梁试验曲线

3 抗弯性能有限元分析

3.1 模型介绍

为了将有限元分析结果与试验结果进行对比,对4个试验试件进行了竖向荷载作用下的有限元分析,划分单元后的有限元模型如图10所示,具体介绍如下：

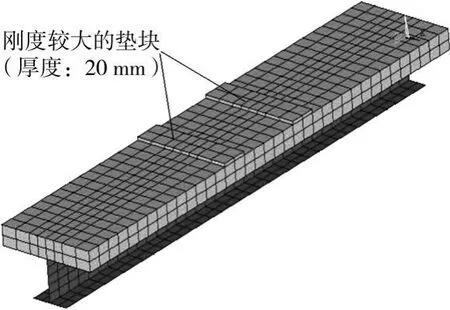
图10 单元划分后的组合梁有限元模型

1)钢梁采用4节点三维shell181壳单元来模拟,该单元能考虑钢材塑性和大变形的影响。

2)混凝土翼板采用8节点solid65实体单元模拟,该单元通过定义混凝土材料的W illam&W arnke 5参数破坏准则和弹塑性本构关系来考虑混凝土开裂、压碎、塑性变形和蠕变影响[14],从而得到混凝土的开裂情况;钢筋采用弥散式配筋模型,通过定义配筋率来模拟分散在混凝土中的钢筋网。

3)混凝土翼板与钢梁之间的连接滑移效应采用非线性弹簧单元Combin39来模拟,弹簧单元的力-变形曲线根据文献[4]的推出试验结果得到。

钢材采用材性试验的数据,σ-ε关系取双线性随动强化模型;混凝土采用C20和C30,由《混凝土结构设计规范》得到抗拉强度分别1.68 MPa和2.57 MPa,σ-ε关系采用E.Hognestad模型。

3.2 分析结果

通过对腹板嵌入式组合梁的有限元模型进行分析,得到了在竖向荷载作用下混凝土楼板的纵向裂缝分布情况,如图12所示。将有限元结果与试验结果进行对比,可知在竖向荷载作用下有限元模型中混凝土翼板顶部裂缝走向(如图11)与试验得到的裂缝走向(如图8)符合良好。

图11 有限元模型(混凝土纵向裂缝分布)

将有限元分析得到的组合梁荷载-跨中挠度曲线与试验结果进行对比,可知有限元分析得到的构件初始刚度与试验结果符合较好,有限元分析得到的极限承载力略高于试验结果,基本上符合较好,如图12所示。同时,有限元分析也表明,腹板嵌入式组合梁具有较高的抗弯承载能力和良好的延性性能。

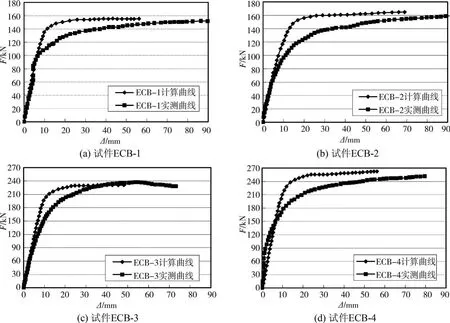
图12 有限元分析与试验研究结果对比(荷载-挠度曲线)

4 各种结果对比

4.1 抗弯承载力公式验证

为了验证腹板嵌入式钢-混凝土组合梁抗弯承载力计算公式的可靠性,将理论公式得到的抗弯承载力与试验值和有限元分析值进行对比,可知理论公式计算得到的抗弯承载力与试验和有限元方法得到的抗弯承载力吻合较好,如表2所示。因此,在工程实际中利用塑性计算方法估计腹板嵌入式钢-混凝土组合梁的抗弯承载力是可靠的。

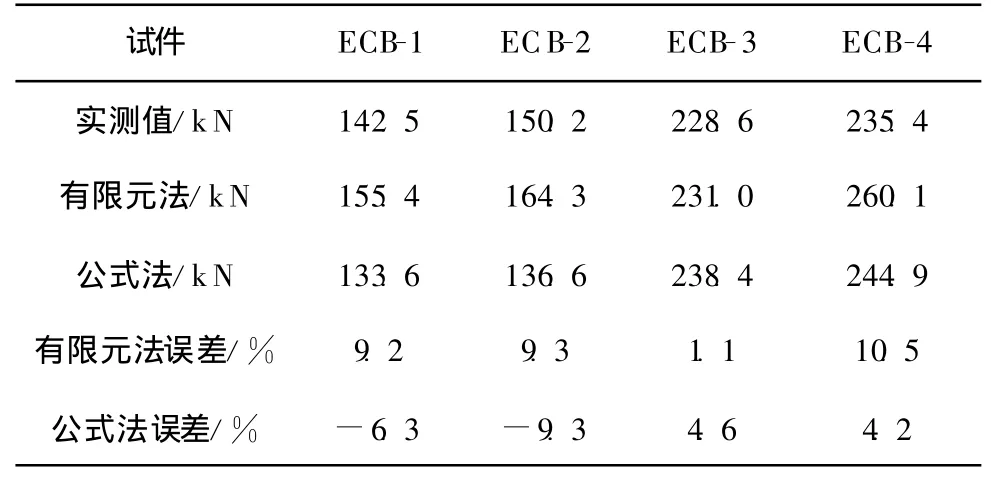
表2 不同方法所得抗弯承载力比较

4.2 滑移及其对挠度的影响

在正常使用状态时,将竖向荷载为0.6Pu时腹板嵌入组合梁滑移的测量值与理论公式的计算值进行对比,可知理论公式得到的滑移大于实测滑移,见表3。

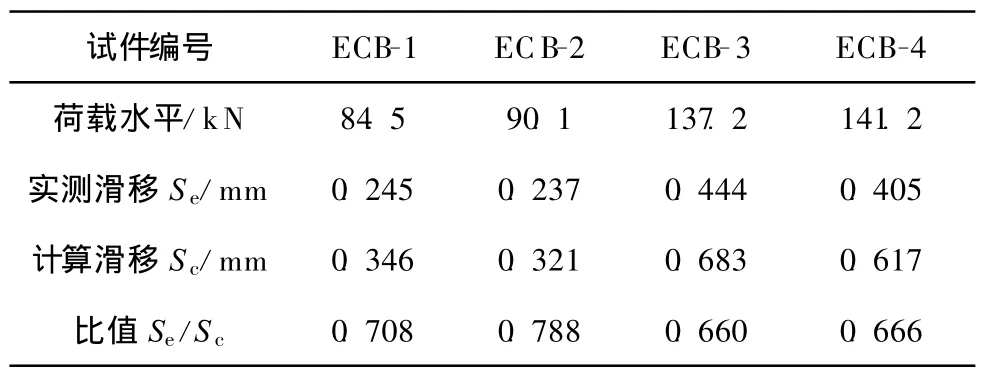
表3 滑移实测值与计算值的比较

根据提出的挠度计算公式来研究滑移效应对挠度的影响,对比发现不考虑滑移影响时挠度和考虑滑移影响时挠度比值的平均值为0.958,可见不考虑滑移影响所带来的挠度误差小于5%,满足工程精度要求,如表4所示。因此计算腹板嵌入式组合梁在正常使用状态下的挠度时可忽略滑移效应的影响。

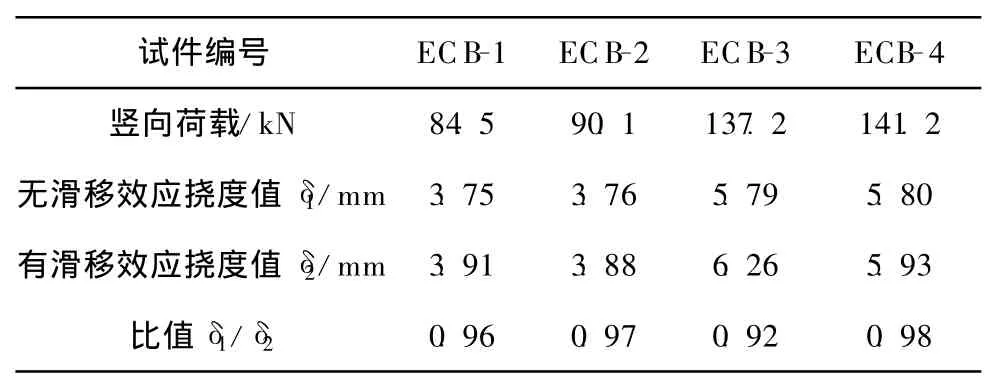
表4 考虑和不考虑滑移效应时的挠度的比较

5 结 论

通过对倒T型腹板嵌入式组合梁的抗弯性能、滑移效应和破坏特征进行理论分析、试验及有限元研究,可以得出以下结论：

1)腹板嵌入式组合梁不仅能够节约钢材具有显著的经济效益,而且具有较高的抗弯承载力和良好的延性,应用前景非常广泛。

2)塑性理论公式得到的组合梁抗弯承载力与试验和有限元方法得到的计算结果符合良好,该理论公式可用于工程实际。

3)由滑移效应引起的腹板嵌入式组合梁附加挠度很小,计算正常使用状态下组合梁的挠度可忽略滑移效的影响。

[1]NEWMARK N M,SIESSC P,V IEST IM.Test and analysis of composite beams with incomplete interaction [J].Experimental Stress Analysis,1951,9(6)：896-901.

[2]H IGGINS C,MITCHELL H.Behavior of com posite bridge decks with alternative shear connectors[J]. Journal of Bridge Engineer,2001,6(1)：17-22.

[3]LIGUO-QIANG,LIXIAN-HUI.Study on a novel steelconcrete composite beam[C]//ICASS′09/IJSSD/IStructE Asia-Pacific Forum Sixth International Con ference on Advances in Steel Structures.2009.

[4]李现辉,李国强.腹板嵌入式组合梁中抗剪连接件推出试验[J].建筑结构学报,2009.30(4)：78-84.

LI XIAN-HUI,LI GUO-QIANG.Push-out experimental study on shear connectors in embedded compositebeamswith notched web[J].Journal of Building Structures,2009.30 (4)：78-84.

[5]李现辉,李国强.腹板嵌入式组合梁中抗剪连接件拔出试验[J].建筑科学与工程学报,2009,26(1)：43-48.

LI XIAN-HUI,LI GUO-QIANG.Pull-out experimental study on shear connector in embedded composite beamswith notched web[J].Journal of Architecture and Civil Engineering,2009,26(1)：43-48.

[6]LI XIAN-HU I,LI GUO-QIANG.Study on the behavior of embedded steel-concrete composite beams with notched web during construction stage[C]//9th International Conference on Steel Concrete Com posite and Hybrid Structures,Leeds,UK,2009.

[7]李国强,李现辉,张哲.腹板嵌入式钢-混凝土组合梁施工阶段受力性能研究[J].土木工程学报,2009,42(12)：61-68.

LI GUO-QIANG,LI XIAN-HU I,ZHANG ZH E. Mechanical characteristics of steel-concrete composite beams with embedded w ebs during construction[J]. China Civil Engineering Journal,2009,42(12)：61-68.

[8]聂建国,樊建生.广义组合结构及其发展展望[J].建筑结构学报,2006,27(6)：1-8.

NIE JIAN-GUO,FAN JIAN-SHENG.The developmentand p rospectof the generalized composite structure[J].Journal of Building Structures,2006 27(6)：1-8.

[9]GB 50017-2003钢结构设计规范[S].北京：中国计划出版社,2003.

[10]聂建国,沈聚敏,余志武.考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J].土木工程学报,1995, 28(6)：11-17.

NIE JIAN-GUO,SHEN JU-MIN,YU ZHI-WU.A reduced rigidity method for calculating deformation of composite steel-concrete beam s[J].Journalof Building Structures,1995,28(6)：11-17.

[11]聂建国.钢-混凝土组合梁结构[M].北京：科学出版社2005.

[12]CRISINEL M.Partial-interaction analysis of com posite beams with profiled sheeting and non-welded shear connectors[J].Journalof Construction Steel Research, 1990,15：65-98.

[13]王连广.钢与混凝土组合结构理论与计算[M].北京：科学出版社,2005.

[14]陆新征,江见鲸.利用ANSYSSolid 65单元分析复杂应力条件下的混凝土结构[J].建筑结构,2003,33(6),22-24

LU XIN-ZH ENG,JIANG JIAN-JING.Analysis for concrete structure under comp lex stress condition w ith Solid 65 FEA Element of ANSYS[J].Building Structure,2003,33(6),22-24.

(编辑 胡英奎)

Theoretical and Experimental Analysis of Bending Behavior of Com posite Beam w ith Notched Web

LIGuo-qiang1a,1b,LILiang1a,LIXian-hui2,SILin-jun1a

(1a.College of Civil Engineering;1b.State Key Laboratory for Disaster Reduction in Civil Engineering,Tongji University, Shanghai200092,P.R.China;2 Henan Sunrise A rchitectural Design Institute,Zhengzhou 450008,P.R.China)

A new kind of steel-concrete com posite beam w ith notched web is p roposed,and the bend and shear behaviors of this com posite beam are investigated.First of all,the constitution,bearing characteristics and merits of the steel-concrete com posite beam with notched web are introduced;then,a group of formulas about the bending capacity,slip between the steelbeam and the concrete flange,and the deflection are introduced;after that,the bending behavior,slip effect and bearing characteristic of the steel-concrete composite beam w ith notched web are studied on 4 specim ens,which are tested by applying tw o concreted vertical loads on the top of concrete flange.A nd the finite element model is adop ted to analyze the results of the 4 specimens;finally,the reliabilities of the formulasareverified by comparing the resu lts of theoretical formu las,the resu lts of tests and that of finite elem ent analysis.Study show s that the bend behavior and shear behavior are fine,and the popularization of thisnew kind of compositebeam which can be broadly used in building engineering w ill save the consump tion of steel.

com posite beams and girders;notched web;inverted T-shaped steel beam;bending capacity

TU375.1

A

1674-4764(2011)03-0001-07

2010-10-16

国家科技支撑计划项目(2006BAJ01B02)

李国强(1963-),男,教授,博士生导师,主要从事多高层钢结构及钢结构抗火性能研究,(E-mail)gq li@mail. tong ji.edu.cn。