PC连续箱梁合龙束横向效应

项贻强,唐国斌,朱汉华,晁春峰

(1.浙江大学土木工程系,杭州 310058;2.浙江省公路管理局,杭州 310058)

PC连续箱梁合龙束横向效应

项贻强1,唐国斌1,朱汉华2,晁春峰1

(1.浙江大学土木工程系,杭州 310058;2.浙江省公路管理局,杭州 310058)

PC连续箱梁合龙束张拉不仅使底板纵向受压,同时在横向产生附加效应;以某跨海大桥为例,对底板合龙束作用机理进行探讨,并通过精细有限元模型,对施工过程中合龙束的横向效应进行分析和参数研究;结果表明,合龙束张拉过程中底板横向应力处于动态变化过程,其横向效应远大于恒载和其它预应力作用结果,同时,合龙束的横向效应对底板的线形、厚度及孔道保护层较为敏感;最后,基于横向框架法,通过引入预应力效应简化系数和孔道修正系数,提出合龙束横向效应的简化计算方法。

桥梁工程;箱梁;合龙束;横向效应;参数分析

PC连续箱梁(刚构)桥底板合龙束的布置是为了平衡活载作用弯矩,但在其张拉过程,由于箱梁的空间作用在底板横向产生附加效应。但目前桥梁设计仍主要依据平面分析结果,这种方法难以计算合龙束张拉过程的附加效应。尤其是随着大吨位预应力束群锚体系的应用[1],合龙束的附加效应更趋明显。如果设计未加以考虑,可能导致施工过程中底板开裂,甚至崩裂。

近年来,合龙束横向效应导致的箱梁开裂问题时常见诸于国内外论文中。Podolny[2]、Chatelain等[3]较早地对合龙束引起的开裂进行定性分析。Breen等[4]对箱梁底板合龙束及构造钢筋的布置进行研究,其结论为美国规范所引用[5]。Moon DoYoung等[6]利用板壳元分析节段施工箱梁底板开裂原因。Jiang Haibo[7]采用局部模型对这类问题进行研究。郭丰哲等[8]也采用这种方法分析孔道偏差对横向效应的影响。王蒂等[9]]从剪切变形、泊松效应及压区失稳等角度探讨合龙束的横向效应。总体而言,这些研究加深了对合龙束横向效应的认识。但以上研究多采用局部模型,难以全面反映合龙束的空间效应,同时也缺乏对施工过程的考虑。

以某跨海大桥北引桥底板开裂事故为例,首先对合龙束作用的机理进行分析,并建立精细有限元模型,对合龙束的附加效应进行分析,在此基础上,探讨了箱梁底板线形、孔道保护层厚度、底板厚度和横向配筋的影响,并提出合龙束附加效应简化的计算方法。

1 合龙束作用机理

变截面箱梁的合龙束通常为曲线预应力束,曲线预应力的形成上与直线有所不同。直线束主要通过锚头挤压构件端部,借此向内传递压力,而曲线预应力束则是通过预应力钢绞线张拉变形挤压孔道壁,使混凝土形成预压应力。

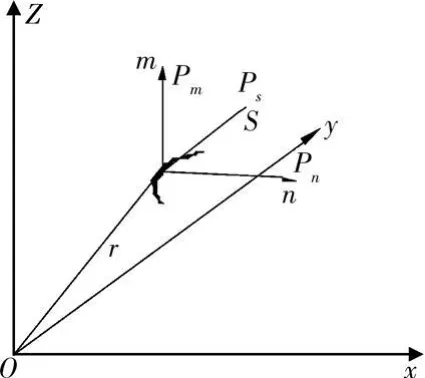
图1 曲线预应力束的作用

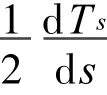
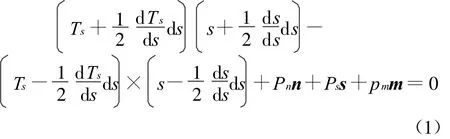
由d s/d s=kn,式中k为s点的曲率,则：

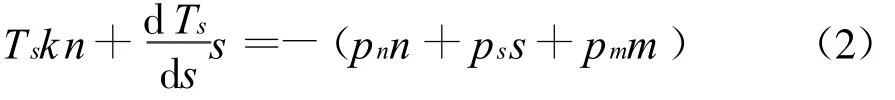
写成标量形式：

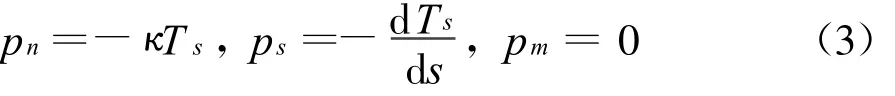
根据上述曲线预应力作用机理,合龙束在张拉和锚固过程中对底板将产生两种作用,即预应力钢筋对孔道壁的径向挤压力和切向拖曳力。对预应力混凝土箱梁而言,预应力束与孔道壁的摩擦系数一般位于0.15～0.30之间,三维有限元分析表明,切向拖曳力对底板混凝土应力状态的影响甚微,其数值不超过由径向力所引起应力的5%,因而可忽略。

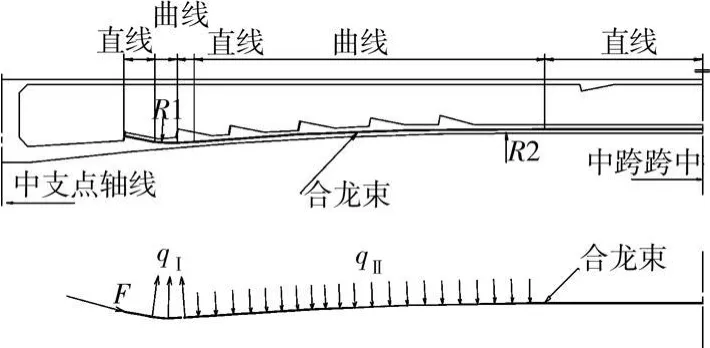
图2 典型合龙束及其等效荷载

图2为某连续箱梁合龙束示意图,其等效荷载包括张拉力F、向上径向力qI及向下径向力qII,如图5所示,其中F为集中荷载,qI作用范围较小为局部荷载,qII为分布荷载。

2 空间分析

2.1 工程实例

某跨海大桥北引桥其中一联为(50+80+50)m三跨预应力混凝土变高度连续箱梁,中跨支点和跨中截面特征如图3所示,底板线形采用半径为256.806 m的圆曲线。箱梁采用三向预应力体系,其中纵向按全预应力结构设计,顶板横向按部分预应力结构设计,底板横向按钢筋混凝土结构设计。

该桥采用悬臂挂篮现浇施工,纵向共划分9个节段,如图4所示。底板合龙束(N22～N17)采用12-7φ5钢绞线,张拉控制力2 344 kN,分布于1～6号节段。按正常工序进行中跨合龙后,依次张拉1 -6号块合龙束,张拉至4号块N19束时,4、5和7号块底板下缘均出现裂缝,其中纵向裂缝最大长度约2.3m,随后5号和7号块开裂处混凝土崩裂,崩裂面积分别约2.5m2和2.0 m2。

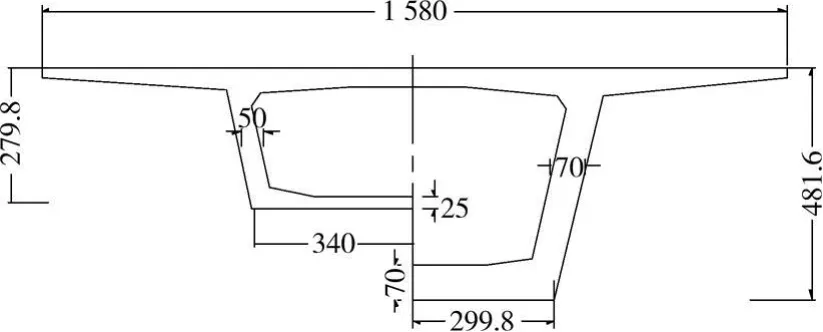
图3 箱梁中支点和跨中截面特征

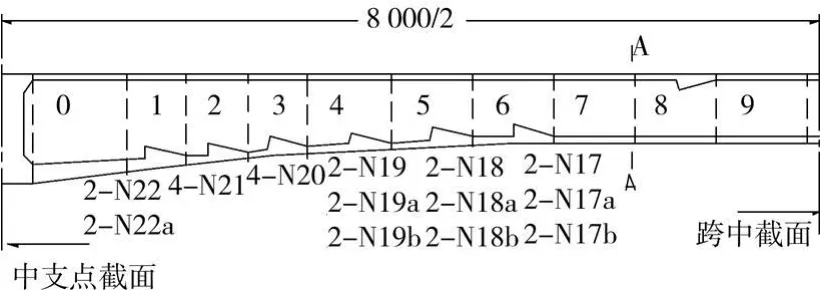
图4 箱梁施工节段和底板合龙束布置

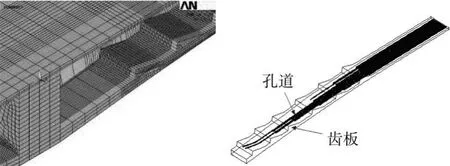
图5 计算模型

根据箱梁开裂特征,初步判断为合龙束的横向效应所致,为此采用空间有限元对施工过程中合龙束横向效应进行分析。其中,混凝土采用实体单元模拟,为便于网格划分将合龙束圆形孔道(直径76 mm)等效为矩形,有限元离散模型如图5所示。普通钢筋采用杆单元模拟,除中跨底板合龙束外,其它预应力束也采用杆单元模拟。中跨底板合龙束预应力的施加采用等效荷载模拟,其它采用等效降温法。根据箱梁的施工过程将计算划分为19个荷载步,其中1-13步分别为各节段悬臂施工、体系转化及边、中跨合龙过程,14-19步为1-6号块合龙束的张拉过程。

2.2 结果分析

2.2.1 空间应力分布状况

图6绘出4号块合龙束张拉后中跨底板的应力状况,图中A、B和C3处主拉应力均已超过C50混凝土抗拉强度标准值,与实际工程开裂位置一致。

图7绘出A、B、C3处底板下缘横向应力分布沿横向分布情况。由图可知,A处底板横向应力分布较为复杂,由于A处靠近4号块齿板,直接作用此处的荷载包括N22～N20束向下径向力qII和N19束向上径向力qI,此外N 19束集中荷载F对A处应力也有较大的影响;而在B、C两处由于直接作用在此处的荷载为N22～N 19束向下径向力qII,横向应力分布规律较为类似。

图6 合龙束张拉后箱梁主拉应力云图

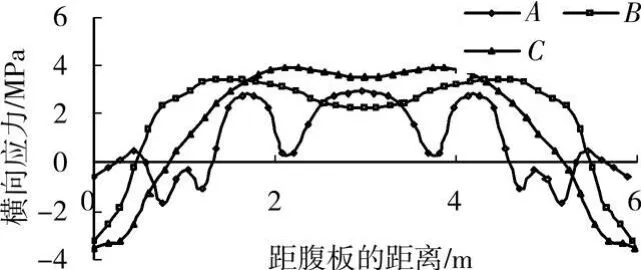
图7 A、B、C处底板下缘横向应力沿横向分布

2.2.2 施工过程的影响

图8绘出不同施工阶段底板中心线处纵向应力的变化情况：

1)合龙束张拉前,底板横向应力由结构恒载和顶板预应力效应引起,此时底板中心下缘横向受压区分布在支座及1-3号块齿板下缘,其余为受拉区;

2)随着1号块(N 22束)张拉,0-1号块底板拉应力峰值减小,压应力峰值增大,2-9号块拉、压应力均增大,如图8(a)所示;

3)随着2号块(N 21束)张拉,0-2号块底板拉应力峰值减小,压应力峰值增大,3-9号拉、压应力峰值增大,如图8(b)所示;

4)随着3号块(N20束)的张拉,0-1号块底板应力变化不大,2-3号拉应力峰值减小,压应力峰值增大,4-9号块拉应力峰值增大,如图8(c)所示;

5)随着4号块(N19束)的张拉,0-2号块底板应力变化不大,3-4号拉应力峰值减小,压应力峰值增大,4-9号块拉应力峰值增大,如图8(d)所示。

图8 不同施工阶段箱梁底板中心线处横向应力

综上所述,随着合龙束的张拉,底板横向应力处于动态变化过程,任一节段合龙束的张拉使其前节段的横向拉应力减小,其后节段的横向拉应力增大。而跨中附近承担径向力的节段,在合龙束张拉过程中,横向效应持续增大,并远大于恒载和其它预应力作用结果。

3 影响因素分析

3.1 底板线形

变截面箱梁底板的线形有圆弧线、二次抛物线、多次抛物线等,以上述计算模型为基础,假定箱梁底板线形依次按照1.6次、1.8次、2次、2.3次和2.5次抛物线变化,图9绘出底板最大横向拉应力与线形的关系。由图可知,抛物线幂次越低,底板横向拉应力越大,张拉过程中底板开裂的风险也越大。对合龙束张拉过程底板开裂的箱梁调查发现[9],其底板通常采用1.5～1.8次的抛物线,而早期设计采用高次抛物线的箱梁则开裂较少。

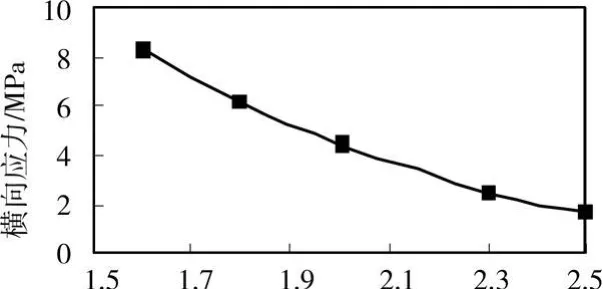
图9 底板横向最大拉应力与线形的关系曲线

3.2 底板厚度

假定底板厚度由20 cm逐渐变厚至40 cm,图10绘出底板最大横向拉应力与底板厚度的关系曲线。由图可知,当底板厚度由25 cm增大至40 cm时,最大横向拉应力减小44.1%。《桥规》[10]对箱梁底板厚度的设计没有明确规定,中国2000年以前修建的箱梁,底板最小厚度通常为32 cm。近年来,随着箱梁优化设计和高强混凝土的推广应用,底板最小厚度通常采用25 cm,这也导致合龙束横向效应更加明显。

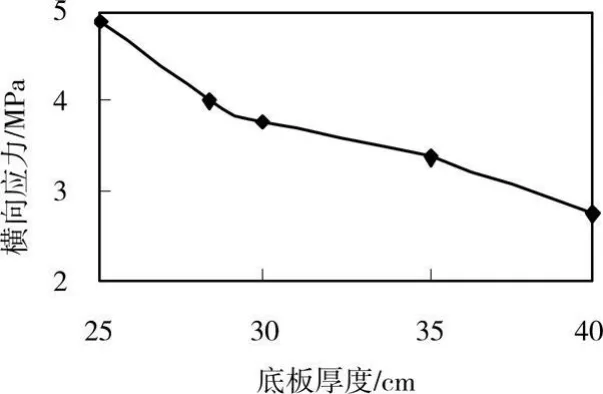
图10 底板横向最大拉应力与厚度的关系曲线

3.3 底板横向配筋

预应力混凝土箱梁底板横向通常按钢筋混凝土结构设计,为研究横向配筋对底板开裂的影响,假定配筋率分别增大和减小至原设计配筋率的1.5倍和0.5倍。图11绘出底板最大横向拉应力与配筋率的关系。当横向配筋率增大或减小50%,横向拉应力减小或增大10%,由此可见,横向配筋对横向应力的的影响较小。

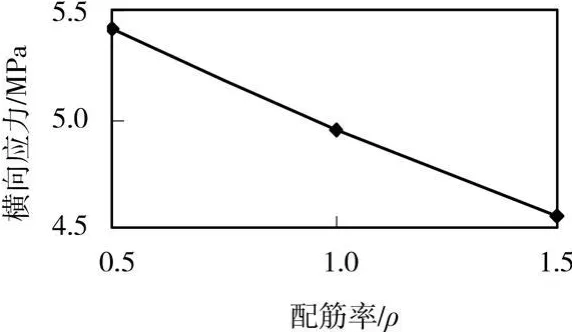
图11 底板横向最大拉应力与横向配筋率的关系曲线

3.4 孔道保护层厚度

假定合龙束孔道保护层厚度由4 cm逐渐增大至15 cm,图12绘出底板最大横向拉应力与保护层厚度的关系。由图可知,随着保护层厚度增大,最大横向拉应力逐渐减小,但当保护层厚度大于10 cm (约0.4 h,h为底板厚度)时,其影响已不明显。

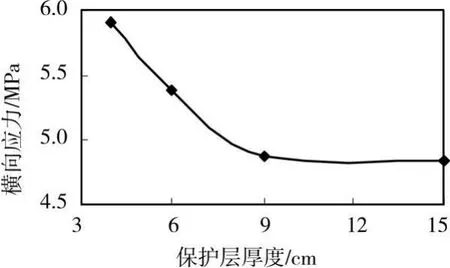
图12 底板横向拉应力与保护层厚度关系曲线

对该文箱梁,其孔道保护层厚度8.6 cm,如果施工误差±4 cm,横向最大拉应力则可能增大20%。此外,当保护层厚度较小时,底板可能出现混凝土局部崩出破坏,如图13所示。

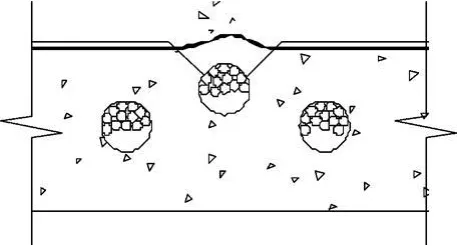
图13 合龙束张拉导致底板混凝土崩出

忽略底板弯曲效应的影响,按理想刚塑性模型来考虑,不考虑普通钢筋的贡献,假定破坏面为一45°平面,该平面上拉应力达到混凝土抗拉强度时,即发生崩裂。设孔道直径为d,保护层厚度为c,于是达到极限状态时的径向力：

4 合龙束横向效应计算

目前,中国现行桥梁设计规范(JGJ D62-2004)对箱梁底板合龙束横向效应的计算未做任何说明[10],美国规范要求验算曲线束的最小半径和孔道的间距,同时对变截面箱梁底板构造钢筋的配置做出详细规定[5],但这些规定主要防止曲线束崩出。为便于设计运用,提出合龙束横向效应的简化算法。参照已有箱梁横向分析方法,采用横向框架法(SFA)进行计算[11],计算简图如图14所示,则施工阶段底板的横向应力为：

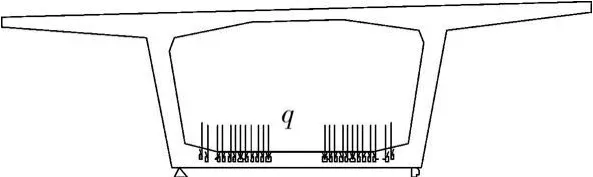
图14 径向力横向效应计算简图

恒载引起的横向应力可采用横向框架法直接计算,合龙束张拉引起的横向应力根据下式计算：

图15 不同力素引起的底板下缘横向应力分布

由于合龙束孔道的影响,孔道对截面有一定的削弱,为此引入孔道影响系数α2,根据文献[12]的计算结果,近似取α2=1.05,因而合龙束张拉阶段底板横向应力为：

其中径向力qII可按下式计算：

式中,p为张拉控制力,R为底板圆曲线半径,当为其它曲线类型时,可近似按下式计算：

式中,f和l分别为底板曲线的矢高和弦长。

5 结 论

通过对PC连续箱梁合龙束横向效应分析及参数研究,可以得出以下结论：

1)合龙束的预应力效应不仅使箱梁顺桥向受压,在张拉过程中的附加效应,使底板横向产生较大的附加弯矩,可能导致底板开裂,随着所有合龙束的张拉,跨中附近承担径向力的节段,横向效应持续增大,并远大于恒载和其它预应力作用结果。

2)合龙束的横向效应对底板线形、厚度及孔道保护层较为敏感,而底板横向配筋对横向应力的影响不大。

3)基于横向框架法,引入预应力效应简化系数和孔道修正系数,提出合龙束横向效应的简化计算方法供设计应用。

[1]杨转运,张亮亮,刘会.薄壁箱梁大吨位预压力锚固区局部承压[J].重庆大学学报：自然科学版,2007,30 (6)：114-120.

YANG ZHUAN-YUN,ZHANG LIANG-LIANG,LIU HUI.Partial pressure prob1em aboutcontinuous rigid frame bridge anchorage zone of thin concrete box girder webs carrying large tonnage[J].Journal of Chongqing University：Natural science Edition,2007,30(6)：114-120.

[2]PODOLNY,WALTER J R.The cause of cracking in post-tensioned concrete box girder bridges and retrofit p rocedures[J].Pci Journal,1985,30(2)：82-139.

[3]CHATELA IN J,GODART B,DUCHENE J L. Detection, diagnosis, and monitoring of cracked p restressed concretebridges[C]//Bridge Evaluation and Rehabilitations, 145-159. 1990 Kluw er Academ ic Pub lishers.

[4]BREEN J E,S KASH IMA.Verification of load distribution and strength of segmental post-tensioned concrete bridges[J].Engineering Structures,1991：13 (2)：113-127.

[5]AASH TO,AASH TO LRFD.Bridge design specifications [M].3rd ED.Washington,D.C,2004.

[6]MOON DO-YOUNG,SIMJONG-SUNG,OH HONGSEOB.Practical crack control during the construction of precast segmental box girder bridges[J].Computers and Structures,2005,83：2584-2593

[7]JIANG HA IBO.The cause analysis of cracks on key segment of box girder of fuli-taoyuan bridge[C]// International Conference on T ransportation Engineering 2007.Washington：ASCE,2007：807-813.

[8]郭丰哲,钱永久,李贞新.预应力混凝土连续刚构桥合龙段底板崩裂原因分析[J].公路交通科技,2005,22 (10)：68-70.

GUO FENG-ZHE,QIAN YONG-JIU,LI ZHEN-XIN. Analysis of breaking of bottom plate in continuous prestressed concrete rigid frame bridge[J].Journalof H igh Way and Transportation Research and Development,2005, 22(10)：68-70.

[9]王蒂,庞志华.预应力箱梁底板混凝土崩裂成因分析[J].混凝土,2008,(11)：43-46,61.

WANG DI,PANG ZH I-HUA.Causes of bursting on bottom plate of p restressed concrete box beam bridge [J].Concrete,2008,(11)：43-46,61.

[10]JGJD62-2004.公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[11]BABU KURIAN,DEVDAS MENON.Correction of errors in simpliyed transverse bending analysis of concrete box-girder bridges[J].Journal of Bridge Engineering,ASCE.2005,10(6)：650-657.

[12]浙江省公路管理局,浙江大学.预应力混凝土连续箱梁桥底板开裂与防治措施研究[R].2009.

(编辑 胡 玲)

Transverse Effect of Bottom Continuity Tendons in Continuous PC Box Girder

XIANGYi-qiang1,TANGGuo-bin1,ZHUHan-hua2,CHAOChun-feng1

(1.Department of Civil Engineering,Zhejiang University,H angzhou 310058,P.R.China; 2.Zhejiang H ighway A dm inistration,H angzhou 310058,P.R.China)

Bottom continuity tendons induce transverse additive effect while providing longitudinal com pression during the construction of PC box girder.Taking a cross-sea bridge for examp le,the mechanism of bottom continuity tendon is investigated.The transverse effect and param eters study are conducted through a refined m odel.It is illustrated that the state of bottom flange is in a dynamic changeable process during the tensioning of bottom continuity tendons,and the transverseeffect caused by the tendons ismuchmore than thatby dead loading and other prestressing tendons.The transverseeffect is more sensitive to alignment and thickness of the bottom flange,as well as concrete cover of the ducts. Finally,based on the sim plified frame analysis,the design method is proposed by introducing prestressing effect sim plified factor and ductmodified factor.

bridge engineering,box girder,bottom continuity tendon,transverse effect,parametric study

U448.35

A

1674-4764(2011)03-0025-06

2010-12-15

浙江省交通厅科技项目(2008H 38)

项贻强(1959-),男,教授,博士生导师,主要从事桥梁结构的非线性理论、健康监测与控制、桥梁加固、古桥的保护与管理,(E-mail)xiangyiq@zju.edu.cn。