滑坡空间预测中信息量模型的改进及应用

赵 衡,宋二祥

(清华大学土木工程系,北京 100084)

滑坡空间预测中信息量模型的改进及应用

赵 衡,宋二祥

(清华大学土木工程系,北京 100084)

确定未来可能发生滑坡的区域,即滑坡空间预测对城乡土地规划具有重要的指导意义。针对国内在滑坡空间预测中应用较多的信息量模型,通过理论推导表明其使用前提是各影响因素相互独立,以一简单算例说明了在滑坡空间预测中因素间相关性对预测结果的影响,并建议引入因子分析评估和减少各因素间的相关性。将基于因子分析的信息量模型应用于某一流域,统计了具有连续性特征的影响因素与滑坡概率之间的关系,结合以往的研究和分析表明滑坡概率随各因素的变化趋势具有一定的规律,并基于此建议了对影响因素进行状态离散化的方法。以5年前的滑坡作为输入数据,用近5年内的滑坡对预测结果进行了验证,表明信息量模型能较好地预测未来发生滑坡的区域。

滑坡;信息量模型;影响因素;离散化;因子分析

滑坡每年都造成大量的人员伤亡和财产损失,人类对山区土地需求的增加加剧了滑坡可能带来的危害。为了减小其危害,除了加强滑坡监测治理外,更重要的是在土地规划阶段避开滑坡重灾区。滑坡空间预测的目的即为划出较易发生滑坡的地带,指导山区的土地规划和利用,并通过耦合降雨信息起到预测预警作用[1]。由于在较大区域内难以获取力学方法所需参数,滑坡空间预测主要基于工程地质类比的思想[2],即根据一些较易获得的地质水文数据,对比历史滑坡分布,认为条件相似的地区发生滑坡的可能性相同。

GIS技术使滑坡空间预测逐渐从定性判断发展为一种基于数据统计的定量分析,方法包括信息量模型[2-4]、逻辑回归模型[5-6]、神经元网络[5-6]、概率比模型[5-6]、判别分析[7]、证据权重法[8]、模糊理论[9]等。Pradhan等[5]曾比较上述部分预测方法,认为逻辑回归模型的预测结果较好,而Yilm az[6]却认为神经元网络要好一些。整体上,逻辑回归模型在国外应用较普遍,而中国应用信息量模型较多。

基于中国应用较多的信息量模型,讨论了影响因素之间的相关性对预测结果的影响。以美国西海岸Mattole流域为例,分析了滑坡概率随影响因素的变化趋势,在此基础上建议了对连续性变量进行状态离散化的方法。采用基于因子分析的信息量模型对该流域内的滑坡分布进行了预测,并验证了预测结果。

1 信息量模型

信息量模型由赵鹏大等[10]从前苏联引入中国并应用于找矿,后逐渐应用于滑坡空间预测。信息理论认为信息量的增加代表随机事件不确定性的减少,对于滑坡来说,信息量越大,发生滑坡的可能性越大。该模型即通过计算预测区域内各处关于滑坡的信息量以达到滑坡空间预测的目的。

1.1 信息量模型的理论推导

选择n个对滑坡有影响的因素,表示为Xi(i= 1,…,n),Xi取不同的值代表第i个因素不同的状态。发生滑坡表示为Y,单个因素Xi对滑坡提供的信息量为Ii,n个因素对滑坡提供的总信息量为I,Ii和I可分别表示为[2]：

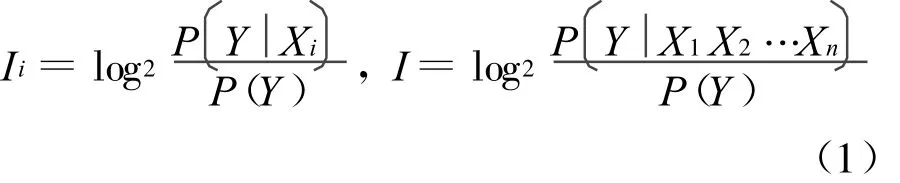
按照信息量模型的实际计算过程,认为总信息量为各因素提供的信息量之和,即：

实际上,根据式(1)并不能从数学上直接导出式(2)中信息量的计算方法,需要引入较严格的假定,包括：1)各影响因素之间的相互独立;2)滑坡发生条件下各影响因素之间的相互独立,即：

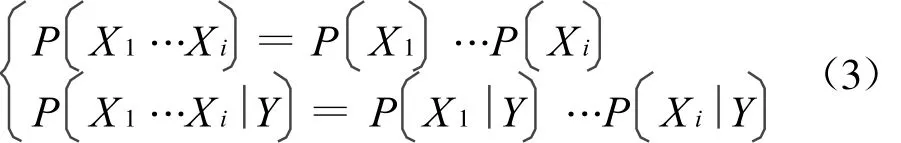
其中,i=2,…,n。在式(3)成立的条件下可以推出：

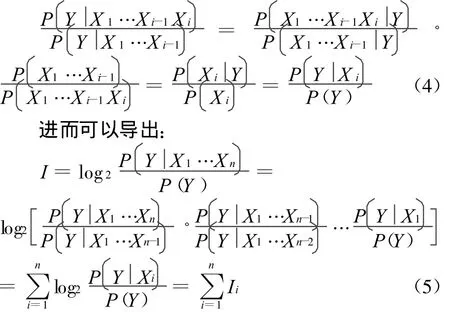
需要说明的是,式(3)是式(2)成立的充分非必要条件。

1.2 影响因素相关性对预测结果的影响

上述对信息量模型的推导过程说明,式(2)成立需要满足各因素间相互独立,当因素之间的相关性较强时得到的预测结果可能与实际不符。表1中的特殊算例可直观地说明相关性对预测结果的影响,区域内有4类单元,选择高程、坡度、岩性3个影响因素进行滑坡预测,每个因素对应2种不同状态,其中坡度和高程二者完全相关。根据信息量模型,在将预测区域划分为面积相等的网格单元条件下,因素Xi所对应的某一状态的信息量可根据历史滑坡计算得到[2],即：

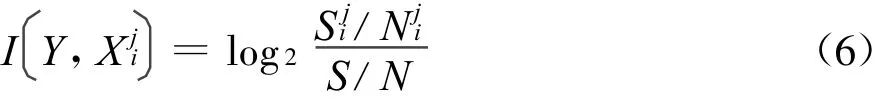
其中,N和S分别表示整个预测区域的单元总数和历史上发生滑坡的单元总数;分别表示所对应的单元数和其中历史上发生滑坡的单元数。根据式(6),可以计算出3个因素的不同状态所对应的信息量：岩性(A～0.68,B～-1.32)、坡度(＞20°～0.42,＜20°～-0.59)、高程(＞100 m～0.42,＜100m～-0.59),进而得到总信息量如表1所示。从中可以看出,总信息量的计算结果显示单元②和③发生滑坡的可能性相同,而实际上单元②发生滑坡的概率是单元③的2倍;倘若只考虑岩性和坡度2个因素,得到的信息量与滑坡所发生的概率一致。

表1 因素之间的相关性对预测结果的影响

上述算例说明,由于因素间的相关性,在计算某一因素的信息量时实际包含了多个因素的共同作用,因而在最后得到的总信息量中,重复考虑了具有相关性的因素对滑坡的作用,并相对地减弱了其它因素的影响,使得预测结果与实际有较大差异。

2 影响因素与滑坡的关系

影响因素是指对滑坡的发育具有一定作用的各种水文地质环境条件,其中如坡度等部分因素是连续性变量,采用信息量模型前需将其离散为各种状态。为此,基于历史滑坡分布分析了Matto le流域内滑坡概率随这些因素的变化趋势,在此基础上建议了状态离散化的方法。

2.1 数据搜集整理

Mattole河流域位于美国西海岸,地理坐标为西经123°54′～124°22′,北纬39°58′～40°25′,整个流域的面积约为965 km2,如图1所示。该流域年均降雨量较大,约为150～290 cm/a,且位于典型地质构造活动区,每年因降雨或地震诱发大量滑坡。

为了有效预测滑坡,所选择的影响因素应是对滑坡的发育有控制作用的因素,而实际某些重要因素如地下水的数据很难获取,而只能采用其他因素如河流、植被等来间接反映其影响。目前文献中常用的影响因素有50多种[11],有些因素对滑坡有直接作用,如坡度、坡面曲率等;而有些的作用是间接的,如道路、覆盖层,边坡朝向等。本文选取其中使用频率较高的坡度、边坡朝向、坡面曲率、累积汇流面积、岩性、断层、土壤质地、河流、道路、郁闭度、覆盖层等11个影响因素,相应的数据如下：

1)滑坡分布,如图2中分为5年前和5年内滑坡;

2)分辨率为10 m×10m的DEM数据;

3)工程地质图;

4)土壤质地分布;

5)河流分布;

6)道路分布;

7)郁闭度分布;

8)覆盖层分布。

其中,利用A rcGIS软件可根据DEM数据计算得到流域内的坡度、边坡朝向、坡面曲率以及累积汇流面积等变量的分布;根据工程地质图可以提取出流域内的岩性和断层分布。

图1 Mattole流域位置示意图

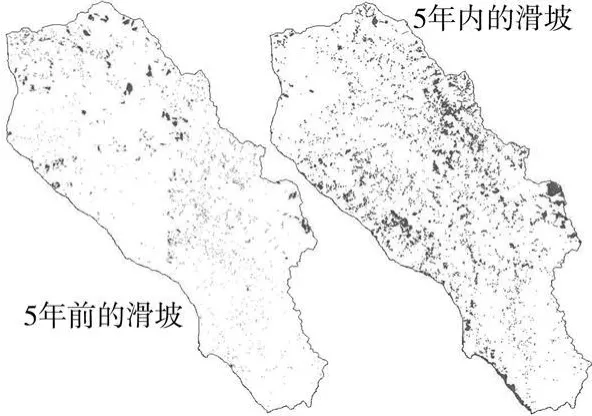
图2 滑坡分布

2.2 滑坡概率随部分因素的变化趋势

所选取的影响因素中,坡度、边坡朝向、坡面曲率、累积汇流面积、郁闭度以及距离断层、河流、道路的距离等8个因素为连续性变量,对比5年前的滑坡,分析了历史滑坡概率随各因素的变化规律。为了计算各因素不同取值所对应的滑坡概率,首先将各因素划分为不同的取值区间,并使各区间对应的区域有近似相同面积,为保证统计上的意义,该面积不宜太小。然后计算各区间所对应区域内滑坡区域的面积所占比例,以此作为该取值区间中值所对应的滑坡概率。

1)坡度 坡度决定了滑动体的下滑力大小,理论上坡度越大,发生滑坡的可能性越大。实际上,坡度很大的区域往往是出露岩层,因而当坡度为中间大小时发生滑坡的可能性最大,如图3所示,图中虚线为整个预测区域内发生滑坡的平均概率。从中可以看出,所研究流域内坡度为18°左右时滑坡概率最大,大于或小于这个坡度时,滑坡概率均逐渐变小。

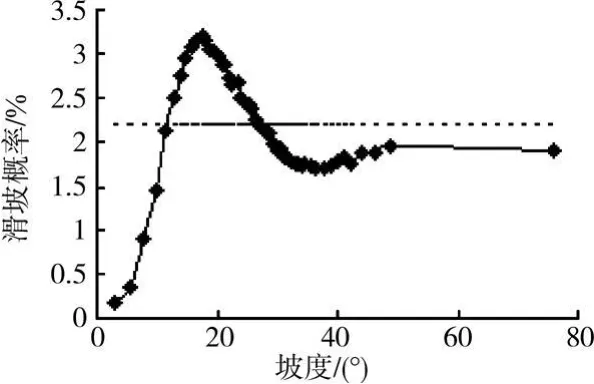
图3 坡度与滑坡概率的关系

2)边坡朝向 研究表明边坡朝向对滑坡的发育有影响[5-7],反映在阳光照射影响到土壤湿度和地表植被,进而影响土体强度;另外在降雨时边坡朝向还影响到地表实际降雨量[12],而土体强度和地表降雨量都对滑坡有直接影响。图4为不同边坡朝向对应的滑坡概率,朝向从正北方向开始,顺时针计算。从中可以看出,所研究流域内边坡朝向位于130°～220°时,滑坡概率相差不多且明显高于其它朝向,而边坡朝向小于130°或大于220°时,滑坡概率整体上逐渐减小。

3)坡面曲率 坡面曲率反映了地形的凹凸,其中凸为正,凹为负。以往研究认为凹形地面汇水能力强,发生滑坡的可能性最大,而忽视了地形本身对边坡稳定性的影响[13]。由于水平凹形边坡的稳定性要高于长直坡,因而并非坡面越凹发生滑坡的可能性越大,如图5所示。从中可以看出,所研究流域内曲率为-0.7 m-1即坡面稍凹时的滑坡概率最大,大于或小于该曲率时滑坡概率整体上均逐渐减小。

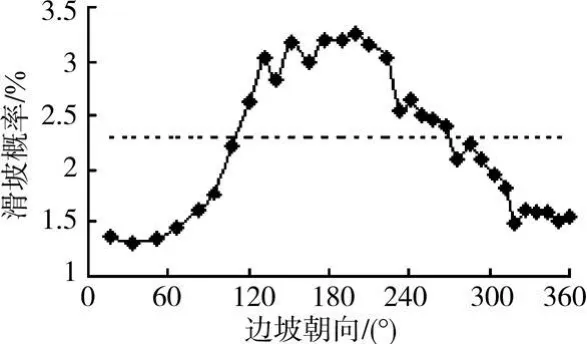
图4 边坡朝向与滑坡概率的关系

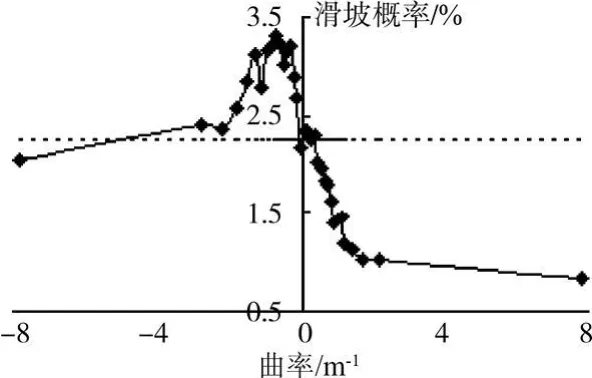
图5 坡面曲率与滑坡的关系

4)累积汇流面积 图6为累积汇流面积与历史滑坡概率之间的关系,汇流面积用栅格个数表示。累积汇流面积越大代表能汇集的雨水越多,发生滑坡可能性越大[7],但累积汇流面积很大的区域往往是河流,不具备发生滑坡的条件。因而如图6所示,所研究流域内累积汇流面积小于10时,滑坡概率随着累积汇流面积的增加而增加;而当累积汇流面积大于10以后,滑坡概率大致随着累积汇流面积的增加而减少。

5)郁闭度 郁闭度是指乔木树冠遮蔽地面的程度,它反映了树木的覆盖密度。树木根系能起到加强土体强度的作用,树叶还可以缓解雨水对地面的冲刷,因而郁闭度越大,发生滑坡的可能性越小,如图7所示。

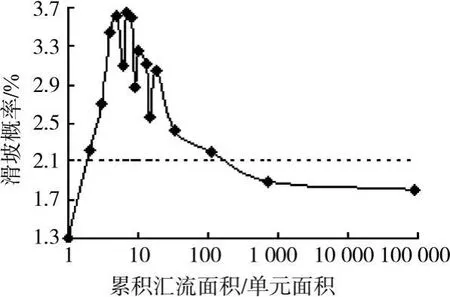
图6 累积汇流面积与滑坡的关系

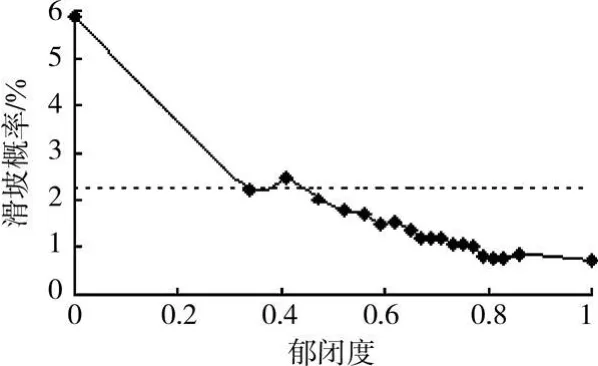
图7 郁闭度与滑坡的关系

6)断层 图8为断层不同缓冲宽度内的滑坡概率。一般认为断层附近裂隙多、岩体破碎,是滑坡较发育的地区。但从图中来看,滑坡概率并非在断层附近较大,且其变化趋势没有明显规律,已有研究也发现了同样现象[14],这可能与所获得的数据中断层和滑坡数据不完整有关。尽管断层是较重要的影响因素,但考虑到当前数据无法反映其实质影响以及可能对预测结果带来干扰,计算时将舍去断层这一因素。

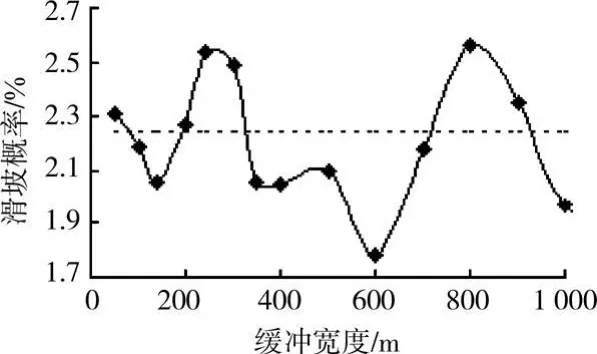
图8 断层与滑坡的关系

7)河流 河流对滑坡的影响主要有2个方面,一是河流的掏蚀容易产生临空面;二是河流一定程度上反映了下雨时的水流方向,影响到雨水的下浸深度。一般认为河流附近区域发生滑坡的可能性较大。图9为河流不同缓冲宽度内的滑坡概率,从中可以看出,在150 m缓冲宽度内滑坡概率高于平均概率,而在150～400 m缓冲宽度内要低于平均概率,这一定程度上验证了河流对滑坡的影响。当缓冲宽度大于400m时,滑坡概率明显变大,显然这不是河流的作用,或者认为河流的影响范围有限。

8)道路 因为修建道路会形成临空面,还可能引起岩体松动,一般认为道路附近区域容易发生滑坡。但考虑到道路选址时会尽量避开滑坡重灾区,如果护坡做得较好也可有效防止滑坡,因而道路附近区域发生滑坡的概率反而可能较小,如图10所示,整体上离道路越近的区域发生滑坡的概率越小。

图9 河流与滑坡的关系

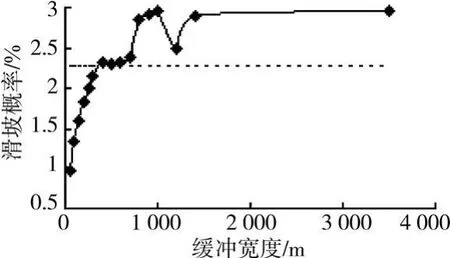
图10 道路与滑坡的关系

3 影响因素的离散化及相关性分析

3.1 影响因素的不同状态

采用信息量模型时,各影响因素都有不同的状态,状态相同意味着对滑坡的作用相同。离散性影响因素如岩性等根据其名称分别对应不同状态,而对于为连续性变量的影响因素则需要进行状态离散化。根据上文中滑坡概率随影响因素的变化趋势,可采用如下步骤进行离散化,以图3中坡度与滑坡的关系曲线为例首先划出滑坡概率大致相同的区间,如坡度＞40°时滑坡概率大致相同;然后以整个区域发生滑坡的平均概率对应的坡度为断点,即11°、29°;再划分出滑坡概率很高或很低的区间,如坡度为18°时滑坡概率最高,可在其附近划分出区间11°～15°;如上述得到的区间内滑坡概率变化幅度较大,可进一步离散,如坡度＜11°时,滑坡概率为0.16%～2.24%,进一步离散为0°～8°、8°～11°两个区间。由此得到坡度、边坡朝向、坡面曲率、累积汇流面积、岩性、土壤质地、河流、道路、郁闭度、覆盖层等10个影响因素及其相应的状态如表2所示。其中在所研究流域内滑坡概率随岩性、土壤质地、覆盖层等影响因素的变化如图11-13所示。

3.2 各因素的相关性分析

根据上文分析,因素间的相关性可能导致不符合实际的预测结果。为此,采用因子分析对表2中影响因素间的相关性进行了评估。因子分析是一种多元统计方法,它通过少数互不相关的“抽象”变量来表示实际变量,它除了可以降维、简化数据外,还可用于研究众多变量之间的内部依赖关系[15]。

表2 所选定的影响因素及其状态

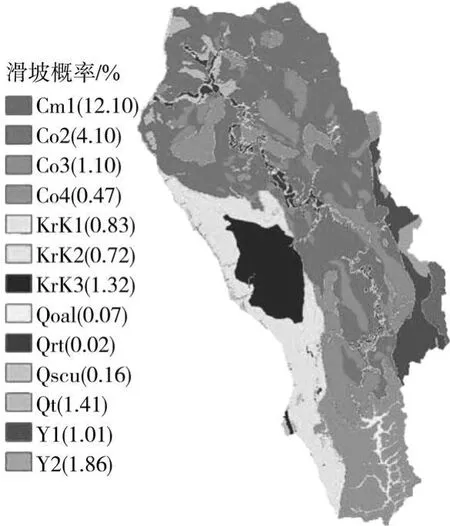
图11 滑坡概率随岩性的分布

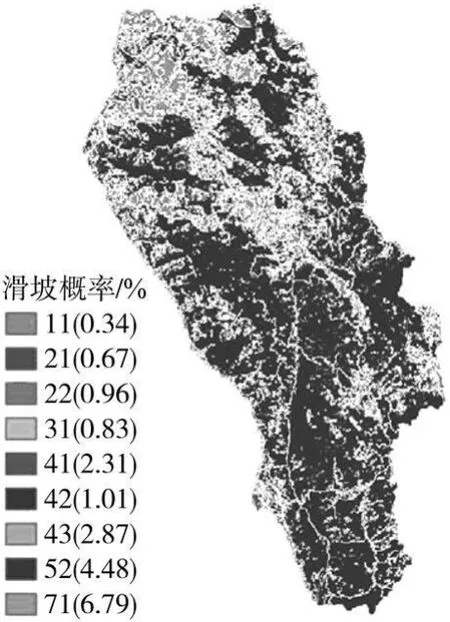
图13 与滑坡概率随地面覆盖层的分布

因子分析前需要采用不同数值代表各因素的不同状态,考虑到只有在联合正态分布条件下互不相关才与相互独立等价,在对各状态进行赋值时尽量使各影响因素满足正态分布。采用SPSS统计分析软件,使新生成的因子反映至少95%的差异性,得到因子分析的结果如表3所示。从中可以看出,每个影响因素均在不同且唯一的新因子上具有接近于1的权重,而在其它因子上的权重绝大多数小于0.1。由此说明,表2中各影响因素之间的相关性不明显,可以直接用其进行滑坡空间预测。需要说明的是,若几个影响因素间的相关性很明显,即在同一个新因子上具有较大权重,则可用新因子代替原来的影响因素,以避免相关性对预测结果的影响。

4 预测结果及验证

在上述分析的基础上,以5年前的滑坡作为输入数据,对Mattole流域的滑坡空间分布进行了预测,并与近5年内的滑坡进行了对比验证。

4.1 计算过程及结果

利用A rcGIS分析计算功能,信息量模型的计算过程较为简单：首先,根据式(6)和历史滑坡分布计算得到各影响因素不同状态所对应的信息量值,得到单因素信息量图层;然后根据式(2)将单因素信息量图层叠加,得到整个区域的信息量分布。

将Matto le流域分为1.19×107个94 m×94 m的栅格单元,根据其中5年前的滑坡分布,共有滑坡单元2.67×105个,按照上述步骤得到整个区域的信息量分布,如图14。由于信息量反映了发生滑坡可能性的相对大小,信息量值越大发生滑坡的可能性越大,因而图14也可称之为易滑度分布。

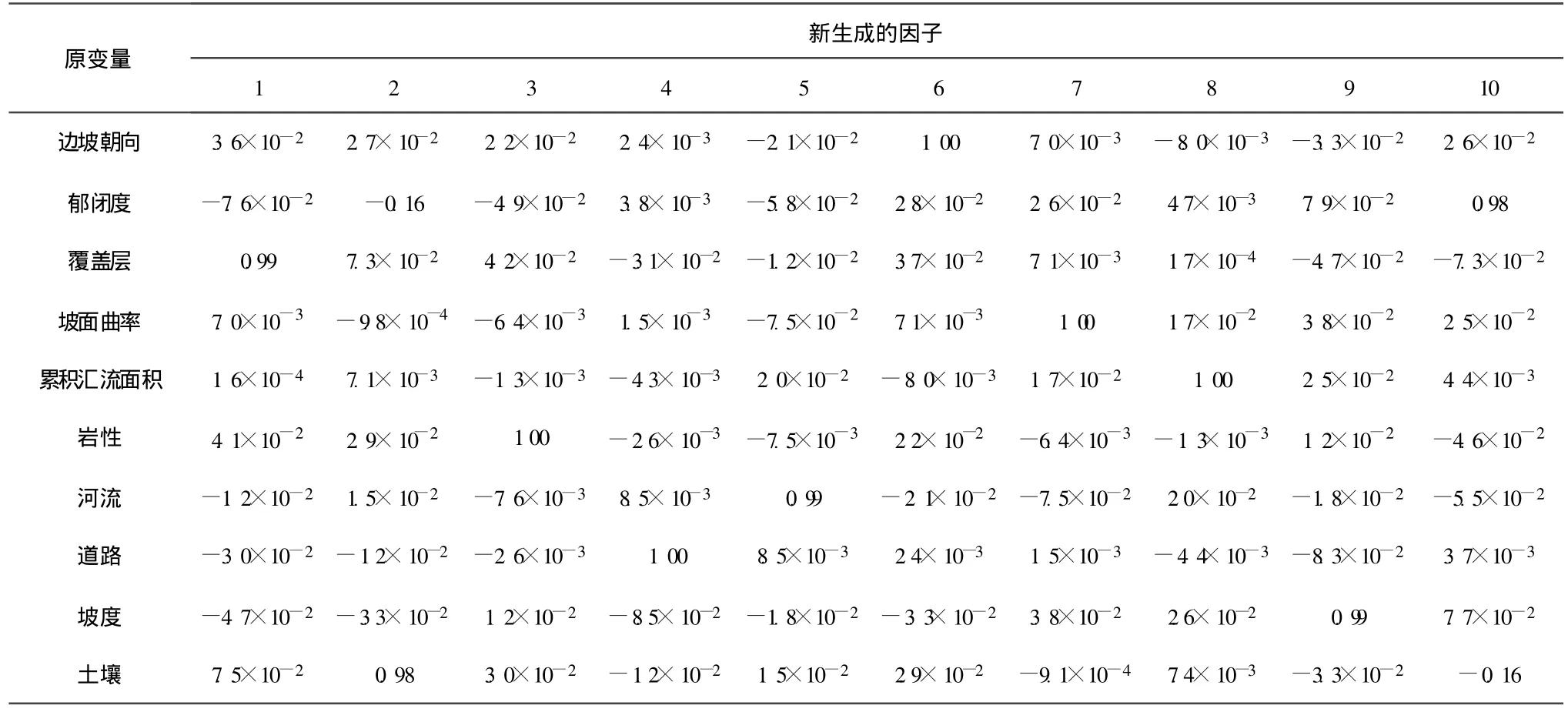
表3 影响因素的因子分析结果

4.2 结果的验证和评价

滑坡空间预测结果的好坏需要对比实际滑坡的分布,目前文献中大多将预测结果与预测时所输入的滑坡分布对比,不能反映其对未来滑坡的预测能力。该文将5年前的滑坡作为输入数据,采用近5年内的滑坡分布来对预测结果进行评价。

对比图14中的易滑度和图2中的滑坡分布,可以看出易滑度较高的区域滑坡分布密度就大,即预测结果与实际较为吻合。进一步采用“面积比”评价指标[16]对结果进行定量化评价,该指标定义为：

式中,p为整个预测区域平均滑坡概率;S为预测率函数与X轴所围面积。预测率函数是指将所有栅格按易滑度从大到小排序后,按顺序取出不同比例栅格中的滑坡栅格占所有滑坡栅格的比例。由图13所示的易滑度分布,对比5年前和5年内的滑坡,得到相应的预测率函数曲线和预测精度如图15所示。从中可以看出,图13的预测结果与5年前滑坡对比的准确度为0.79,对“未来”5年内滑坡预测的准确度为0.71。由此说明,信息量模型能较好地用于预测未来滑坡的空间分布。

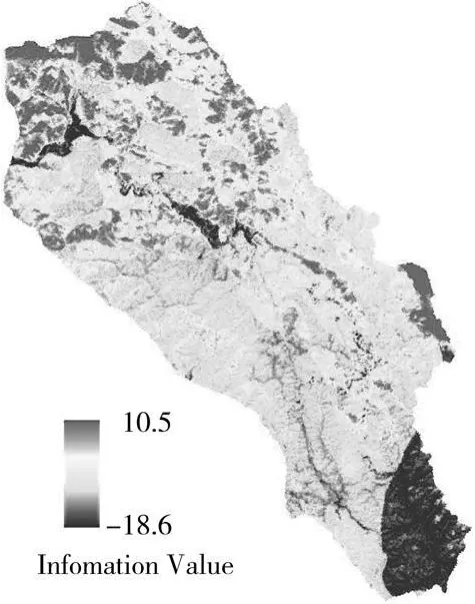
图14 预测区域内的信息量分布

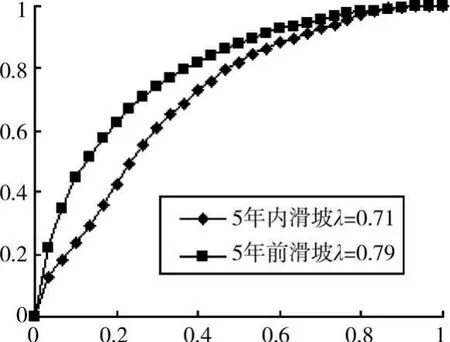
图15 预测率函数曲线

5 结 语

1)滑坡空间预测选取一些较易获取其分布数据且对滑坡有直接或间接影响的因素,通过统计分析方法比较因素间相似性,能较好地划分出区域内容易发生滑坡的地带。

2)理论推导和算例表明,采用信息量模型时,影响因素间的相关性可能导致预测结果与实际不符,可引入因子分析评估和减小因素间的相关性。

3)统计了所研究流域内滑坡概率随部分影响因素的变化趋势,尽管是某个特定流域的统计结果,但从文中分析和已有研究可以看出,上述变化趋势在不同区域内具有一定的普遍性。

4)基于滑坡概率随影响因素的变化趋势,建议了对影响因素中连续性变量进行状态离散化的方法。

5)采用5年前滑坡作为输入数据进行了预测,并用近5年内的滑坡对预测结果进行了定量化的评价,表明信息量模型能较好地用于滑坡空间预测。

致谢：该文所用Mattole流域数据来源于加州保护部,在此表示衷心感谢!

[1]张桂荣,殷坤龙,刘礼领,等.基于WEB的浙江省降雨型滑坡预警预报系统[J].地球科学—中国地质大学学报,2005,30(2)：250-254.

ZHANG GUI-RONG,YIN KUN-LONG,LIU LI-LING, et al.Warning system for rain-induced landslides based on Internet in Zhejiang province,China[J].Earth Science—Journal of China University of Geosciences,2005,30(2)：250-254.

[2]殷坤龙.滑坡灾害预测预报[M].武汉：中国地质大学出版社,2004.

[3]JADE S,SARKAR S.Statistical models for slope instability classification[J].Engineering Geology, 1993,36：91-98.

[4]孟令超,卢晓仓,史晨晓,等.基于信息量模型的达曲库区滑坡危险性分析[J].灾害学,2009,24(4)：31-34.

MENG LING-CHAO,LU XIAO-CANG,SH ICH ENXIAO,et al.Analysis on landslide hazard risk in Daqu reservoir area based on information value model[J]. Journal of Catastrophology,2009,24(4)：31-34.

[5]PRADH AN B,LEE S.Delineation of landslide hazard areas on Penang Island,Malaysia,by using frequency ratio,logistic regression,and artificial neural netw ork model[J].Environ.Earth Sci.,2009,DOI：10.1007/ s12665-009-0245-8.

[6]YILMAZ I.Landslide susceptibilitymapping using frequency ratio,logistic regression,artificialneural networks and their comparison：A case study from Kat landslides(Tokat—Turkey)[J].Computer&Geosciences,2009,35：1125-1138.

[7]BAEZA C,COROMINAS J.Assessment of shallow landslide susceptibility by means of multivariate statistical techniques[J].Earth Surface Process and Land form s,2001,26：1251-1263.

[8]OH H J,LEES.Landslide susceptibilitymappingon Panaon Island,Philippines using a geographic information system [J].Environmental Earth Sciences,2010,DOI：10.1007/ s12665-010-0579-2

[9]KANUNGO D P,ARORA MK,SARKARS,eta l.A fuzzy set based approach for integration of thematic maps for landslide suscep tibility zonation[J]. Assessment and Management of Risk for Engineered Systems and Geohazards,2009,3(1)：30-43.

[10]赵鹏大,胡旺亮,李紫金.矿床统计预测[M].北京：地质出版社,1983.

[11]LIN Y H.Application of neural netw orks to landslide susceptibility analysis[D].Taiw an：National Central University,2003.

[12]DA IFC,LEE C F.Landslide characteristics and slope instability modeling using GIS,Lantau Island,H ong Kong[J].Geomorpho logy,2002,42：213-228.

[13]OH LMACHER G C.Plan curvature and landslide p robability in regions dom inated by earth flow s and earth slides[J].Engineering Geo logy, 2007,91：117-134.

[14]李媛.区域降雨型滑坡预报预警方法研究[D].北京：中国地质大学,2005.

[15]朱建平.应用多元统计分析[M].北京：科学出版社,2006.

[16]赵衡,宋二祥.滑坡灾害空间预测结果的评价方法[J].自然灾害学报,2010,19(5)：36-41.

ZHAO HENG,SONG ER-XIANG.Assessmentmethod for results of the spatial prediction of regional landslides[J]. Journal of Natural Disasters,2010,19(5)：36-41.

(编辑 王秀玲)

Improved Information ValueModel and Its App lication in the Spatial Prediction of Landslides

ZHAOHeng,SONGEr-xiang
(Departmentof Civil Engineering,Tsinghua University,Beijing 100084,P.R.China)

In formation Value Model is used frequen tly in domestic landslide hazard zonation prediction, which plays a very important ro le for land-use p lanning especially in mountain area.Through theoretical analysis,the prerequisite of Information Value Model which should be used w ith influence-factors independent from each other is studied.Factor Analysis isadopted to evaluate and elim inate the influence of correlation between in fluence-factors in spatial p rediction of landslides which are show ed through case study.Relationships betw een landslides and in fluence-factors are studied based on a certain watershed in which the Information Value Modeland Factor Analysis are app lied.The probability of landslides changes regularly with the influence-factors,and based on which amethod for the discretization of influence-factors is advised.The distribution of landslide suscep tibility of above watershed is calcu lated and validated based on the area-ratio index w ith landslides occurring in nearly 5 years,which p roves the credibility of Information Value Model.

landslides;inform ation valuemodel;influence-factors;discretization;factor analysis

P642.22

A

1674-4764(2011)03-0038-07

2010-10-25

国家科技支撑计划(2008BAJ06B01-5)

赵 衡(1983-),男,博士生,主要从事滑坡预测研究,(E-mail)zhao-h@mails.tsinghua.edu.cn。