自行火炮固有频率特性实验研究

王宝元，刘朋科，衡刚，邵小军，喻华萨，吴会民

(西北机电工程研究所，陕西 咸阳712099)

自行火炮悬挂系统特性不仅对乘员的工作能力、火炮射击精度、火炮构件强度有重要影响，同时，也对自行火炮的机动性有重要影响［1］。因此，研究自行火炮结构动态特性、尤其是自行火炮悬挂系统动态特性更为重要。由于自行火炮悬挂系统的存在，自行火炮全系统振型中包括全炮的前后俯仰振型、上下平动振型和左右横滚振型，这些振型都有对应的固有频率，它们对自行火炮结构动态特性产生着不同的影响。由于悬挂系统结构和特性的较大差异，构造出了轮式自行火炮和履带式自行火炮。自行火炮的低阶模态主要表现为全系统在悬挂弹性、轮胎或履带橡胶挂脚弹性支撑下的刚体运动，这些刚体运动有全系统的前后俯仰、上下平动和左右横滚。这些刚体模态的固有频率与结构弹性支撑及悬挂质量有关。本文分别选择2 门口径不同的轮式自行火炮(分别称其为轮式自行火炮A 和轮式自行火炮B)和2 门口径不同的履带式自行火炮(分别称其为履带式自行火炮A 和履带式自行火炮B)为研究对象，采用试验模态分析方法进行全炮结构动态特性规律研究，研究轮式与履带式自行火炮低阶模态振型，获取对应的固有频率。研究轮式自行火炮与履带式自行火炮低阶振型及其固有频率的差异，研究其产生差异的原因，研究轮式自行火炮与履带式自行火炮进行试验模态分析时应采取的正确试验方法。

1 传统试验模态分析法

通过测量工程结构在非工作状态下的激振力和响应，进而采用频响函数或脉冲响应函数来识别模态参数的方法称其为传统试验模态分析法，或称测力试验模态分析法为传统试验模态分析法［2］。

传统试验模态分析法是一种最常用的试验方法。传统试验模态分析系统是由激励系统、响应和激励力测量系统及分析计算系统组成，通过传统试验模态分析可以得到火炮各部件及全炮的动力学固有特性。借助于力锤或激振器，在试验结构上施加一定频带宽度的激励力{f(t)}，它的振动响应{x(t)}也是一个包含了系统模态信息的信号。对激励力和响应经过快速傅里叶变换(FFT)后得到相应的傅里叶谱F(ω)和X(ω)，则频响函数矩阵为

这样，通过对施加到结构上的激励信号和结构上各测点的响应信号的分析处理，就可以得到表征结构系统特性的传递函数矩阵，再经过计算识别就可以得到结构的固有特性，即模态参数。

2 工作模态分析法

仅利用工作状态或环境激励下的响应信号识别结构模态参数的试验方法称其为工作模态分析方法，或称不测力试验模态分析法为工作模态分析方法［3-7］。

工作模态分析亦称为环境激励下的模态分析，采用工作模态分析方法得到的工作振型(ODS)表现的是在工作状态下的某个特定频率或时刻，结构上的两点或多点之间的相对振动，或一个点相对于其他所有点的振动状态。工作模态分析的基本思想是两个响应点之间的互相关函数和脉冲响应函数有相似的表达式，求得2 个响应点之间的互相关函数后，可以运用时域中的模态参数识别方法进行模态参数识别。在未知激励的情况下，工作振型频率响应函数(ODS FRF)是分析工作状态下结构振型的理想方法，ODS FRF 是计算工作状态下响应数据间的频率响应函数，把某一点的响应信号作为参考点信号，其他点响应信号为流动响应信号。ODS FRF 计算的是流动响应信号与参考响应信号之间的互谱，用流动响应信号自谱幅值的平方根来代替互谱的幅值可以获得正确的幅值，通过计算互谱确保了不同的测量组响应数据之间有正确的相位信息。因此，ODS FRF 是由流动响应信号自谱的幅值和流动响应信号与参考响应信号互谱的相位构成，其数学表达式为:

式中:Gxy(ω)=Fx(ω)F*y(ω)为流动响应信号与参考点响应信号的互谱;Gxx(ω)=Fx(ω)F*x(ω)为流动响应信号的自谱。

如果激励谱在模态存在的频率范围内相对平缓，即近似白噪声激励，那么便可以利用常规的频响函数拟合方法对ODS FRF 曲线进行拟合而得到模态参数。

频响函数矩阵模型包含频响函数曲线、激励傅氏谱和位移响应傅氏谱。模型中的每个元素都可以表示为:

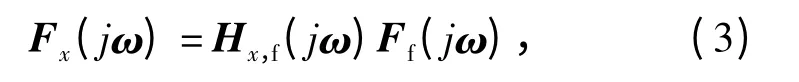
式中:Fx(jω)为响应信号的傅氏谱;Ff(jω)为激励信号的傅氏谱;Hx，f(jω)为激励与响应信号的传递函数。

如果假设激励在模态频率范围内满足白噪声激励条件，则傅氏谱的幅值可以用一常数来代替，即

系统的响应与频响函数成正比关系，即

由上述分析可知，系统的模态频率、模态阻尼和模态振型信息都包含在工作振型频响函数与工作振型之中。ODS FRF 表达式与频响函数形式相类似。因此，可以将已经很成熟的频响函数拟合方法稍加改动，就能够用于拟合各响应点信号同参考点信号之间的ODS FRF，从而求出模态参数。

3 轮式和履带式自行火炮试验模态分析

分别选择2 门口径不同的轮式自行火炮及其对应的履带式自行火炮为研究对象，采用试验模态分析方法进行全炮结构动态特性规律研究，研究轮式与履带式自行火炮低阶振型，也就是全炮系统的前后俯仰振型、上下平动振型和左右横滚振型规律，获取对应的固有频率，分析轮式自行火炮与履带式自行火炮低阶振型及其固有频率的差异。

采用传统试验模态分析法和工作模态分析法进行全炮试验模态分析。试验时，自行火炮停放在平坦的水泥地面上，在火炮结构上布置振动响应测点，采用加速度传感器拾振。采用传统试验模态分析法，选择火炮底盘顶甲板四角结构刚度较大的一个位置作为激励点，用力锤单点固定位置激励，通过记录激励力信号，拾取全部测点加速度响应信号，完成传统试验模态分析。启动自行火炮发动机来激励试验对象，不用记录激励力信号，只记录全部测点加速度响应信号，完成工作模态分析试验及模态参数识别。传统试验模态分析法和工作模态分析法相同之处在于，都通过加速度传感器和动态信号分析仪拾取、记录测点加速度响应信号，以此形成传递函数，然后进行模态参数识别。2 种方法不同之处在于，传统试验模态分析法必须用力传感器(如力锤)去激励试验对象，并记录激励力的大小和规律;而工作模态分析法却不必记录激励力信号，仅依靠测点的加速度信号及分析软件，就可识别出结构的模态参数。

为了验证工作模态分析法在自行火炮上的应用效果，以轮式自行火炮A 为试验对象，分别采用传统试验模态分析法和工作模态分析法进行对比试验。通过试验模态分析，得到了全系统在50 Hz 频率范围内的模态频率和模态振型。图1是轮式自行火炮A 全炮测点布置。图2～图4分别给出了轮式自行火炮A 高低振动模态振型图，表1给出了经过试验识别出的模态频率。结果表明，工作模态分析法试验结果与传统试验模态分析法试验结果一致，在全炮系统前3 阶振型中，第1 阶振型为全炮系统俯仰振动模态，第2 阶振型为全炮系统上下平动模态，第3 阶振型为全炮系统横滚振动模态。工作模态分析法得到的前3 阶固有频率分别为2.90，3.89，5.20 Hz.

图1 轮式自行火炮A 全炮系统测点布置Fig.1 Layout of test points for wheeled self-propelled gun A

图2 轮式自行火炮A 第1 阶振型(全炮前后俯仰)Fig.2 First-order mode of self-propelled gun A

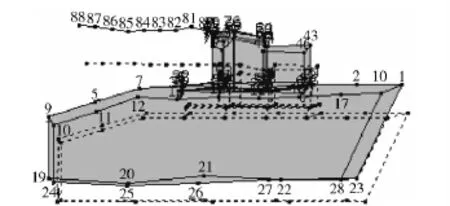
图3 轮式自行火炮A 第2 阶振型(全炮上下平动)Fig.3 Second-order mode of self-propelled gun A

图4 轮式自行火炮A 第3 阶振型(全炮左右横滚)Fig.4 Third-order mode of wheeled self-propelled gun A

同样，采用工作模态分析方法，对履带式自行火炮A 和履带式自行火炮B 全炮进行了试验，采用传统试验模态分析法进行了轮式自行火炮B 试验，固有频率识别结果如表2所示。由于篇幅的限制，图5～图7仅给出了履带式自行火炮A、轮式自行火炮B 和履带式自行火炮B 第1 阶振型图。试验时发现，传统试验模态分析法对履带式自行火炮全系统低阶模态参数识别效果不佳，因此，履带式自行火炮均采用工作模态分析方法进行模态参数识别。

表1 工作模态分析法与传统试验模态分析法结果Tab.1 Analysis results of operational modal and traditional modal methods

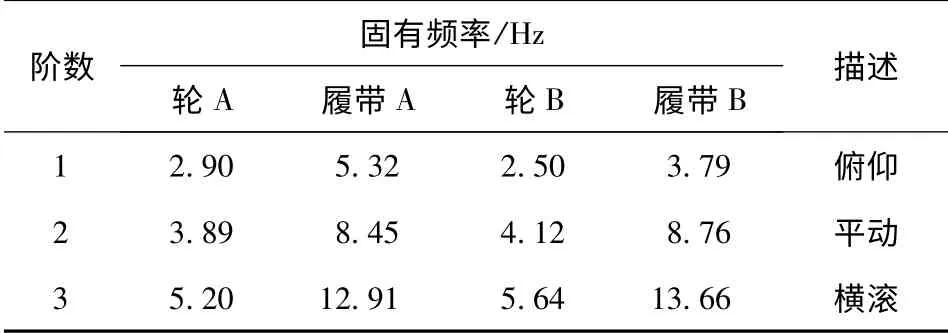
表2 轮式自行火炮与履带式自行火炮低阶固有频率对比Tab.2 Comparison between natural frequencies of wheeled and tracked self-propelled guns

图5 履带式自行火炮A 第1 阶振型(频率5.32 Hz，全炮前后俯仰)Fig.5 First-order mode of tracked self-propelled gun A (frequency 5.32 Hz)

从上述试验结果可以看出，履带式自行火炮固有频率均大于轮式自行火炮。为了解释这种规律，特此进行了履带式自行火炮和轮式自行火炮悬挂等效刚度实验测试。结果表明，履带式自行火炮底盘悬挂等效刚度系数实验测试值比轮式自行火炮大1.5～3 倍左右。

4 试验结果分析与结论

分析上述试验数据，试验模态分析结果表现出的规律为:

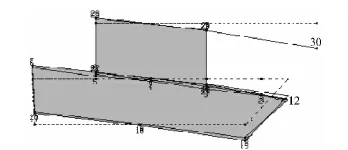
图6 轮式自行火炮B 第1 阶振型(频率2.50 Hz，全炮前后俯仰)Fig.6 First-order mode of wheeled self-propelled gun B (frequency 2.50 Hz)

图7 履带式自行火炮B 第1 阶振型(频率3.79 Hz，全炮前后俯仰)Fig.7 First-order mode of tracked self-propelled gun B (frequency 3.79 Hz)

1)在选择的4 门自行火炮中，固有频率从低到高，自行火炮全系统固有振型:俯仰、平动和横滚出现的顺序依次是，俯仰→平动→横滚，即俯仰振型对应的固有频率最低，其次是平动振型对应的固有频率，横滚振型对应的固有频率较高，轮式和履带式自行火炮都符合上述规律。

2)就本文所选火炮，履带式自行火炮全系统俯仰、平动和横滚固有振型对应的固有频率分别大于轮式自行火炮相应的固有频率。轮式和履带式火炮相同振型时，其固有频率相差1.5～3 倍左右。即履带式自行火炮全系统俯仰、平动和横滚固有频率分别大于轮式自行火炮相应振型对应的固有频率1.5～3 倍左右。

振动理论指出，对于单自由度振动系统，系统固有频率f 与系统刚度k、系统质量m 有下列关系:

即系统质量相同，当系统刚度系数大时，则系统固有频率也高。由于履带式自行火炮底盘悬挂等效刚度系数实验测试值比轮式自行火炮大，因此，履带式自行火炮全炮俯仰、平动和横滚固有频率分别大于轮式自行火炮相应振型对应的固有频率。

3)对于轮式自行火炮，不管采用传统试验模态分析法还是采用工作模态分析法，都可以得到满意的全系统俯仰、平动和横滚固有振型及其固有频率。但对于履带式自行火炮，由于履带及悬挂系统的特殊性，要得到满意的全系统俯仰、平动和横滚固有振型及其固有频率，最好采用工作模态分析法。用传统试验模态分析法进行履带式自行火炮全炮试验模态分析，要么有些测点不能记录到振动响应，要么有些振型不能被激起，该方法不能得到满意的全系统俯仰、平动和横滚固有振型及其固有频率，用传统试验模态分析法进行履带式自行火炮低频段试验模态分析有局限性。

References)

［1］ 丁法乾.履带式装甲车辆悬挂系统动力学［M］.北京:国防工业出版社，2004:1-10.DING Fa-qian.Dynamics of tracked armored vehicle suspension system［M］.Beijing:National Defense Industry Press，2004:1-10.(in Chinese)

［2］ 傅志方，华宏星.模态分析理论与应用［M］.上海:上海交通大学出版社，2000:57-80.FU Zhi-fang，HUA Hong-xing.Modal analysis theory and application［M］.Shanghai:Shanghai Jiaotong University Press，2000:57-80.(in Chinese)

［3］ 王宝元，刘朋科，衡刚，等.自行火炮工作模态分析试验技术［J］.兵工学报，2009，30(7):853-856.WANG Bao-yuan，LIU Peng-ke，HENG Gang，et al.The operational modal analysis experimental technique used for self-propelled gun［J］.Acta Armamentarii，2009，30 (7):853-856.(in Chinese)

［4］ 朱国良，王开和，卢学军，等.工作模态分析方法的应用研究［J］.天津科技大学学报，2007，22，(1):75-78.ZHU Guo-liang，WANG Kai-he，LU Xue-jun，et al.Study on operational modal analysis method of pipe system［J］.Journal of Tianjin University of Science ＆ Technology，2007，22(1):75-78.(in Chinese)

［5］ 陈林，张立民，段合朋.基于环境激励的车辆系统工作模态试验分析［J］.噪声与振动控制，2008，(6):81-84.CHEN Lin，ZHANG Li-min，DUAN He-peng.Modal testing and analysis of the vehicle system based on ambient excitation［J］.Noise and Vibration Control，2008，(6):81-84.(in Chinese)

［6］ 金新灿，孙守光，邢鸿麟，等.环境随机激励下高速客车的工作模态分析［J］.铁道学报，2003，25(3):24-28.JIN Xin-can，SUN Shou-guang，XING Hong-lin，et al.Operational modal analysis of a high speed passenger car［J］.Journal of the China Railway Society，2003，25(3):24-28.(in Chinese)

［7］ Yong-Hwa Park，Youn-sik Park.Structure optinization to enhance its natural frequencies based on rneasured frequency response functions［J］.Journal of Sound and Vibration，2000，229(5):1235-1255.