高阶变系数线性微分方程可解的充分条件

史胜楠

(陕西科技大学理学院， 陕西 西安 710021)

0 引 言

线性微分方程在很多科技领域有着广泛而重要的应用，如生态学、空间技术以及弹道计算等.目前对一阶线性微分方程的通解公式、常系数线性微分方程的求解方法和线性微分方程解的结构已有确定的结论[1-3]，但在实际应用中我们经常会遇到高阶变系数线性微分方程，一般情况下这类方程无法利用初等积分法求解，而一些特殊类型的高阶变系数线性微分方程可以通过变量代换等方法求得通解，例如欧拉方程.为了满足理论研究和实际应用的需要，人们不断地利用各种方法来研究高阶变系数线性微分方程的可解性，并且给出了很多可解类型[4-10].本文利用带导数的变量代换，讨论了三阶、四阶和五阶变系数线性微分方程常系数化的充分条件，总结其变化规律最终得到了n阶变系数线性微分方程的一个新的可积类型，同时给出实例加以验证.

1 预备知识

令z=y′-uy，则有

y′=z+uy

y″=z′+u′y+uy′=z′+uz+(u′+u2)y

y‴=z″+uz′+(2u′+u2)z+(u″+3uu′+u3)y

y(4)=z‴+uz″+(3u′+u2)z′+(3u″+5uu′+u3)z+[u‴+3(u′)2+4uu″+6u2u′+u4]y

可见，y(n+1)可用z(n)、z(n-1)、…、z′、z、y线性表示,表示规律如下：

(1)y(n+1)中z(n)的系数为1. (n=0,1,2,…)

(2)y(n+1)中z(k)的系数=[y(n)中z(k-1)的系数]+[y(n)中z(k)系数的导数].(k=1,2,…,n-1;n=0,1,2,…)

(3)y(n+1)中z的系数=[y(n)中y的系数]+[y(n)中z系数的导数].(n=1,2,…)

(4)y(n+1)中y的系数=[y(n)中y系数的导数]+u×[y(n)中y的系数].(n=0,1,2,…)

根据以上递推规律，可由y(n)的表达式推出y(n+1)的表达式.

例如:已知y(4)的表达式,利用以上规律可得

y(5)=z(4)+uz‴+(4u′+u2)z″+(6u″+7uu′+u3)z′+[4u‴+8(u′)2+9uu″+9u2u′+u4]z

+[u(4)+10u′u″+5uu‴+15u(u′)2+10u2u″+10u3u′+u5]y

经检验y(5)的表达式是正确的.

2 主要内容

对于一般形式的三阶变系数线性微分方程

P3(x)y‴+P2(x)y″+P1(x)y′+P0(x)y=f(x)

(1)

作变换

z=y′-uy

(2)

方程(1)被转化为

Q3z″+Q2z′+Q1z+Δ1y=f(x)

(3)

其中Q3=P3

Q2=P3u+P2=uQ3+P2

当以上3式同时成立时，方程(3)可化简为

z″+c2z′+c1z=f(x)/P3(P3≠0)

(4)

如上推导可得以下结论.

定理1：一般形式的三阶变系数线性微分方程

P3(x)y‴+P2(x)y″+P1(x)y′+P0(x)y=f(x)

(1)

的系数满足关系式

z″+c2z′+c1z=f(x)/P3(P3≠0)

(4)

注:定理1中方程(4)为二阶常系数线性微分方程，求出通解后，将其带入变换z=y′-uy中,此变换是关于y的一阶线形微分方程，可求通解.

利用以上方法还可以得到四阶、五阶变系数线性微分方程可解的充分条件.

定理2：一般形式的四阶变系数线性微分方程

P4(x)y(4)+P3(x)y‴+P2(x)y″+P1(x)y′+P0(x)y=f(x)

(5)

的系数满足以下关系式

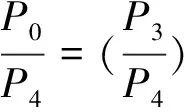
z‴+c3z″+c2z′+c1z=f(x)/P4(P4≠0)

(6)

定理3：一般形式的五阶变系数线性微分方程

P5(x)y(5)+P4(x)y(4)+P3(x)y‴+P2(x)y″+P1(x)y′+P0(x)y=f(x)

(7)

系数满足以下关系式

z(4)+c4z‴+c3z″+c2z′+c1z=f(x)/P5(P5≠0)

(8)

观察总结一般形式的三阶、四阶和五阶变系数线性微分方程可解条件的规律，可得n阶变系数线性微分方程可解的充分条件如下：

设一般形式的n阶变系数线性微分方程

Pn(x)y(n)+P(n-1)(x)y(n-1)+…+P1(x)y′+P0(x)y=f(x)

(9)

z(n-1)+cn-1z(n-2)+…+c2z′+c1z=f(x)/Pn(Pn≠0) (k=0,1,2,…,n-1;m=1,2,…,n)

(10)

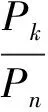
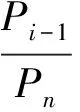
(2)在An(n+1)中：aij=0 (i>j)；ai(n+1)=ci-1-cicn-1(i=1,2,…,n)，规定cn=1,c0=0.

(3)由aij(i=1,2,…,n;j=1,2,…,n)构成一个n阶方阵Bn=(aij)n，该方阵关于副对角线对称.

(4)在Bn中:a1j=cn+1-j=a(n+1-j)n(j=1,2,…,n).

(5)Bn中的其余元素aij可由a(i-1)j和ai(j+1)确定.

根据Bn关于副对角线对称的性质，可设a(i-1)j=k1cm，ai(j+1)=k2cm,则有aij=(k1+k2)cm+1.

综上可知Bn为一个上三角矩阵，且ci(i=1,2,…,n)的系数排列满足杨辉三角形的规律.

按以上规律可直接得到六阶变系数线性微分方程可解的充分条件：

定理5：一般形式的六阶变系数线性微分方程

P6(x)y(6)+P(5)(x)y(5)+…+P1(x)y′+P0(x)y=f(x)

(11)

系数满足以下规律(k=0,1,2,…,4;m=1,2,…,6):

z(5)+c5z(4)+c4z‴+c3z″+c2z′+c1z=f(x)/P6(P6≠0)

(12)

据以上结论，可得到n阶变系数线性微分方程一个新的可解类型.

推论1：对于一般形式的n阶变系数线性微分方程

Pn(x)y(n)+P(n-1)(x)y(n-1)+…+P1(x)y′+P0(x)y=f(x)

(9)

当系数满足如下规律时：

3 例 题

例1求解下列方程

(13)

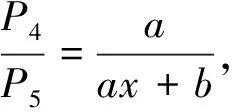
其中c1=1，c2=0,c3=2,c4=0,故方程(13)可解.

(14)

代入方程(13)中，可将原方程转化为

z(4)+2z″+z=kx+m

(15)

4 结束语

本文利用带导数的变量代换讨论了三阶、四阶和五阶变系数线性微分方程可解的充分条件，观察其中规律，最终得到了一般形式n阶变系数线性微分方程的一个新的可解类型.本文所做变量代换仅含有未知函数的一阶导数，在以后的研究中，作者会尝试利用带高阶导数的变量代换来处理三阶以及三阶以上的变系数线性微分方程，期望得到更多高阶变系数线性微分方程的可解类型.

参考文献

[1] 王建锋.求高阶常系数非齐次线性微分方程特解的新方法[J]. 数学的实践与认识,2007,37(12): 193-196.

[2] N.Г.彼得罗夫斯基著, 黄克欧译. 常微分方程[M]. 北京：高等教育出版社, 1957.

[3] 伍卓群,李勇译. 常微分方程[M]. 北京：高等教育出版社, 2005.

[4] 曹根牛.二阶变系数齐次线性微分方程与黎卡提方程[J].西安科技大学学报,2004,24(2): 247-249.

[5] 张学元.变系数二阶线性微分方程的一个新的可积类型[J].大学数学,2003,19(1): 96-98.

[6] 阎恩让.变系数二阶线性微分方程可解得充要条件[J]. 西安电子科技大学学报(自然科学版),2004,31(5): 796-802.

[7] 章联生.高阶变系数线性微分方程的一些新的可积类型[J]. 数学的实践与认识,2009,39(15): 229-234.

[8] 权大学, 赵临龙. 变系数二阶线性微分方程一个新的可解类型再讨论[J]. 大学数学,2007,23(3): 121-124.

[9] 赵临龙. 常微分方程研究新论[M]. 西安:西安地图出版社,2000.

[10] 王黎辉. 一类二阶变系数线性微分方程及其解的构造方法[J]. 大学数学,2006,22(5): 146-149.