通信信号盲源分离的高效算法研究
2011-02-20艾朝霞刘卫菠
艾朝霞, 刘卫菠
(1.榆林学院能源工程学院, 陕西 榆林 719000;2.西安电子科技大学通信学院, 陕西 西安 710071)
0 引 言
盲源分离的算法构造过程一般是首先选择恰当的代价函数,然后采用某种优化方法来搜索代价比函数的极值点,当代价函数达到极值点时各路源信号得到分离.按照优化方法的不同,可以将盲源分离算法分为自适应算法和批处理算法两类.自适应是盲源分离方法的一种重要的基本类型.自适应过程通常通过梯度来实现学习更新,其中自然梯度算法和FastICA算法是两种经典的自适应算法.
1 自然梯度算法和FastICA算法存在的问题分析
自然梯度算法[1,2]是随机梯度算法的一种改进算法,它是由信息极大化原理[2]推导出来的,自然梯度算法的自适应更新公式为:
W(k+1)=W(k)+μk[I-ψ(y(k))yT(k)]W(k)
(1)
FastICA算法[3,4]是建立在使提取信号的非高斯性最大化基础上的一种串行更新的自适应算法,该算法计算量小、收敛速度快,FastICA算法的迭代更新公式为:
(2)
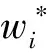
对于自然梯度算法,如果源信号数目是未知的,采用超定方式接收,则混合矩阵是m×n矩阵,分离矩阵为m×m方阵,此时输出的m路信号中除了存在n路源信号的拷贝外,还有m-n路冗余信号,它们是源信号的线性变换,通常以噪声的形式输出.这种情况下,互信息的极小值点并不是算法的平衡点,无法稳定收敛.另外,自然梯度算法需要源信号的概率密度函数估计,在噪声影响下或者源信号本身比较复杂的情况下无法很好地模拟(比如含复杂调制方式的通信信号),因此将自然梯度算法应用于通信信号的分离不能得到较满意的结果,特别是在低信噪比条件下,而且自然梯度算法本身有收敛速度较慢的问题,不适合对通信信号进行实时分离.
对FastICA算法,算法要求源信号为平稳的随机信号,对于非平稳或循环平稳随机信号,由于无法确定源信号的概率密度函数,从而无法对非线性函数做出相对合理的估计,导致算法性能下降.对于通信信号,大多数为数字调制信号,如ASK、MPSK、MQAM等,这些信号一般具有循环平稳性,无法对其概率密度函数做出准确的估计,如果用FastICA算法进行分离,性能将会严重下降.
2 自然梯度算法和FastICA算法的仿真分析
下面通过仿真实验对以上分析进行验证.在仿真中,选取如下4路源信号:2ASK调制信号、4FSK制信号(PM)、16QAM调制信号、256个子载波选用QPSK映射的OFDM信号.信号的采样点数为10 000个,首先用4跟接收天线进行接收,也就是适定情况下对信号进行分离.我们用性能指标串音误差对算法的收敛性进行分析,图1和图2分别给出了两种算法所对应的串音误差.
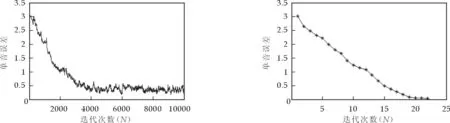
图1 自然梯度算法的串音误差 图2 FastICA算法的串音误差
串音误差表征了系统矩阵与理想情况单位矩阵的偏离程度,对于自适应盲源分离算法,从串音误差曲线可以清楚地看出算法在每一时刻的学习过程.由图1看出,自然梯度算法在处理过程中需要将近4 000次的迭代才接近收敛,可见其运算量很大,处理效率较低,不适合对通信信号进行实时分离.而FastICA算法仅需要20几次的迭代便可达到收敛,其运算量小,处理效率较高.
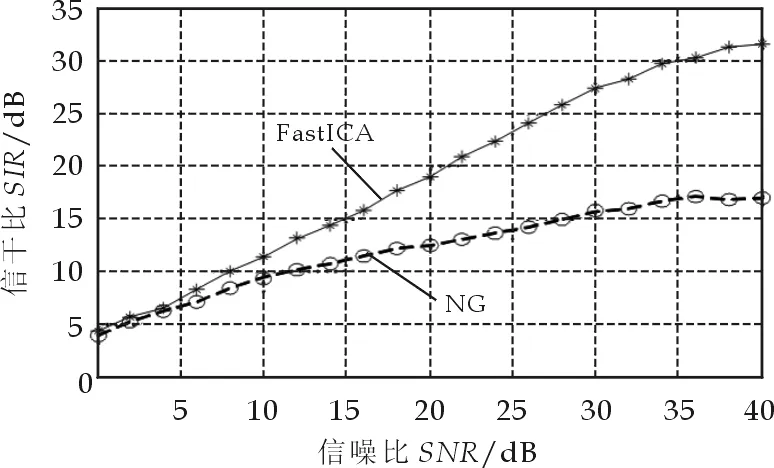
图3 两种算法信干比随信噪比变化的曲线
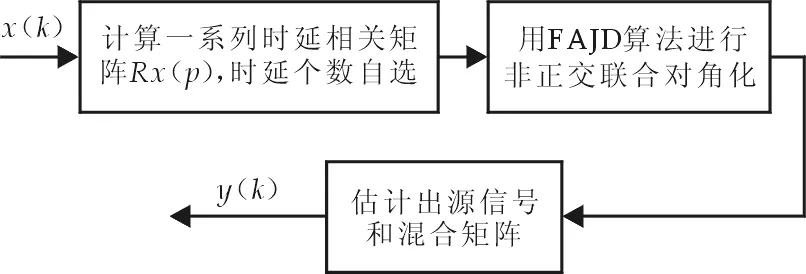
图4 基于二阶统计量非正交联合对角化算法的流程
如果用5根接收天线进行接收,即混合矩阵是一个的随机矩阵,这种超定情况下的盲分离如果采用自然梯度算法来进行,则经过仿真发现,算法在收敛一段时间后又重新趋于发散了,这说明自然梯度算法不能用于解决超定情况下的盲分离.
下面对两种算法的分离性能进行仿真分析,仿真条件不变,用信干比来衡量分离效果,图3表示了两种算法在不同信噪比条件下对接收信号进行分离的平均信干比,在每个信噪比条件下算法独立运行500次,然后取算术平均得到平均信干比.
信干比描述的是系统矩阵与理想单位矩阵的偏离程度,也即系统矩阵的系数程度,平均信干比越大,分离性能也越好.由图3可以看出,用两种算法对通信信号进行分离,FastICA算法的性能优于自然梯度算法.但是当信噪比较低时(<10 dB),两种算法的性能都不太理想.因此,对于通信信号,用传统的自适应算法分离不能得到理想的效果.
3 改进的基于非正交联合对角化的盲分离算法
联合对角化就是对于一组k个m×m目标阵列M={M1,…,Mk}(一般为方阵),寻求对角化变化矩阵V,使VTMkV均接近对角阵.联合对角化作为一种信号处理工具越来越引起了人们的注意,在盲源分离中也得到了非常广泛的应用,很多算法都引入了联合对角化来解决盲源分离问题,从而得到了各种联合对角化盲源分离算法.
基于正交联合对角化的盲源分离算法通常需要对混合信号进行预白化处理,而预白化处理会扰乱WLS准则,从而影响分离性能,降低算法的分离精度.基于此,非正交联合对角化[5-7]的概念被提出,由于非正交联合对角化方法中不要求变换矩阵V为正交矩阵,并且不需要预白化处理,因此非正交联合对角化算法具有更好的分离性能,我们采用一种改进的非正交联合对角化盲源分离方法[8].基于二阶统计量非正交联合对角化FAJD的盲源分离算法其处理框图如图4所示.
4 FastICA算法和FAJD算法仿真实验和性能分析
选取如下4路源信号:2ASK调制信号、4FSK制信号(PM)、16QAM调制信号、256个子载波选用QPSK映射的OFDM信号,其中每一路信号的具体参数设置如表1所示.
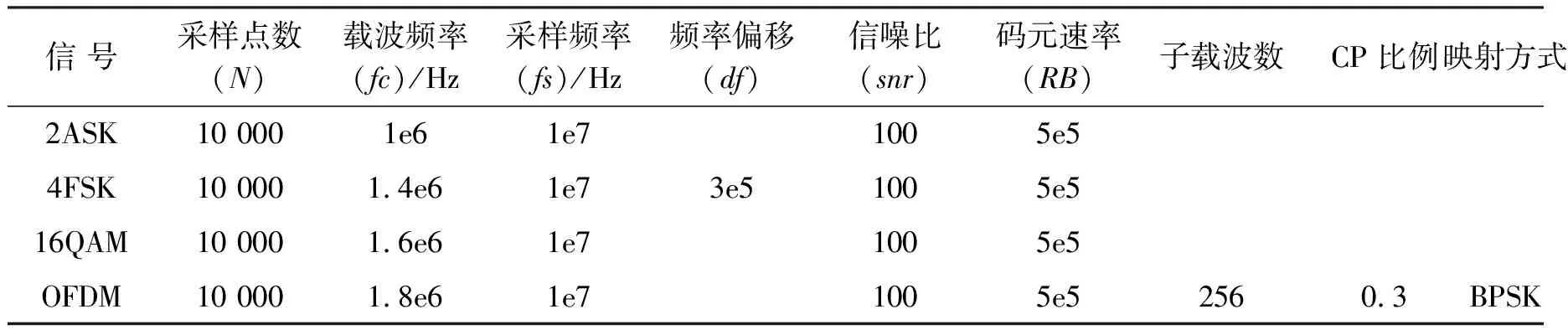
表1 各路源信号参数设置
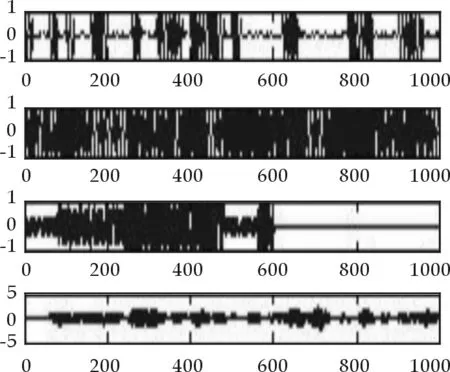
图5 4路源信号
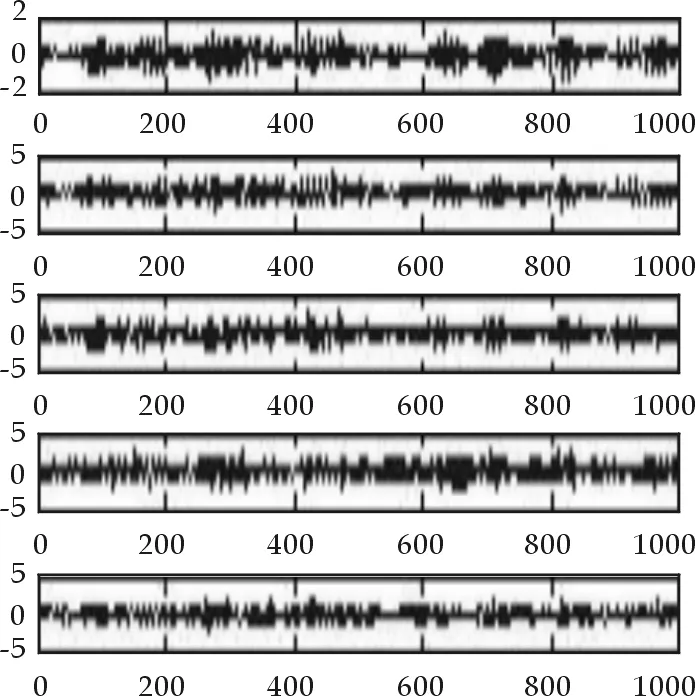
图6 5路混合信号
为了仿真证明在源信号数量动态变化时算法同样能将信号成功分离,在第三路16QAM信号前600个点加入信号,在600个点以后将信号去掉,每路信号取10 000个采样点,源信号波形如图5所示,为了便于观察比较,本文只画出了前1 000个点的波形.
为了仿真证明算法在超定情况下同样能够成功将信号分离,我们采用5根传感器接收,即混合矩阵为5×4随机矩阵,这样可以得到5路混合信号,在每一路混合信号中加入加性高斯白噪声,首先对每一路接收信号加入加性高斯白噪声,信噪比为25 dB,那么5路混合信号波形如图6所示.
用经典FastICA算法和FAJD算法进行处理分离后,仿真结果所得的分离输出波形如图7、图8所示.
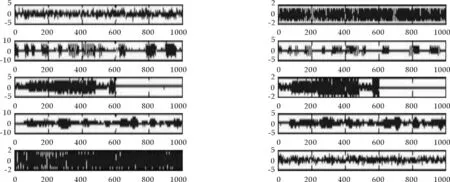
图7 FastICA算法分离输出信号图 图8 FAJD算法分离输出信号
仅从波形上,很难对算法的分离性能进行进一步的比较,为了更加量化地比较算法的性能,我们计算出信干比SIR来衡量算法性能.
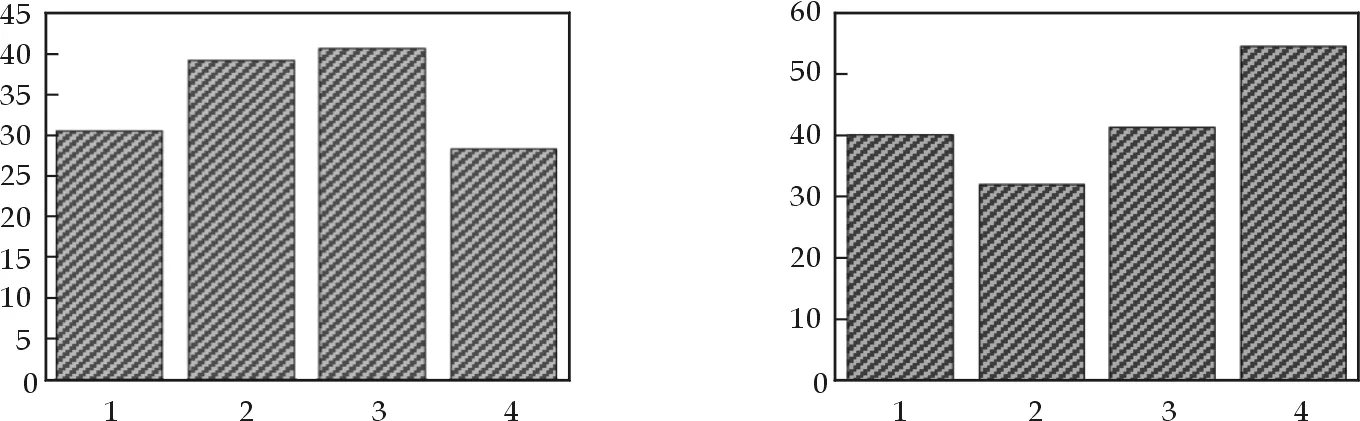
图9 FastICA算法的信干比SIR 图10 FAJD算法的信干比SIR
图9及图10中每一个柱图分别代表系统矩阵中对应的一对源信号与分离输出的一行信号的信干比,具体意义是该行最大元素的平方与其它元素的平方和的比值,该比值越大就代表该行越稀疏,系统矩阵的该行就越接近理想情况,恢复的信号受其它信号的干扰就越小.通常对每行的信干比求平均值,称为平均信干比,用平均信干比来衡量算法的整体性能,平均信干比越高,算法性能就越好.
从以上对比看出,在信噪比为25 dB的噪声背景下,FastICA算法和改进的非正交联合对角化FAJD算法都能成功地实现通信信号的盲分离任务.但是,改进的非正交联合对角化算法比FastICA算法的信干比更高一些,因此改进的非正交联合对角化FAJD算法比FastICA算法具有更好的分离性能.

表2 不同信噪比下两种算法的平均信干比
把信噪比降为20 dB,15 dB,10 dB,重复做上面的仿真实验,同样显示采用改进后的FAJD算法比FastICA算法处理的性能有明显提高.在信噪比降为10 dB时,改进后的FAJD算法的盲分离结果虽然没有高信噪比情况下那么理想,但仍然可以实现源通信信号的盲分离任务.
为便于更直观地比较两种算法的分离性能,用表2记录了对上述各仿真实验分别独立运行200次然后取平均后所得的平均信干比,通过观察表中所记录的平均信干比的变化情况,就可清楚地看出改进后的FAJD算法在低噪声环境下分离性能显著提高.
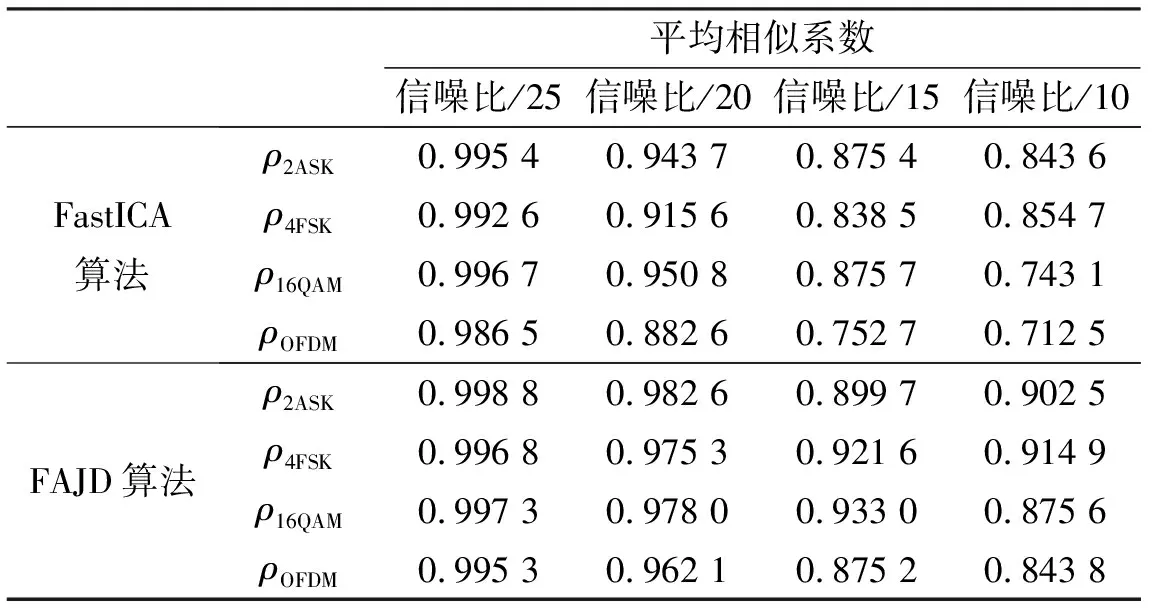
表3 不同信噪比下两种算法的平均相似系数
下面再以相似系数作为评价指标,对两种算法进行比较.两种算法在不同信噪比下的平均相似系数如表3所示.
表3进一步证明了改进的非正交联合对角化FAJD算法比FastICA算法具有更好的盲分离性能,尤其是在低信噪比背景下,改进的非正交联合对角化算法仍然能够实现数字调制通信信号的盲分离任务.
5 结束语
自然梯度算法和FastICA算法在处理通信信号时存在分离性能低和收敛速度慢的问题,本文用非正交联合对角化方法对其进行了改进,给出了基于FAJD的盲源分离算法,能够针对复杂数字调制方式的通信信号且信号数目未知且动态变化的情况下,在可接受的噪声范围内,采用超定方式,实现有效的分离.仿真结果表明,改进的算法在低信噪比条件下的分离性能有明显的提高.
参考文献
[1] Bell A J, Sejnowski T J. An information-maximization approach to blind separation and blind deconvolution[J]. Neural Computation,1995,7(6):1 129-1 159.
[2] Amari S. Natural gradient works efficiently in learning[J].Neural Computation,1998,10(2):251-276.
[3] Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Trans Neural Networks,1999,10(3):626-634.
[4] Hyvarinen A, Oja E. Independent component analysis:algorithms and application[J]. Neural Computation,2000,(13):411-430.
[5] Vollgraf R and Obermayer K. Quadratic optimization for simultaneous matrix diagonalization[J]. IEEE Trans Signal Process,2006,54(9):3 270-3 278.
[6] F WANG, Z LIU, J ZHANG. Nonorthogonal joint diagonalization algorithm based on trigonometric parametrization[J]. IEEE Trans. Signal Process,2007,55(11):5 299-5 308.
[7] Petr Tichavsk and A.Yeredor. Fast approximate joint diagonalization incorporating weight matrices[J]. IEEE Trans. Signal Process,2009,57(3):878-891.
[8] Xi-Lin Li, Xian-Da Zhang. Nonorthogonal joint diagonalization free of degenerate solution[J]. IEEE Transactions on Signal Processing, 2007,55(5):1 805-1 808.
