一种板形特征点运动补偿模型的研究与实现
2011-02-20张艺钟韩俊强
杨 林, 张艺钟, 韩俊强
(1.西安市特设检验研究院, 陕西 西安 710068; 2.西安交通大学计算机系, 陕西 西安 710049)
0 前 言
运动中板形平直度的测量是板材矫直技术中的研究热点[1-4].本文根据图像局部特征和运动补偿等相关理论提出了一种板材特征点运动补偿模型,该模型以视频连续图像帧为输入,计算出对当前图像帧进行运动补偿的相关数据.
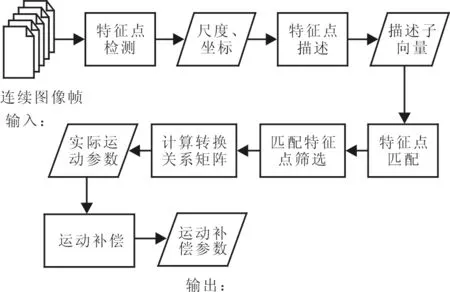
图1 板形特征点运动补偿模型工作流图
1 板形特征点运动补偿模型
板形特征点运动补偿模型的工作流是一个按顺序运行的处理过程,如图1所示,包括:视频连续图像帧的特征点检测;使用描述子对检测到的特征点进行描述;对连续图像帧的特征点计算匹配度;建立转换关系矩阵;计算运动补偿数据等.
(1) 视频连续图像帧序列经过图像预处理过程转化为该模型的输入数据,使用特征点检测子定位图像帧的特征点并采用SIFT描述子算法将其定量化描述.
(2) 运用欧氏距离在图像帧的描述子向量集合之间计算特征点匹配对,即建立后续处理过程中所需要输入的特征点匹配对.
(3) 基于特征点对建立相应的映射方程,计算图像帧间的转换关系矩阵并将其代入运动补偿模型以获得对当前图像帧的运动补偿数据.
2 特征点检测和描述算法
使用DoG检测子对板形视频连续图像帧进行特征点的检测,其步骤如下:
(1) 建立高斯差分金字塔. 对原图进行高斯处理得到高斯差分图:
D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]×I(x,y)=L(x,y,kσ)-L(x,y,σ)
(1)
图2 主方向计算
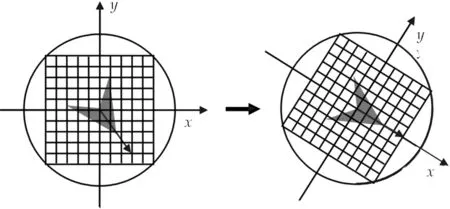
图3 主方向旋转
(2) 原图特征点的计算. 在高斯差分图像中查找局部极值点时,选中某一点所在的图像域中的周围8个点和相邻两个尺度图像中的9×2个点相比较确定该点是否为极值点,即在选中的26个点中判断该点是否为最大值或最小值点.
(3) 对特征点进行精确定位. 使用曲线拟合和Hessian算法,计算主曲率并对检测到的点进行低对比度点和边缘点的确定与去除工作.
当找出特征点之后使用SIFT描述算法对其进行描述,SIFT描述子生成过程如下:
① 确定特征点主方向. 如图2所示,在检测到的特征点所在的尺度空间中以该特征点为圆心,3×1.5×σ为半径的邻域内使用统计梯度值的方法获取特征点的主方向.
(2) 生成特征点描述子. 如图3所示,以主方向和其正交方向为新坐标系,统计特征点邻域内的梯度幅值,即对主方向进行旋转.
特征点的新坐标与原坐标的对应关系为:
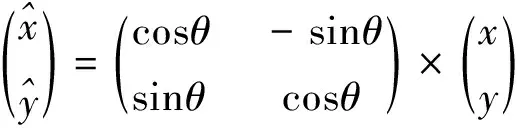
(2)

一般以8个方向为一组统计梯度值并得到描述子向量.以2×2×8SIFT描述向量的产生过程,如图4所示.
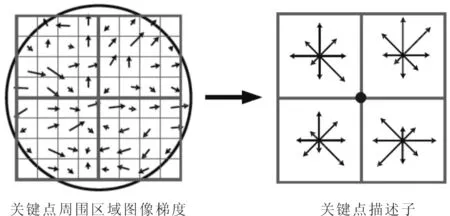
图4 描述子生成过程
3 Kalman算法及其改进
Kalman算法的原理式来自于贝叶斯公式.首先通过前一状态得出当前状态的预测值,再采用当前观察到的状态值,对其进行处理并得出最终的值.在板形测量中Kalman算法用于从连续图像帧转换关系矩阵中去除因板材自身不规则运动而带来的干扰,即得出运动补偿所用的数据.
使用第1小节中被检测和描述的特征点建立连续图像帧间的转换关系:
(3)
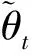
从式(1)可以进一步得出板形连续图像帧在理想情况下的转换关系,即无干扰情况下的转换关系:
It=AIt-1+Ut
(4)
其中A表示图像帧在理想状态下的转换关系,It表示t时刻理想的板形状态值,Ut表示白色噪声.同样可以推导出板形观测值的状态转换关系,即带不规则运动的板材状态转换关系:
St=HSt-1+Vt
(5)
其中H表示图像帧间的转换关系,St表示t时刻的板形状态值,Vt为白色噪声,与Ut相互独立.将板形观测值St视为板形理想值It的带干扰版本.
(6)
其中“-”和“+”分别表示先验值和后验值,Kt是Kalman增益值.
现在的问题是通过特征点检测得出的特征点对数量较为充足,如何从大量的特征点对中选取适合计算的原数据.如果全部加入计算那么将会影响整个系统的运行效率,而将部分特征点对参与运算,则可能会丢失一些表示连续图像帧之间转换关系的重要信息.针对这一问题,本文进行以下优化.
每对匹配特征点都包含了一定信息量的相邻图像帧间的转换关系,但不同特征点对之间所包含的信息量不同.对于转换关系的计算有些特征点对尤为重要,而有些特征点对的影响则可忽略不计.在本文中将特征点坐标代入2×2的系数矩阵[5,6]计算特征值从而决定其权值,该矩阵为:
(7)
其中(px,py)表示在坐标(x,y)处的坐标值,ws和wy表示特征点邻域的高斯计算窗口,Ix(x,y)和Iy(x,y)分别表示特征点在水平方向和垂直方向的梯度值.下面分析采用该矩阵的原因:
高斯窗口中邻域点与特征点的灰度差的平方值E(u,v)可表示为:
(8)
其中w(x,y)表示高斯窗口,u,v表示邻域点与该特征点在x坐标和y坐标的距离.为了获得任意方向的灰度差,将式(8)通过泰勒公式展开得出:
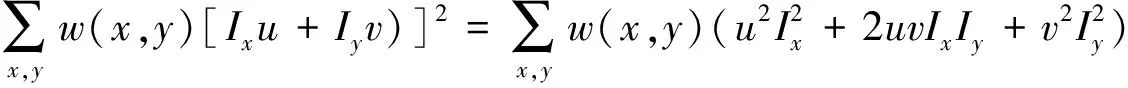
(9)
其中Ix表示x方向偏导,同理Iy表示y方向偏导.将式(9)写成矩阵形式:
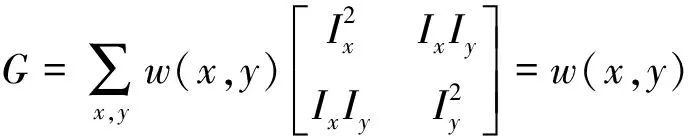
(10)
其中⊗表示卷积,将式(10)代入式(9)得:
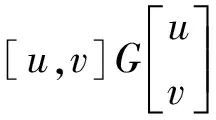
(11)
从式(11)发现灰度差E(u,v)的大小与矩阵G有关,因此可通过判断矩阵G的特征值来判断该点是否为特征点,进一步可以计算该点的权值,如图5所示.
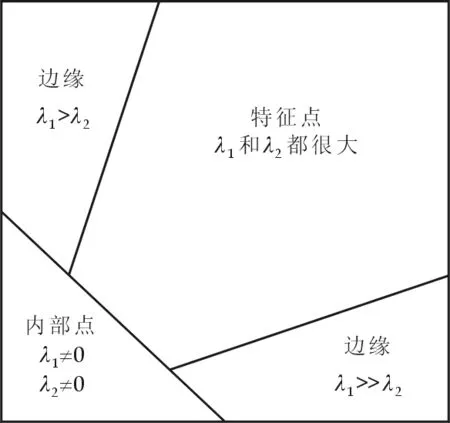
图5 特征点权值的确定
从图5可知当该矩阵中两个特征值都很大时可以判断该点为特征点,因此其对应的权值也可以由特征值确定.
4 结果分析
为了衡量预测值的准确性,我们采用均方根误差(Root Mean Square Error ,RMSE)作为误差衡量标准,其表达式如下式所示:
(12)
在本实验中从板材连续图像帧序列中随机选取包含10、15、20、25和30个图像帧的图像序列,分别使用改进前和改进后的Kalman模型进行运动估计处理,获得的实验数据如表1所示.
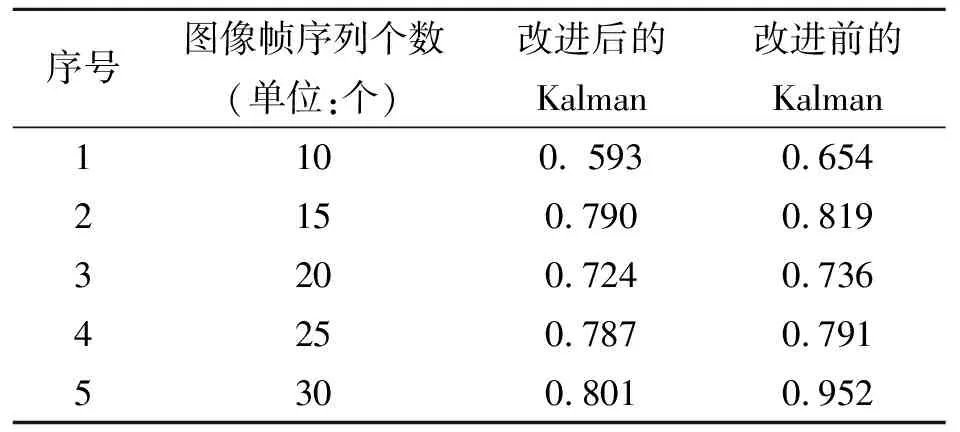
表1 改进前后的Kalman算法均方根误差的比较
从表1中可以看出改进后的Kalman模型对运动估计的准确度与改进前的Kalman模型相比较有了较大的提高,而且随着图像帧序列个数的增加其运动估计性能还能保持较高的精度.
5 结束语
本文中的特征点运动补偿模型是在图像特征点检测、描述的基础上使用Kalman算法计算出对当前图像帧进行运动补偿的数据,在本模型中针对Kalman 算法的特征点筛选过程进行了改进,并在保证该模型实时性的基础上满足了精确性要求.
参考文献
[1] 刘 凯,徐宏喆.板材矫直机智能控制及应用[M].北京:机械工业出版社,2010.
[2] 杨光辉,张 杰,曹建国,等.一种新的带钢平坦度在线检测方法的研究[J].冶金设备,2006,(3):51-54.
[3] 王向丽 ,李谋渭.张力计的辊高差对板形检测精度的影响[J].北京科技大学学报,2010,32(8):29-32.
[4] Scottow C.Shape measurement and coolant spray solutions for rolling mills[J]. MPT Metall Plant Technol Int,2008,25(1) : 72.
[5] C. Tomasi, T. Kanade. Detection and tracking of point features[R]. Carnegie Mellon University Technical Report CMU-CS-91-132, 1991.
[6] J.-Y. Bouguet. Pyramid implementation of the Lucas Kanade feature tracker: description of the algorithm[R]. Intel Corporation, Microsoft Research Labs Technical Report,2000.
