基于距离比阈值参数自适应的SIFT算法研究
2011-02-20王泽梁汪道寅汪丽华
王泽梁, 汪道寅, 汪丽华
(1.合肥工业大学计算机与信息学院, 安徽 合肥 230009; 2.中国科学技术大学电子工程与信息科学系, 安徽 合肥 230027; 3.黄山学院信息工程学院, 安徽黄山 245041)
0 引 言
David Lowe提出的尺度不变特征SIFT算法具有尺度、旋转、仿射和光照等不变性的特征[1].SIFT算法主要可分为3部分:特征检测、特征描述和特征匹配.特征检测是在图像上对特征进行提取,特征描述是对特征进行表达,特征匹配则是对特征进行配对.Mikolajczyk和Schmid通过对比SIFT、PCA-SIFT、steerable filter、moment invariants等数十种特征描述后指出[2,3],SIFT是目前最为有效的特征检测算子.SIFT算法因其优异的性能得到了相关领域学者的广泛关注,陆续出现了一些变种算法,如Yan Ke在2004年提出的PCA-SIFT算法[4]、Mikolajczyk等在2005年提出的GLOH(Gradient Location Orientation Histogram)算法[3]、Bay在2006年提出的SURF(Speeded Up Robust Features)算法[5]、Guoshen Yu 和Jean在2009年提出的ASIFT算法[6]等.SIFT算法仍存在需要完善的地方,如检测到的特征点不具有均匀性分布,检测步长不能进行动态调整等.针对以上问题作者研究并提出了相应的均匀性特征检测和动态步长的设计方法,实验表明改进算法能够实现更有效的图像配准.
1 SIFT算子简介
1.1 检测尺度空间的特征点
高斯卷积核是实现尺度变换唯一的线性变换核,一幅图像在尺度空间中的表示为图像和可变高斯核函数的卷积,LoG(Laplacian of Gaussian)算子表达式如下:
L(x,y,σ)=G(x,y,σ)⊗I(x,y)
(1)

D(x,y,σ)=G(x,y,kσ)-G(x,y,σ)⊗I(x,y))=L(x,y,kσ)-L(x,y,σ)
(2)
其中,因子k满足k=21/S.将D(x,y,σ)在尺度空间中的极值点作为候选特征点.
1.2 精确定位特征点的位置
通过拟和三维二次函数以精确确定特征点的位置和尺度,同时可去除低对比度的关键点和不稳定的边缘响应点,以增强匹配的稳定性.差分金字塔DoG的泰勒展开式如下:
(3)
其中,X=(x,y,σ)T为包含特征点位置和尺度信息的向量.由差分金字塔DoG的幅值大小及曲率来剔除低对比度点和边缘响应点.
1.3 确定特征点的主方向
坐标为(x,y)的关键点其梯度幅值和方向分别为:
(4)
θ(x,y)=tan-1((L(x,y+1)-L(x,y-1))/(L(x+1,y)-L(x-1,y)))
(5)
在以特征点为中心的邻域窗口内用梯度方向直方图来统计邻域像素的梯度方向.梯度方向在0°~360°,其中每10°在直方图中表示一个柱,共36柱.梯度方向直方图的峰值代表了该特征点处邻域梯度的主方向,即作为该特征点的主方向.
1.4 生成特征描述符
以特征点为中心取16×16的窗口(特征点所在的行和列不取),每个小格代表特征点邻域所在尺度空间的一个像素,采用高斯加权(越靠近特征点的像素,梯度方向信息贡献越大).在4×4的图像小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,形成一个种子点.梯度方向直方图统计公式[7]如下:
(6)
其中,ck为方向柱的中心,Δk为方向柱的宽度,(x,y)为子块r(l,m)像素点的坐标.
一个特征点由4×4共16个种子点组成,特征描述子由所有子块的梯度方向直方图构成:
u=(hr(1,1),…,hr(l,m),…,hr(4,4))
(7)
因此,最终形成128维的SIFT特征向量即作为SIFT算法的特征描述符.
1.5 特征点之间的匹配
通过计算128维的特征描述符之间的Euclid 距离来度量2 个特征点之间的匹配程度.当2 个特征描述符的Euclid 距离最小并且与次最小 Euclid 距离的比值小于给定的阈值0.8时,则这2个特征点满足匹配关系.

图1 欧氏距离比的概率密度分布
2 距离比阈值参数的自适应方法
欧氏距离比|DA-DB|/|DA-DC|表示最近邻欧氏距离和次近邻欧氏距离之间的比值,当该比值在一定的阈值t范围内时则认为最近邻欧氏距离所对应的一对特征点是匹配特征点.
David给出的距离比概率密度分布[1]如图1所示,其中实线为正确匹配点的概率密度分布,虚线为错误匹配点的概率密度分布.由图1可以看到,David将距离比阈值参数设为0.8是合理的,此时虽然损失了5%的正确匹配点,但同时将减少90%的错误匹配点.然而图1并不能反映所有图像的欧氏距离比概率密度分布,也即这种固定阈值的方法并不是十分合理的方法.在对不同的图像进行试验时,阈值并不总能得到最佳效果,因此参数并不是对所有图像均有效.一个有效的算法应当使得阈值参数具有尽可能高的鲁棒性,能够满足不同情况需要.为此,应对不同的图像自适应调整阈值,使特征点能够更准确地实现匹配.

图2 参考图像和待配准图像

图3 参考图像和待配准图像的特征点分布
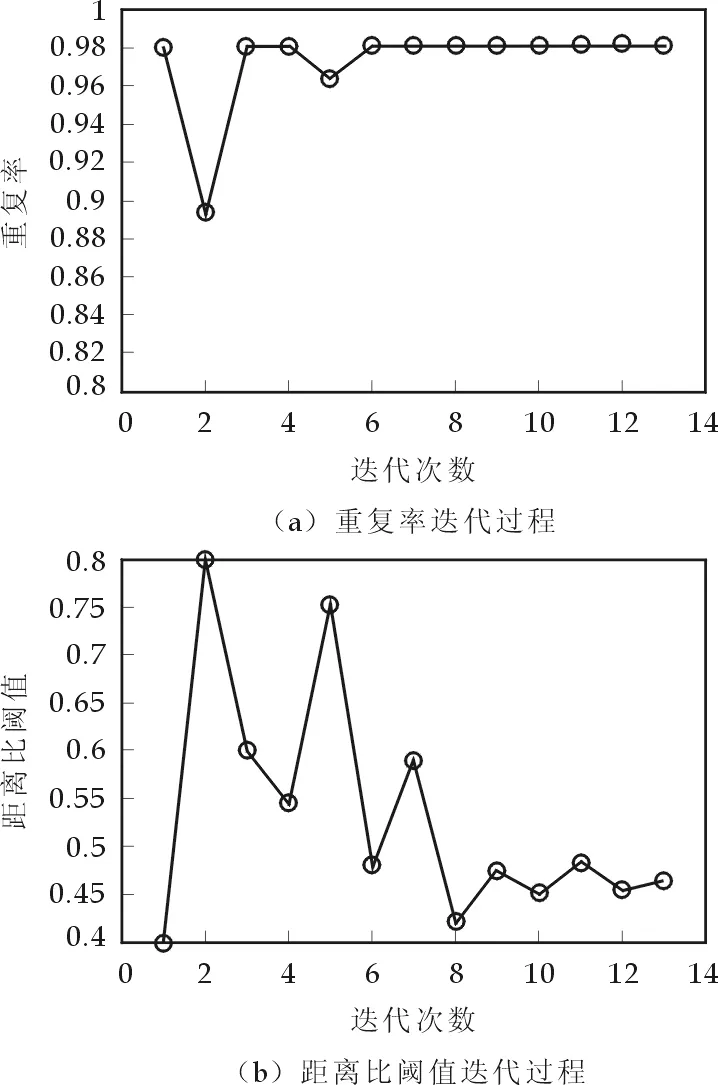
图4 重复率与距离比阈值迭代过程
为选择一个最优的欧氏距离比阈值参数,需要在算法实现中加入参数寻优的过程,参数是否最优通过重复率进行衡量.重复率越大,表明匹配程度越高,欧氏距离比阈值的选取越合理;重复率越小,表明匹配程度越低,欧氏距离比阈值的选取越不合理,需要重新进行选取.但是重复率与欧氏距离比阈值之间并不存在明确的函数关系式,这给寻优过程带来了麻烦.通过大量实验表明,欧氏距离比阈值的取值范围在[0.4,0.8]之间比较合适.阈值取的太大,则表明匹配的要求太宽泛,错误匹配的点将增多;阈值取的太小,则表明匹配的要求太严格,正确匹配的点将减少.目前已经产生了很多的智能优化方法,如参数少、计算简单的粒子群(Particle Swarm Optimization,PSO)算法,还有遗传算法(Genetic Algorithm,GA)、蚁群算法(Ant Colony Algorithm,ACO)等.考虑到只对欧氏距离比阈值参数进行寻优且已知参数的优化范围,故不需要引入优化方法,可以采用最为基础的折半查找法进行寻优即可.具体过程如下:
(1)设待优化参数的取值区间为[a,b],区间的中间值为c,初始值a=0.4,b=0.8,c=0.6,l=0.2.计算a,b,c所对应的重复率R(a),R(b),R(c),M=max(R(a),R(b),R(c)).
(2)在c的左右生成两点d=c-l*rand和e=c+l*rand,计算d,e所对应的重复率R(d)和R(e)(其大小必须大于M,否则重新生成d,e),比较两者大小.
(3)若R(d)>R(e),则M=R(e),l=l/2,a不变,b=c,c=c-l,返回步骤(2);若R(d) (4)当两次M的差值小于0.01或者达到最大搜索次数50时,算法终止. 上述过程中,若出现M为1的值,则算法立即终止,不需要再继续搜索,对应的距离比阈值作为所求参数.由于匹配运算占SIFT算法中的运算比例很小,所以以上寻优不会给SIFT算法带来太大的运算负担. 实验以典型的Lena图像为例,图2(a)以131×131大小的Lena图像作为参考图像,图2(b)为图2(a)旋转30°后形成的大小为179×179的待配准图像. 参考图像共检测到126个特征点,待配准图像共检测到162个特征点,检测结果如图3所示.对检测到的特征点生成特征描述子时,描述子的位置和特征点的位置一致. 图5 距离比阈值与重复率的关系曲线 图4给出了欧氏距离比阈值参数的寻优过程.其中,图4(a)代表重复率的迭代过程,图4(b)代表距离比阈值参数的迭代过程.通过前面的寻优算法,距离比阈值参数和重复率不断寻优,直到最大重复率和最优距离比阈值.算法共进行了13步迭代,重复率最终取0.981 1,距离比阈值参数最终取0.464 1.由图4可以看到,距离比阈值参数通过不断迭代、折半缩小区间的方法最终得到了所需要的取值. 通过距离比阈值参数的寻优,得到了该图像下的最佳距离比阈值参数,距离比阈值与重复率的关系如图5所示.由于算法利用了折半查找思想,在阈值区间已知的情况下能够较快地找到最优参数,因此不会带来大的运算量. 距离比阈值参数对不同的图像其值的选取是不同的,并且具有不同的分布,所以应该针对不同的图像进行选择.距离比阈值参数有时的取值并不是某个特定值,而是在一定区间取值均可,如上图所示. 尺度不变特征SIFT算法因其稳定性、独特性和多量性等优点,对图像处理领域发挥着越来越重要的作用.本文在SIFT算法的匹配阶段对距离比阈值进行自适应动态调整,使其满足不同图像的需要.实验表明,基于折半查找法思想的寻优能够找到最优的距离比阈值,同时不会产生太大的运算量.后续工作将对不同类型的图像进行更多实验和比较、设计更有效的特征描述子,并将算法应用到实际当中去. 参考文献 [1] DAVID L G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [2] Mikonaiczyk K, Schmid C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10):1 615-1 630. [3] Mikolajczyk K, Schmid C. A performance evaluation of local descriptors[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 2005, 27(10):1 615-1 630. [4] Ke Y, Sukthankar R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors[C]. Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 2004: 511-517. [5] Bay H, Tuytelaars T, Gool L V. SURF: Speeded up Robust Features[C]. European Conference on Computer Vision, Springer-Verlag, Berlin, Heidelberg, 2006: 404-417. [6] Morel J M, Yu G S. ASIFT: A new framework for fully affine invariant image comparison[J]. Society for Industrial and applied Mathematics Journal on Image Sciences, 2009, 2(2): 438-469. [7] Mikolajczyk K, Schmid C. Scale and affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63-86.3 实验结果及分析
3.1 匹配图像的选取
3.2 特征的检测和描述
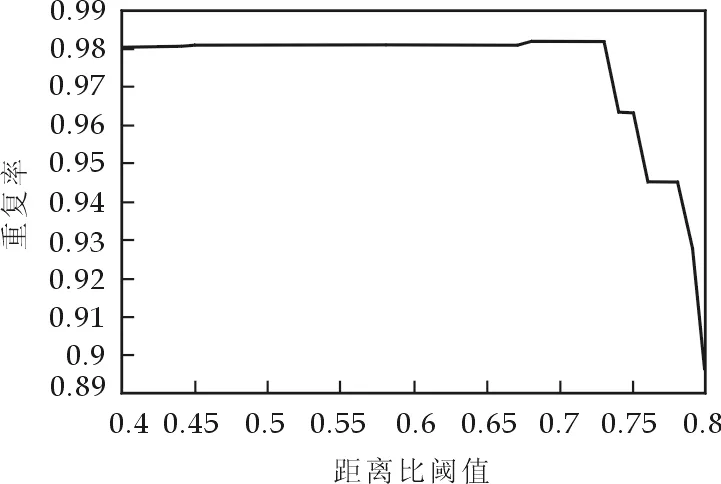
3.3 距离比阈值参数自适应
4 结束语
