基于随机振动响应互相关函数的结构损伤识别试验分析

雷家艳，姚谦峰，雷 鹰，刘 朝

(1.北京交通大学 土木建筑工程学院，北京 100044;2.厦门大学 建筑与土木工程学院，福建 厦门 361005)

结构动力损伤识别的研究近年来取得了较快的发展［1，2］。损伤识别的思路大多是通过时域及频域的分析方法识别结构的模态参数(频率、振型)，或通过结构模态反演获得结构的物理参数(如刚度等)，在此基础上对比结构损伤前后的频率、阻尼、模态振型、柔度(刚度)矩阵、应变能等参数，构造损伤因子对结构损伤的位置及程度进行识别。在识别过程中，这些思路存在结构损伤前后的频率变化不敏感、模态振型的识别有限且精度不高、大型工程结构的模态参数矩阵到物理参数矩阵的动力反演过程较复杂等问题，使这些方法在实际工程中的应用受到一定的限制。

因此，利用结构随机振动的动力实测数据进行损伤检测具有重大的现实意义。此类方法一般不需要测得外激励，通常只要求外激励的频谱特性相对稳定，对于结构通常所受的环境激励及常规使用荷载而言，均能满足这一要求。另外，基于随机振动响应的互相关分析能有效避免测试噪声对响应信号的污染。因此，文献［5，6］提出的以互相关函数为基础的结构损伤识别方法是可行的。该方法定义了以某一基点为参照点的结构响应互相关函数幅值向量CorV概念，并参照模态置信度判据的定义，构造了相关函数幅值向量置信度判据CVAC，利用CVAC随损伤程度的增大而单调下降的特性，可判定损伤是否存在，再对结构损伤前后的CorV进行差分，使相关函数幅值向量在损伤位置处凸显，从而实现损伤的定位。文献［7，8］在前者互相关函数幅值向量的基础上，结合小波变换或内积向量对结构进行损伤检测同样取得很好的结果。相对于对比结构的频率、阻尼、模态振型、柔度(刚度)阵、应变能等参数的变化，利用结构在随机激励下动力响应的互相关函数进行结构损伤识别的方法具有明显优势，此类方法直接以结构损伤前后测点响应(位移、速度、加速度)的互相关函数构造识别参量，使得结构的损伤检测更加简便。但是，从已有文献中的识别例子可见，对于大型结构(如大跨径桥梁、多高层房屋建筑)的识别需要布设足够多的测点，同时测得众多测点的振动响应以建立具有识别意义的识别判据，应该是比较理想的方法，但在实际检测过程中，由于经济等因素的制约，这是较难实现的。另外，在利用互相关函数进行损伤程度量化方面还有待进一步研究。本文在随机振动互相关函数的基础上，以相邻测点的动力响应时程为基础，定义了新的互相关函数幅值向量R和损伤因子K，通过试验数据分析表明，对结构损伤的定位及量化是可行且有效的，并通过CVAC等特性分析，提出了结构在线监测及分散检测的思路。

1 互相关函数用于结构损伤识别的依据

1.1 互相关函数幅值向量的定义

互相关函数描述了随机振动过程中两个样本函数在不同瞬时幅值之间的依赖关系，它可以反映两条随机振动信号波形随时间坐标移动时相互关联的紧密性［3］。结构在随机振动下(如地震、风作用、交通荷载及其他随机激励)，两相邻测点的响应可视为两个实平稳随机过程x1和x2，它们之间的互相关函数为:

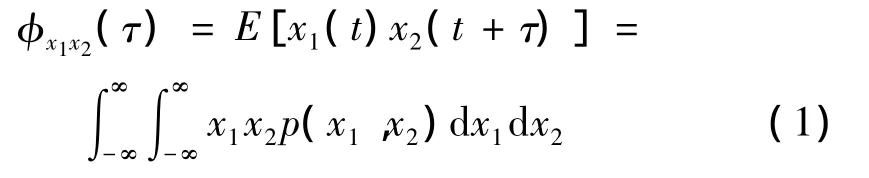
假定随机振动响应满足各态历经性，互相关函数可用单个样本的时间历程来平均，即:

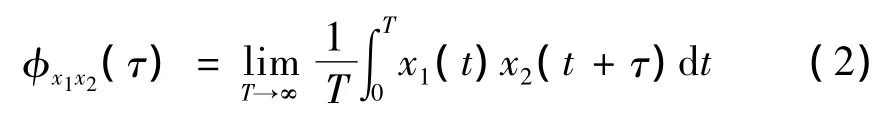
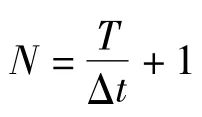
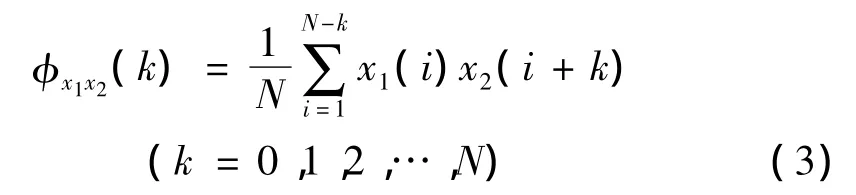
定义两相邻测点间的互相关函数幅值为:

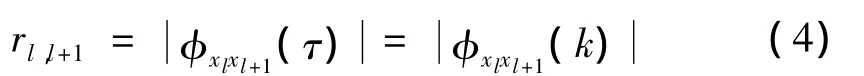
如果结构上同时布设了n个测点，计算各相邻测点响应时程的互相关函数幅值，即形成向量:

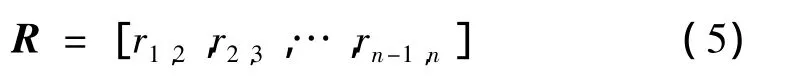
在已有文献［5，6］中提出了以某一测点为参考点的互相关函数幅值向量，根据本文定义使用的符号可表示为:

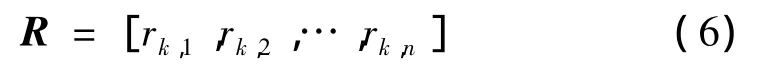
公式(5)与公式(6)相比，由于没有基点k的牵制，它对损伤的局部反映更直观。而且，对于大型结构，可根据结构特点进行分区域的分散式检测，而无需对整个结构同时布测点进行整体式检测。

当随机振动外部作用力的频谱范围变化不大时，互相关函数幅值向量的形态就会相对固定［4～9］，将任意时段相邻测点振动响应的互相关函数幅值向量与基准时段的幅值向量形态作对比，形态突变的地方即为损伤位置。因此，幅值向量R的变化，即可作为是否存在损伤的初步判据，同时也兼有损伤定位的功能。这在后面的试验分析中将会得到验证。

1.2 损伤因子的构建

损伤因子是结构损伤识别的量化核心，参照相关函数幅值向量置信度判据CVAC的定义［5，6］，将损伤因子定义为:

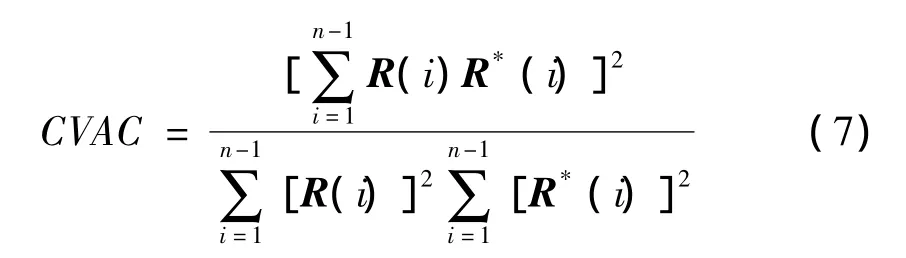
式中R(i)，R*(i)分别表示损伤前后相邻测点的相关函数幅值向量。理论上CVAC的取值范围为［0，1］，无损伤时CVAC=1，完全损伤时(如完全断裂)CVAC=0。已有的文献［5，6］及本文第2节实验数据分析的结果表明，尽管互相关函数幅值向量在一定条件下可视为一种“广义模态”［7，8］，但参照模态置信度准则构造的CVAC与损伤程度之间不能形成单一的映射关系。这就需要建立新的损伤程度判据。

损伤情况相同，且外激励频谱范围一定时，不同激励下所有的互相关函数幅值向量曲线形状相似，即曲线形态是固定的，仅会因外激励幅值大小的变化而产生上下平移，可用公式(6)对R再进行归一化处理，新的向量R1使损伤的识别更加简洁。

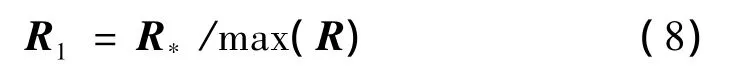
若在测点i与i+1的结构区段发生损伤，与无损情况相比，幅值向量会在损伤位置处出现向量因子突变，以突变程度作为损伤程度的量化依据，将结构损伤因子K定义为如下表达式:

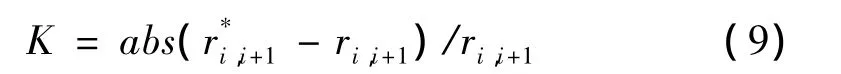
1.3 识别“盲区”的处理

由于互相关函数幅值的定义是以相邻测点响应为基础的，在最外侧测点以外的结构区段，由于测点的缺失而无法对这些区段进行损伤检测，即形成识别“盲区”。第3节中的八层剪切框架，由于底层柱端约束近似为刚接，测点布置在每层楼板处，导致底层框架区段的向量因子r0，1缺失，从而出现了约束边界段的“盲区”问题。

这样，为使结构的检测全面，对于识别“盲区”的处理只能采取测点加密或最外测点尽量外延的方法尽量缩小“盲区”区段。

1.4 检测方法的抗噪能力

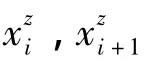
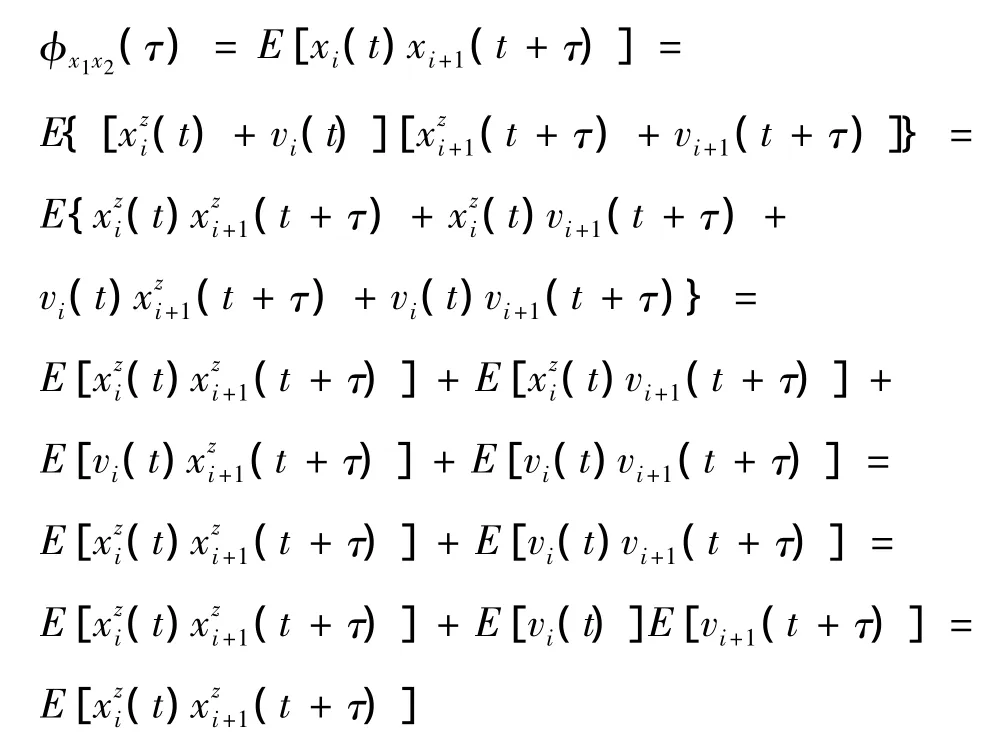
由前面的假定可知，以相邻测点实测响应为基础计算的互相关函数收敛于真值。

2 试验分析

2.1 试验概况

试验模型为一剪切型八层钢框架结构，如图1。每层框架平面边长为350 mm×250 mm，层高为200 mm。框架底部用螺栓锚固在地上，节点连接采用双排螺栓，可近似地认为框架连接为固结。结构损伤表现为某层间侧向刚度的减少，试验中通过变换不同重量的钢柱片模拟刚度的降低。激振点位于第三层框架处，振源是利用RIGOL公司生产的DG-1022信号发生器产生的白噪声激励。拾振设备采用PCB传感器，试验中只采集加速度响应时程，不考虑速度及位移时程。采样频率设为100 Hz。

图1 试验模型及加载设备Fig.1 Test model

试验共分为四组进行，分别模拟以下情况:(1)无损伤;(2)第六层框架发生25%的损伤;(3)第六层框架发生50%的损伤;(4)第四、六层均发生25%的损伤。为分析不同激励下识别方法的有效性，每组试验通过调节信号发生器的电压值，分别采用了五条不同的白噪声激励。试验前5秒尚未施加激励，信号记录为单纯的环境噪声，因此，测试数据以此时刻开始。测试得到的时程信号经标定变换、消除多项式趋势项、数字滤波等信号预处理后再进行有关计算，采样数据预处理前后的对比如图2。

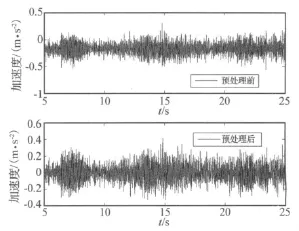
图2 采样数据预处理前后对照Fig.2 Comparison of signals between tested and preprocessed

2.2 损伤定位分析

如表1所示，框架无损伤时，以五种激励作用下的响应计算得到的CVAC值由于试验模型、实测噪声等因素的影响，以极小的误差近似等于1，与理论值几近吻合。另外，结构发生同一种损伤的情况下，以不同激励下的动力响应时程为基准状态计算得到的CVAC值也近似为1。这表明，CVAC可作为同类损伤实测数据可靠性的判断标准。同时，在结构的在线监测中，可将前一时段的测点响应作为基准，计算前后时段动力响应的CVAC值，若明显小于1，则可初步判断结构状态在这一时段有显著变化。

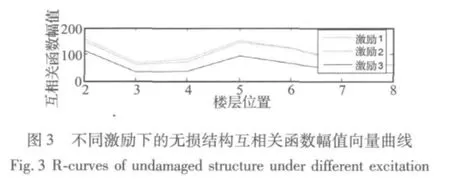
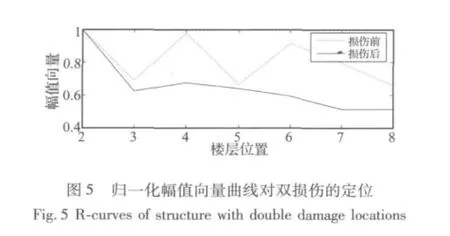
图3中，无损结构在三条不同激励作用下，所有的互相关函数幅值向量曲线形状相似，即曲线形态是固定的，仅会因外激励幅值大小的变化而产生上下平移，若再进行归一化处理，各曲线几乎吻合。这表明用R构造的损伤定位标准具有良好的稳定性和可行性。当框架结构某一层发生损伤时，根据上下相邻传感器所测到的加速度响应时程计算互相关函数，其幅值会产生突变。如图4(a)、图4(b)所示，当第六层框架柱存在损伤时，在互相关函数幅值曲线图上，损伤的定位是很明确的。当四、六层均发生25%损伤时，其归一化处理后的定位曲线如图5，可见幅值向量曲线不仅对单损伤情况下的定位准确，多损伤情况也同样有效。

表1 多种情况下的CVAC值Tab.1 CVAC values of structure

表2 各种损伤情况下的损伤因子K值及误差Tab.2 K values of structure with different damages

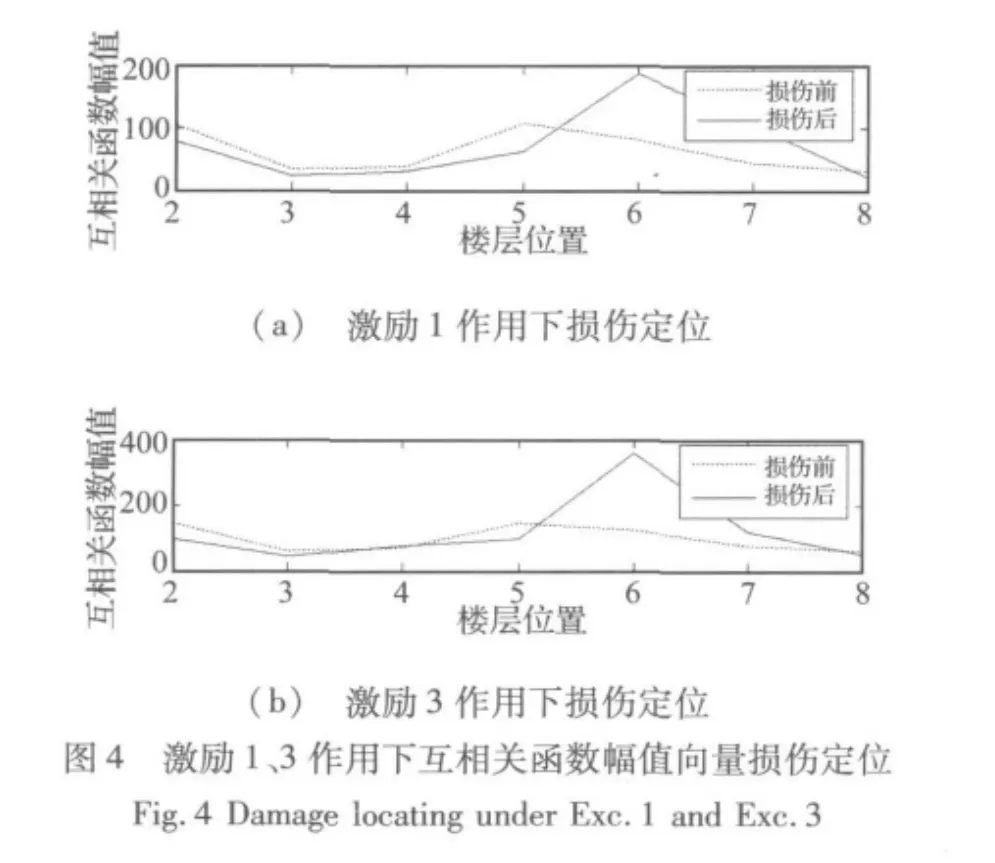
2.3 损伤程度的识别

表2是各种损伤情况下，针对不同激励的采样数据计算得到的损伤因子K值及误差，表中K值均为百分数比值，K1～K5分别表示在第1～5条激励下的计算值。结果表明，单损伤情况下的损伤程度识别的平均精度很高，可达到1%以内。双损伤情况下，误差最大值为5.9%，平均误差在5%以内。构建的损伤因子对损伤程度的量化是有效的。

3 结论

利用土木工程结构在随机激励下的动力响应时程相关函数进行损伤识别的方法是可行的。以八层钢框架结构模型在多条随机激励作用下的试验数据为基础，对相邻测点间的互相关函数幅值向量分别进行曲线定位、损伤因子等分析，结果表明本文提出的方法对损伤的判别、定位及量化是简易、有效的。

若随机激励的频率一定，结构无损时各相邻测点动力响应的互相关函数幅值向量曲线具有相对固定的形态，结构发生损伤后，在损伤处幅值向量曲线会出现突变，利用这一特性可进行损伤定位。试验表明，这一方法对多损伤情况下的定位也同样准确。

参照模态置信度定义的损伤因子CVAC，尽管它与损伤程度之间的量化关系不明确，但对于同一种损伤(或无损)情况下的动测响应，计算值是始终稳定的，这一特性可用于在线监测中结构状态突变的初步判定。

基于互相关函数分析的损伤量化因子K对损伤程度的识别精度良好。

［1］宗周红，任伟新，阮 毅.土木工程结构损伤诊断研究进展［J］.土木工程学报，2003，36(5):105-110.

［2］Ren W X， ZongZ H.Outputonlymodalparameter identification of civil engineering structures［J］.International Journal of Structural Engineering and Mechanics，2004，17(3-4):429-44.

［3］庄表中，陈乃立.随机振动的理论及实例分析［M］.地震出版社，1985.

［4］ JamesIII G H，Came T G，Lauffer J P.The natural excitation technique(NExT)for modal parameter extraction from operating structures［J］.Modal Analysis:The International Journal of Analytical and Experimental Modal Analysis，1995，10(4):260-277.

［5］于哲峰，杨智春.基于互相关函数幅值向量的结构损伤定位方法研究［J］.振动与冲击，2006，25(3):77-80，120.

［6］于哲峰，杨智春.飞机壁板紧固件松脱损伤检测的实验研究［J］.应用力学学报，2008，25(1):99-102.

［7］杨智春，党晓娟，谭光辉.基于互相关函数幅值向量和小波变换的复合材料结构损伤检测［J］.振动与冲击，2008，27(11):17-21.

［8］王 乐，杨智春，王 慧，等.白噪声激励下的复合材料层合结构损伤检测的内积向量法［J］.振动与冲击，2009，28(4):127-131.

［9］Lei J Y，Yao Q F，Lei Y.Damage identification method based on correlation function of structural responses to operational excitation［A］.//Proceedings of international conference on health monitoring of structure，material and environment［C］.Nanjing，2007.