电火花线切割拐角加工切割轨迹的仿真计算与数控轨迹的规划方法

2011-02-10迟关心绕学敏

电加工与模具 2011年2期

迟关心,绕学敏

(哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001)

如何提高电火花线切割中拐角处的加工精度,一直以来都是从事该领域的工作人员所追求的重要指标之一。由于电火花线切割加工过程中挠性电极丝发生弯曲变形,在切割拐角处会造成塌角,以致破坏拐角处的形状精度。目前,数控轨迹控制法是常用的拐角加工精度控制策略之一。在数控代码预定轨迹的基础上,在一些拐角及大曲率位置对实际运行轨迹作实时轨迹偏差补偿,以弥补电极丝变形引起工件形状误差,即基于预测的电极丝变形总量来修正加工拐角和 R角的数控轨迹,提高微细部位的加工精度[1]。Obara,H.[2]等人最近提出一个得到精确的拐角、R角和大弧度凹R角的方法,更引人注意。在这个方法中,在加工拐角和 R角时,对数控轨迹的修正和能量发生器生成能量的控制将同时进行,以使工件中间平面上的拐角加工误差及上平面或下平面的加工误差都减小在允差范围内。

本文对拐角切割时产生的切割轨迹生成方式与过程进行了研究,并对其切割轨迹生成方式进行建模。对该切割轨迹生成方式进行编程并仿真计算,通过与实际加工中获得的数据比较分析后认为,该切割轨迹生成方式的仿真计算结果在一定程度上符合实际加工情况。并且,本文通过该切割轨迹生成方式分析后,提出一种使用较小拐角的直线段作为切割较大拐角的过渡段的直线段轨迹规划方法。最后,对锐角、直角以及钝角分别进行了是否采用数控轨迹规划方法而产生的切割轨迹的对比。

1 拐角加工中切割轨迹生成方式的分析

电火花线切割加工过程中,电极丝会发生振动与弯曲,发生弯曲后的电极丝在水平方向存在一个偏移距离。在加工过程中,Ivano Beltrami利用标准振动方程对电极丝进行数学建模。假设电极丝质量均匀分布,且受轴向张紧力作用;加工过程中,机械力、冲刷力、静电力及电动力垂直作用于电极丝轴向力。在认为电极丝单位长度上作用力是其位置与时间函数的前提下,实现了对在某一弯曲条件下电极丝的建模。实际中,当蚀除参数选择合适时,电极丝不会发生明显的振动。在只考虑电极丝的静态偏移时,对所建立的方程进行简化。并且假设,与工件接触的电极丝部分所受的外部载荷为一个常数值,q(z)=q 0;在丝架两端内除去与工件接触部分的电极丝所受的外部载荷为0,q(z)=0[3]。如图1所示,电极丝的偏移量由D与d两部分组成。

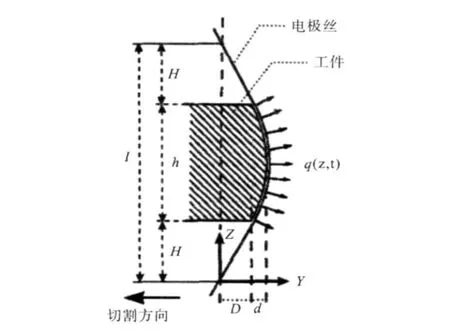
图1 切割中,电极丝形状示意图[1]

对简化后的方程求解偏移量的值:

Ivano Beltrami建立的模型可计算出某瞬时电极丝的偏移量,为后续的数控轨迹修正提供参考。经过研究指导,组成偏移量的两部分中,D段尺寸较大而d段尺寸相对小许多,故在计算中可只考虑D尺寸而忽略d尺寸。从滞后量D的求解可以看出,D值与外部载荷q0呈现出线性关系。在线切割过程中,当电极丝的张紧力保持一定值后,电极丝所受的外部载荷主要是放电作用力(包括放电爆炸力、静电作用力等)。放电作用力与放电能量有紧密的联系。

研究结果表明,在电火花加工过程中,无论正极还是负极,都存在单个脉冲的蚀除量与单个脉冲能量在一定范围内成正比的关系。某一段时间内的总蚀除量约等于这段时间内各个有效脉冲蚀除量的总和,故正、负极的蚀除速度与单个脉冲能量、脉冲频率成正比[4]。用公式表示为:

式中:K为与电极材料、脉冲参数、工作液等有关的工艺系数;W为单个脉冲能量;f为脉冲频率;φ为有效脉冲利用率,它与放电面积成正比关系。

将式(2)除以式(3)得:

在拐角切割中,外载荷 q0与有效脉冲频率、放电面积紧密相关,在此假设q0与有效脉冲频率与放电面积的乘积成正比关系,又因为放电面积与放电角成正比关系,故有q0与放电角θ成正比关系,即q0∝fθ2。同时,假设放电能量 W 与放电面积成正比例关系。由以上假设获得了滞后距离和切割速度之间满足正比例关系,即:

在电火花线切割拐角加工过程中,将引导与滞后轨迹离散化处理后,可认为每一个引导点都有一个与之相对应的滞后点,引导点与滞后点之间的距离即为滞后距离。其中,滞后距离D与切割速度v之间的比值可在直线切割中获得。电极丝切割速度与其运动速度成正比关系。利用以上假设条件得出的切割速度与滞后距离的正比例关系,可进一步对其做仿真计算,并模拟出对应的切割轨迹。

2 拐角加工中切割轨迹的仿真计算

电火花线切割电极丝的运动速度即为滞后点的运动速度,切割轨迹便是滞后轨迹。在滞后距离与切割速度之比为一个常数值的假设下,可计算滞后点在一定时间里的运动距离。并且认为,滞后点由当前时刻位置运动到下一时刻位置的运动方向为当前时刻滞后点的位置指向下一时刻引导点的位置的连线方向。根据以上假设便可对直线与直线组成的拐角在加工过程中的切割轨迹进行仿真计算。

假设线切割加工中,按匀速直线运动时的数控进给速度为 V,进给时间为t,则对应的进给运动距离为 d,电极丝运动距离为 dB,即｜BiBi+1｜(图2);滞后的距离为D。由此可以根据以下公式计算出Bi处的运动距离dB:

图2 数控引导点与滞后点关系

假设引导点在 t时间里的运动距离d= 10;引导点在匀速直线运动时与滞后点之间的滞后距离为H= 100;整个仿真切割过程中,引导点的速率保持不变;拐角的一边与 X轴重合,另一边称为斜边。根据以上条件便可用以下方程进行编程迭代计算,以运算出各点的位置坐标进而连接成为切割轨迹。

利用上述公式对直角进行切割轨迹的仿真运算,并与已获得相关数据进行比较分析(图3和图4)。

图3 直角切割轨迹仿真结果

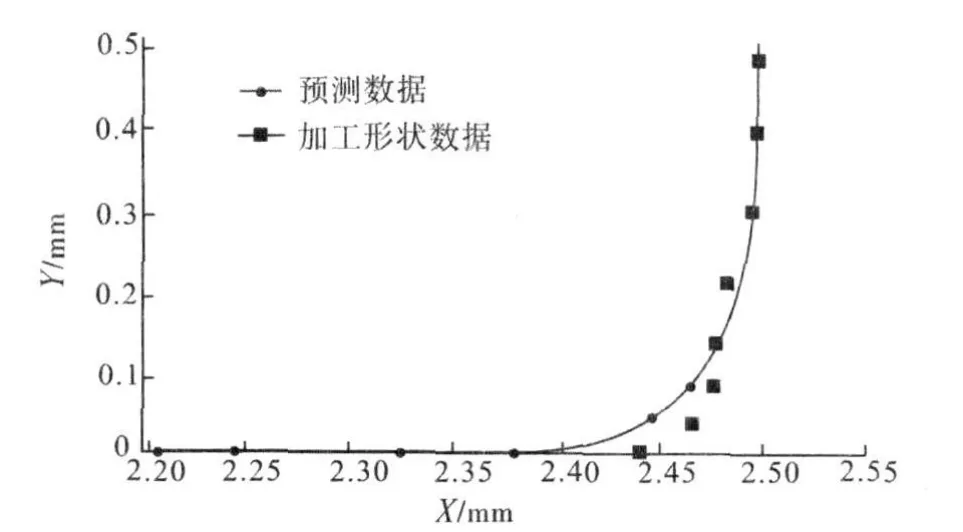
图4 周晓光等人所测量的数据[5]

通过比较图3和图4中的图形及数据,可以说明仿真结果在一定程度上接近实际情况。因此,在一定条件下可利用此切割轨迹的生成方式进行数控轨迹的修正。

图5～图 7给出了 60°、90°、120°角的切割轨迹进行仿真计算的结果。

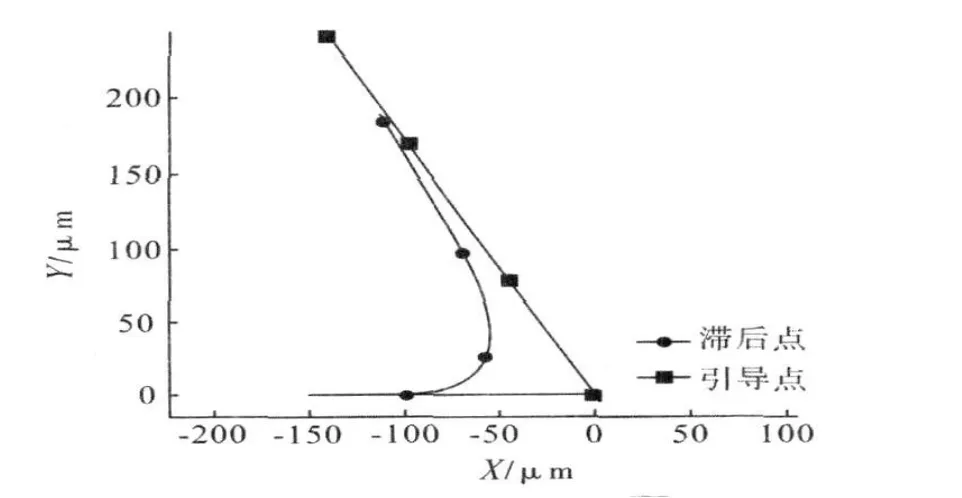
图5 60°锐角切割轨迹仿真

图6 直角切割轨迹仿真

图7 120°钝角切割轨迹仿真

在对锐角、直角与钝角的切割轨迹的仿真计算结果与实际获取的切割轨迹进行比较分析后,可认为该仿真方式能在一定程度上符合实际切割轨迹的生成规律。对大小不同的拐角的切割轨迹分析得知,在引导轨迹的牵引下不断产生滞后轨迹,且在同一时刻下由滞后点指向引导点的向量与 X轴负方向向量两者的夹角由180°不断变小、始终大于当前拐角的大小,最终逼近当前拐角的角度值。同时,由滞后点指向引导点的向量与X轴负方向向量两者的夹角可以计算出。按这两个向量的夹角变化规律分析,可提出用相对较小的拐角引导轨迹作为切割较大拐角的引导过渡段,过渡段结束后再沿较大拐角的斜边轨迹进给。经过引导渡段终点与之对应的滞后点两者连线的斜率应与较大拐角的斜边的斜率几乎一致。与较大拐角斜边的斜率相同并经引导渡段终点的斜线与X轴的交点与过渡拐角的尖点两者间的距离可称作偏移量。不同的过渡拐角条件下,当达到过渡段终点时引导点与滞后点连线的斜率与目标拐角斜边的斜率都几乎一致时,会产生不同的偏移量。偏移量越大,造成的拐角精度误差越小。因此,偏移量可作为一个控制量,以满足实际提出的要求。

3 拐角加工中直线段过渡的引导轨迹规划方式

上一节里提出的用较小拐角的引导直线段作为切割较大拐角引导轨迹的过渡段。此方式的关键之处在于,直线过渡段的终点处滞后点和引导点连线与目标拐角斜边的斜率几乎一致。在确定目标拐角的角度后,偏移量用作对拐角精度误差的一个控制量,同时也决定了过渡拐角的大小、过渡段里各点的坐标数据。

在确定的目标拐角角度下,再给出偏移量的具体范围后,采用如下方式求解出最好的过渡拐角的相关数据。

根据提出的偏移量的范围,求解出符合该条件的所有过渡拐角对应的直线引导轨迹与滞后轨迹的坐标数据、偏移量以及在过渡段终点处引导点与滞后点两者连线的斜率。选择在过渡段终点处引导点与滞后点两者连线的斜率与目标拐角斜边斜率最接近的过渡拐角的相关数据,并返回此过渡拐角对应的偏移量值、引导与滞后轨迹的各点坐标数据。选择斜率最接近的目的是可在由过渡轨迹转接至目标拐角的斜边轨迹时,滞后点能更平滑地过渡到目标斜边轨迹里。根据以上原则,可对具体角度的拐角在一定偏移量范围内作切割轨迹的仿真计算。

假设引导点在单位时间里的运动距离h= 10;引导点在匀速直线运动时与滞后点之间的滞后距离为H= 100;偏移量设置为D= 50;整个仿真切割过程中,引导点的速率保持不变;拐角的一边与X轴重合,另一边称为斜边。根据以上条件便可编程进行迭代计算,以运算出符合要求过渡拐角的相关坐标数据及偏移量。以下分别对60°的锐角、直角以及120°的钝角的切割轨迹进行仿真计算(图8～图10)。

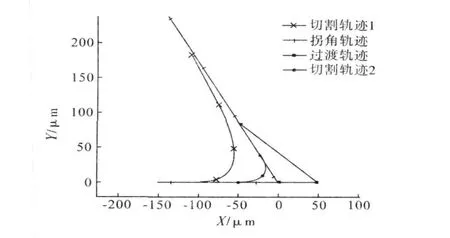
图8 60°锐角切割轨迹对比

图9 直角切割轨迹对比

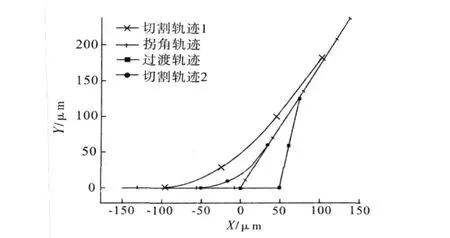
图 10 120°钝角切割轨迹对比

图8～图10中切割轨迹1为未采用直线过渡时切割轨迹的仿真,切割轨迹2为采用直线过渡后切割轨迹的仿真。可见,切割拐角中采用直线段过渡的方式与未采用直线段过渡的方式相比,前者所产生拐角破损面积更小、形状精度更好。可以通过计算拐角的破损面积来衡量采用直线段过渡的切割轨迹所产生的精度误差。通过计算得知,采用轨迹规划后,较没有采用轨迹规划的加工拐角所造成的破损面积小很多。

利用直线段过渡的拐角轨迹规划方式,编写出一个通用的程序,并完成了一个封闭图形的切割模拟仿真,其中包括未引入直线段过渡的规划方式产生的轨迹与引入直线段过渡的规划方式产生的轨迹两者的对比情况。该程序实现了对锐角、钝角与直角角度形状与其方位的识别。在图11中,切割轨迹1为未采用直线过渡时切割轨迹的仿真,切割轨迹2为采用直线过渡后切割轨迹的仿真。