基于GA-BP神经网络的单向走丝线切割机床热误差补偿

陈迪于,芮延年,徐 明,朱 宁

(1.苏州大学,江苏苏州 215021;2.苏州电加工研究所有限公司,江苏苏州 215011)

数控单向走丝线切割机床是一种高精度加工机床,机床的热变形将对其加工精度有较大的影响。据不完全统计:在精密加工中,由机床热变形所引起的制造误差占总制造误差的40%～70%。

目前改善热变形误差的方法主要有3种。一是通过使用新材料来减少材料热变形的膨胀系数,但一旦材料确定后,其热变形的膨胀系数也就确定了;二是通过热态优化设计,即从形状优化和参数优化出发,寻求合理的温度分布和刚度分布,来控制机床结构的热变形,具体操作较困难;三是通过热监测和热补偿技术保证机床的加工精度,这种方法可利用现代监测与智能补偿技术来实现。

本文针对机床加工过程热变形误差模糊不确定性问题,拟通过研究,利用GA-BP神经网络法与热监测和热补偿方法相结合,来减少机床的加工精度误差。

1 GA-BP神经网络误差模型

虽然BP人工神经网络中是一种很好的优化算法,但当系统较为复杂时,存在着学习速度慢;不能很好的保证收敛速度和全局最优点;网络结构不易确定等问题。而GA(遗传算法)采用概率化的寻优方法,能自动获取和指导优化的搜索空间,不需要确定的规则,这样就可利用其优点对BP神经网络进行优化,提高学习速度、保证其收敛的最优性。

1.1 模型构建流程

GA优化BP神经网络算法流程如图1所示。

遗传算法优化BP神经网络分为BP神经网络结构确定、遗传算法优化和BP神经网络预测3个部分。其中,BP神经网络结构确定部分根据拟合函数输入输出参数个数确定BP神经网络结构,进而确定遗传算法个体的长度。遗传算法优化使用遗传算法优化BP神经网络的权值和阈值,种群中的每个个体都包含了一个网络所有权值和阈值,个体通过适应度函数计算个体适应度值,遗传算法通过选择、交叉和变异操作,找到最优适应度值对应个体。BP神经网络预测用遗传算法得到最优个体对网络初始权值和阈值赋值,网络经训练后预测函数输出。

图1 GA-BP神经网络流程图

1.2 BP神经网络部分

(1)确定网络结构

式中:no为输出层节点数;ni为输入层节点数;k为1～10之间的常数;nh为隐含层节点数。

隐含层节点数最终取值没有特别好的办法选择,只能通过多次试算,比较预测结果的方式选择。图2为神经网络的一般结构图。

那么此网络结构就为 ni-nh-no型,网络权值有(ni×nh×nh×no)个,阈值有(nh+no)个。

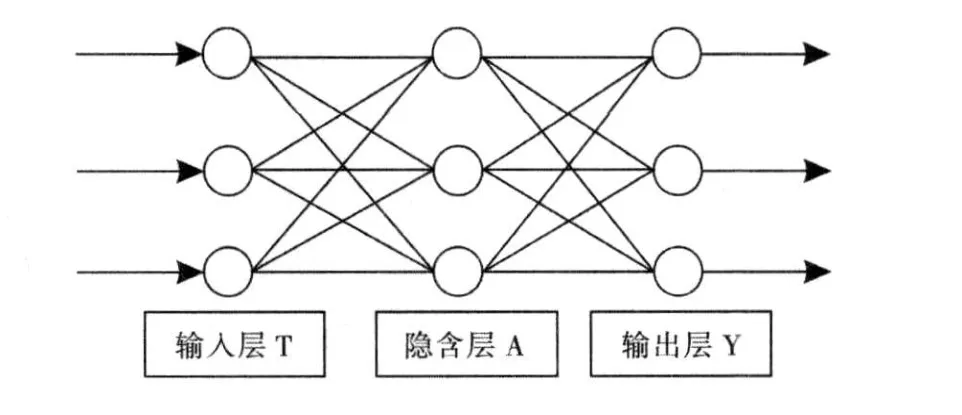
图2 BP神经网络的一般结构

(2)数据预处理

为方便神经网络输入和计算,利用式(2)对其进行归一化预处理,使网络的输入数据介于-1和1之间:

式中:T′为处理后的测点温度;T为原始数据;T max、T min分别为原始数据的最大值、最小值。

对于输出数据(机床热变形量 X=(x1,x2…xno)也采取以上方法进行归一化处理。

1.3 GA算法优化实现

遗传算法的实现涉及到它的5个要素,包括:参数编码、初始群体生成、适应度计算、遗传操作设计和控制参数设定。

(1)参数编码

本文采用的是二进制编码方法,它是遗传算法中最常用的编码方法,使用二值符号集{0,1}进行编码,所构成的个体基因型是一个二进制编码符号串。

(2)初始群体生成

遗传算法是一种对群体进行操作的算法,因此必须为遗传操作准备一个由若干初始解组成的初始群体。初始群体的设定很大程度上依赖于求解问题的性质及编码方案的选择。最常见的是无指导的随机初始化。

(3)适应度函数

根据个体得到BP神经网络的初始权值和阈值,用数据来训练BP神经网络的预测系统,把预测输出和期望输出之间的误差绝对值和作为个体适应度值,计算公式为:

式中:n为网络输出节点数;yi为BP神经网络第i个节点的输出;Oi为第i个节点的预测输出;k为系数。

(4)遗传操作

选择操作;交叉操作;变异操作。详见参考文献[5]。

(5)控制参数选择

在MATLAB编程实现中,控制参数选择是最重要的。遗传算法的参数包括:群体规模 N、编码长度 L、交换概率Pc、变异概率Pm等。控制参数的选择非常关键,控制参数的不同选取会对遗传算法的性能产生较大的影响,详见文献[5]。

按照此GA算法的寻优计算方法,不断优化BP网络的权值和阈值,直到适应度函数值最小为止,此时的BP神经网络即为该数据组的最优预测模型。然后根据优化的BP神经网络去预测机床的热变形误差值。根据实验分析其预测残差。

2 实验研究

2.1 机床热变形测试实验

本测试实验对象是DK 7632型低速走丝线切割机床,同时监测机床上的测点温度和对应的热变形量。在静态下,模拟数控单向走丝线切割机床加工过程的发热情况,每隔15 min电脑自动采集一次测点温度和热变形位移量:

式中:c为记录次数;Tc1…Tc10为经专家经验初选的10个温度点在第 c次测得的温度;xc,yc,Axc,Ayc,zc分别为第c次测得的热变形X,Y轴方向的线位移和角位移及Z轴方向的线位移。

通过对机床的调试,把第一次记录的热变形量作为参照记为0,即:x1=0,y1=0,Ax1=0,Ay1=0,z1=0。

2.2 确定GA-BP模型结构

根据实验简介,结合模糊聚类法将温度测点优化成5个主要测点,据此来预测热变形量。那么,其输入输出节点数就都是5个,隐含层经多次试算去7个。此网络结构就为5-7-5型,网络权值有70个,阈值有7+5=12(个)。此时网络结构即为图3所示,其对应优化后的网络权值和阈值见表1。

图3 BP神经网络结构

表1 BP神经网络最优权值和阈值表

根据上述原理选定如下主要控制参数值:

3 实验研究

3.1 实验简介

(1)实验设备

数控单向走丝线切割机床,温度传感器,位移传感器,USB数据采集卡,笔记本电脑等。建立的实验平台如图4所示。

图4 实验平台

(2)实验目的

优化数控单向走丝线切割机床的温度测点,建立优化后的测点温度变化和机床热变形量的数学关系模型。根据不同的建模方法,对比各模型的有效性。

(3)实验方法

按照专家经验初选出10个温度点,安上温度传感器,记各点温度为 T=[T1,T2,…T10]。

3.2 热误差的预测分析

为了体现GA-BP神经网络模型对此种机床的热变形误差预测能力,将传统的BP神经网络预测模型与之对比。利用以上GA-BP网络模型进行预测,并绘出预测结果与实际测量结果的残差图(图5a)。图5b是BP神经网络预测残差图。

从图5a可看出:GA-BP网络的预测残差的绝对值之和为46. 5;而BP网络的预测残差的决定值之和为54.95。

比较图5a与图5b,可以看出用经过GA优化的BP神经网络法来预测,要比BP神经网络来预测的效果好,而且相对来说数据都较集中,因此用GABP神经网络法预测单向走丝数控线切割机床的热变形误差是非常有效的。

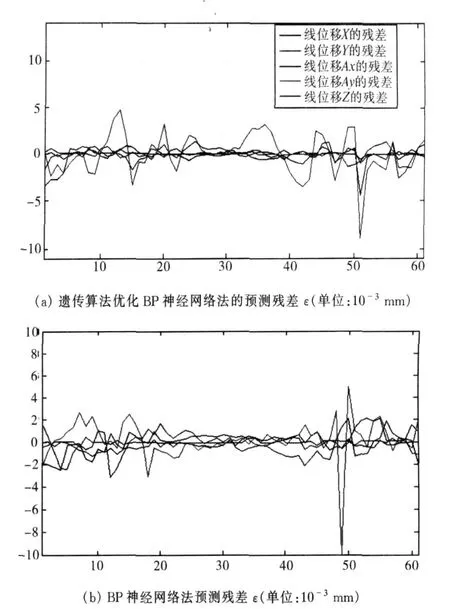
图5 预测残差

4 结束语

机床热误差补偿问题的难点和关键点就是建立热误差预测模型。本文在GA-BP神经网络建模方法下,预测低速走丝线切割机床热变形误差。经实验结果分析表明,所建模型能正确反映此种机床的热误差变化规律,且预测精度高于传统BP神经网络预测模型,预测残差较平缓集中、峰值较小,因此用此GA-BP神经网络法建立的机床热误差预测模型,可以用于此机床的热误差补偿中,将能有效提高机床热误差补偿的精度。

[1]郭前建,杨建国.基于蚁群算法的机床热误差建模技术[J].上海交通大学学报,2009(5):803-806

[2]杨建国,张宏韬,童恒超等.数控机床热误差实时补偿应用[J].上海交通大学学报,2005,39(9):1389-1392.

[3]曹岩等.MATLAB数学和控制教程[M].北京:化学化工出版社,2009.

[4]张德丰等.MATALB神经网络应用设计[M].北京:机械工业出版社,2009.

[5]韩瑞锋编著.遗传算法原理与应用实例[M].北京:兵器工业出版社,2010.