低信噪比下长码直扩信号的符号宽度估计
2011-02-10牟青,魏平
牟 青,魏 平
(电子科技大学电子工程学院 成都 611731)
直接序列扩频(DS-SS)信号的检测和盲估计是通信信号侦察的重要研究内容。就非合作接收机而言,未知扩频码使得接收无法直接获得扩频增益,因而在低信噪比下对它的截获变得更加困难。假定没有任何扩频码生成机制的先验知识,为了估计扩频码,通常需要先估计出伪码周期,然后利用周期积累估计出扩频码。到目前为止,相关研究大都针对的是短码直扩信号[1-5],即伪码周期恰好等于信息码宽。与短码直扩信号相比,长码直扩信号的形式要复杂得多,对其截获也要困难得多。从非合作接收的角度,长码直扩信号分为两类,一类是伪码周期非常长,无法接收到完整的单个伪码周期的信号,对该类长码信号的截获,需要对伪码生成机制有一定的了解;另一类是伪码周期长于信息码码宽的信号,对该类长码信号的截获不需要伪码生成机制的先验知识,以及对该类长码直扩信号有一定的研究[6-11],本文研究也将针对该类长码直扩信号。
在短码直扩信号中,符号宽度与伪码周期长度相等而不需单独估计。与短码直扩信号相比,长码直扩信号首先要面临符号宽度估计的新问题。尽管伪码估计和盲解扩都需要符号码宽参数[6-8],对符号码宽(或符号速率)的估计却很少见到公开的研究结果[11]。文献[11]提出了一种基于相关函数波动的符号码宽估计方法,该方法沿袭了文献[2]所提出的伪码周期估计方法的思想。实际上,伪码周期与符号码宽在本质上是有所不同的:由于伪码序列未知,因此伪码周期是一个完全未知波形的周期;而符号序列每个符号的波形均是已知门函数,且符号序列并非周期序列。文献[11]所提出的符号码宽估计方法是基于直观观察,即相关函数以符号码宽为周期波动,而没有理论推导。事实上可以验证,该现象只发生在以m序列为伪码的直扩信号的情况下,此外,作为符号码宽估计,该性能也并不理想。
本文提出了一种基于差分伪码解扩的方法,由于该方法考虑到了符号码的特殊结构,因而提供了更好的估计性能。
1 信号模型
为了简便,假定接收到的长码直扩信号为BPSK调制,且已经过解调且采样速率恰好为码元速率,则接收机端基带直扩信号可表示为:


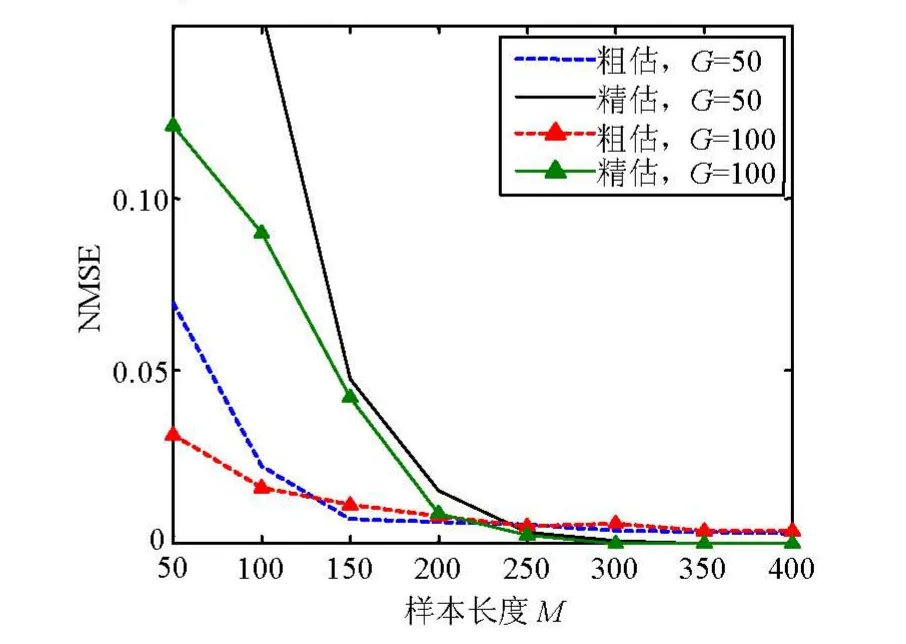
本文假定伪码周期整数L已知,需要估计G,且1 和经典参数估计问题不同,符号码宽估计是一种特殊的参数估计问题。对于经典的参数估计,信号的模型是确定的,待求参数理论上均可通过极大似然(ML)函数求解,但是符号码宽的不同取值对应了不同的信号模型,因此极大似然解不一定能得到满意的结果。考虑到未知参数众多,流行的模型估计方法如最大描述长度(MDL)和贝叶斯信息准则(AIC)[12]不方便用于该问题。本文首先采用对模型变化不太敏感的方法粗略估计符号码宽,然后在较小的模型变化范围内按照参数估计的方法精确估计符号码宽。 由于粗略估计时完全消除了信号中的伪码周期特征,因此估计不受伪码周期干扰,具有鲁棒性。 尽管粗略估计简单直接,可靠的粗略估计对正确估计符号码宽至关重要,但由于它在构造序列组时只利用了部分结构特征,因而提供的精度是不够的。差分伪码解扩将解扩和基于循环自相关函数估计码元速率(cyclic correlation-based symbol-rate estimator,CCS)算法[13]结合在一起。 检测峰值,并选取距零频最近的峰值作为码元速率1/G的估计。CCS法估计码元速率最大的优点是计算简单、易操作。为了把CCS用于DS-SS信号的符号码元速率估计,首先简要分析CCS的估计原理。 利用计算机仿真实验评估提出的符号宽度估计本文方法的性能。在仿真中,每个点分别独立进行100次试验。采用归一化均方误差(NMSE)评估符号码宽估计的性能: 图1和图2考察了在不同信噪比下符号码宽估计算法在伪码为m序列和Gold序列时的性能。图1为本文提出的方法,图2为文献[11]提出的方法。其中,伪码长度L=127,G=100,M=200。 图1 本文方法在不同伪码下的估计性能 在图2中,当伪码为Gold码时几乎失效,因为文献[11]利用的相关函数的周期波动现象只在伪码为m序列时才会存在。比较图1和图2可以看到,当伪码为m序列时,本文方法的性能仍好于文献[11]所提出的方法,可以在低信噪比下进行估计。 图2 文献[11]的方法在不同伪码下的估计性能 图3显示了不同样本长度下,本文提出方法的性能与符号码宽长度的关系。由于该方法与伪码无关,每次实验中伪码按照独立同分布±1等概率取值的随机序列产生,其长度L=127。由图3可以看到,NMSE随着样本长度的增加而减小。当样本长度较小时,粗略估计的NMSE要低于精确估计值;反之亦然。因为在样本长度较小时,由于噪声影响,差分伪码序列估计是不可靠的,因此粗略估计值误差很大;相反粗略估计只利用了高阶自相关函数,噪声对它的影响要小一点。综合图1和图3,一方面粗略估计在低信噪比和短样本长度下的表现好于精确估计,因此是一种鲁棒的方法。另一方面,符号码宽G=100时,估计的NMSE略小于符号码宽G=50时。因为较小的G意味着较低的扩频增益,从而降低了符号码宽估计的性能。 图3 本文提出的方法在不同符号宽度下的性能 长码直扩信号的符号码宽估计对于长码直扩信号截获非常重要,但获得的理论关注较少。本文提出了一种新的估计方法,首先构造高阶自相关函数进行粗略估计;然后利用差分解扩和循环自相关函数进行精确估计,在低信噪比下获得了较好的性能。推导和仿真也表明,该方法性能与扩频码无关,适合非合作场景使用。 [1] TSATSANIS M K, GIANNAKIS G B. Blind estimation of direct sequence spread spectrum signals in multipath[J].IEEE Trans Signal Process, 1997, 45(5): 1241-1252. [2] BUREL G. Detection of spread spectrum transmissions using fluctuations of correlation estimators[C]//ISPACS’2000, IEEE Int Symp on Intelligent Signal Processing and Communication Systems. Kitami: Kitami Institute of Technology, 2000. [3] BOUDER C, AZOU S, BUREL G. Performance analysis of a spreading sequence estimator for spread spectrum transmissions[J]. J Franklin Inst, 2004, 341(7): 595-614. [4] ZHAN Y, CAO Z, LU J. Spread spectrum sequence estimation for DSSS signal in Non-cooperative communication systems[J]. IEE Proc Commun, 2005,152(4): 476-480. [5] 张花国, 李立萍, 陈天麒. 一种DS/SS信号盲同步算法[J].电子科技大学学报, 2007, 36(2): 207-209. ZHANG Hua-guo, LI Li-ping, CHEN Tian-qi. An approach to blind synchronization of DS/SS signals[J]. Journal of University of Electronic Science and Technology of China,2007, 36(2): 207-209. [6] AGEE B G, KLEINMAN R J, REED J H. Soft synchronization of direct sequence spread spectrum signals[J]. IEEE Trans Comm, 1996, 44(11): 1527-1536. [7] QUI P Y, HUANG Z T, JIANG W L, et al. Improved blind-spreading sequence estimation algorithm for direct sequence spread spectrum signals[J]. IET Signal Process,2008, 2(2): 139-146. [8] 张天骐, 周正中, 林孝康, 等. 低信噪比长伪码直扩信号的盲估计方法[J]. 信号处理, 2008, 24(6): 370-376. ZHANG Tian-qi, ZHOU Zheng-zhong, LIN Xiao-kang, et al.Appraoch to blind estimation of lower SNR long code DS signals[J]. Signal Processing, 2008, 24(6): 370-376. [9] 张天骐, 周正中, 邝育军, 等. 低信噪比长伪码直扩信号伪码周期的估计方法[J]. 系统工程与电子技术, 2007,29(1): 12-16. ZHANG Tian-qi, ZHOU Zheng-zhong, KUANG Yu-jun, et al. New method for periodic estimation of the PN sequence in the lower SNR long code DS-SS signals[J]. Systems Engineering and Electronics, 2007, 29(1): 12-16. [10]王满喜, 李宏, 马刈非, 等. 低信噪比下非周期性直扩信号的盲估计[J]. 电子科技大学学报, 2009, 38(2): 177-181. WANG Man-xi, LI Hong, MA Yi-fei, et al. Blind estimation of lower SNR aperiodic DS signals[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(2): 177-181. [11] 徐海源, 王丰华, 黄知涛, 等. 低信噪比下非周期性直扩信号的盲估计[J]. 国防科技大学学报, 2007, 29(6): 44-48. XU Hai-yuan, WANG Feng-hua, HUANG Zhi-tao, et al.Blind estimation of the symbol rate of a long code DSSS signal[J]. Journal of National University of Defense Technology, 2007, 29(6): 44-48. [12] SEGHOUANE A K. Asymptotic bootstrap corrections of AIC for linear regression models[J]. Signal Processing,2010, 90(1): 217-224. [13] CIBLAT P, LOUBATON P, SERPEDIN E, et al.Asymptotic analysis of blind cyclic correlation-based symbol-rate estimators[J]. IEEE Trans Inform Theory,2002, 48(7): 1922-1934. 编 辑 税 红2 基于差分伪码解扩的符号码宽估计
2.1 符号码宽的粗略估计计

2.2 符号码宽的精确估计计




2.3 本文提出算法总结

3 仿真试验



4 结 论
