基于EEMD穿墙雷达人的运动模式识别

王 宏，周正欧，李廷军，孔令讲

(电子科技大学电子工程学院 成都 610054)

对穿墙雷达的研究主要分为成像[1-3]和动目标多普勒探测两大类[4-6]。由于人的心跳、呼吸、手臂摆动、行走、跑步等运动的多普勒信号属于非线性、非平稳信号，具有丰富的多普勒频移分量，因此对人的运动多普勒特性分析已成为穿墙雷达研究的一个热点。文献[4]采用多普勒和阵列处理相结合的方法，不仅能够确定多个动目标的多普勒频移，而且能够同时分辨多个动目标的方位。文献[5]采用短时傅里叶变换(STFT)对人在自由空间中的7种运动模式进行时频分析，根据时频特征提取6种参数作为特征向量，并采用支持向量机学习算法进行了分类。但在穿墙探测情况下，由于测量的多普勒信号信噪比低，信号的许多微多普勒特征被噪声掩盖，从而无法提取相应的特征向量用于分类。文献[6]利用EMD对人的运动多普勒特性进行分析，通过对STFT和EMD两种方法的时频分布比较，表明EMD具有更高的多普勒时频分辨力，更能反映信号时频分布的细节特征。文献[7]提出了一种新的自适应信号处理方法，根据信号的局部极值特征将原信号分解为一系列的本征模式函数(IMF)，每个IMF体现了蕴含在原信号中不同频率尺度的振荡特性，适用于非线性、非平稳信号。然而EMD方法存在模式混合问题，造成信号时频分布的偏移，使得每个IMF的物理意义不明确。为了解决该问题，在对白噪声特性进行EMD分析的基础上[8]，一种改进的EMD方法——整体平均经验模式分解(EEMD)方法被提出[9]，能够自动消除EMD分解存在的模式混合问题。

本文利用穿墙雷达对墙后人的静止站立(测量呼吸和心跳)、站立摆动手臂、前进又后退一步、行走和跑步5种运动进行多普勒测量，分别采用EMD和EEMD将人的各种运动的多普勒信号分解为一系列IMF；采用支持向量机学习算法，将分解后的各IMF能量占总能量的百分比作为特征向量用于训练和识别；比较了EMD和EEMD的识别率，分析了特征向量维数选取对识别率的影响。

1 穿墙雷达多普勒测量

穿墙雷达进行多普勒探测的实验原理如图1所示。压控振荡器VCO产生的750 MHz单频连续波信号通过功分器后，一路经发射天线辐射出去，另一路与经过低噪放大后的含有多普勒频移信息的接收信号进行混频，将混频后的信号进行低通滤波，获得多普勒频移信号。使用Agilent DSO80804B数字示波器进行采样，采样率为50 kHz/s，每次测量都连续采样20 s。图2为实测场景，穿墙雷达位于一间教室的走廊上，收发天线采用对数周期天线，紧贴墙壁放置，墙厚15 cm。对教室内人的5种运动分别进行多普勒测量，每种运动的具体描述如表1所示。分别对5个人进行了测量，每人每种运动测量多次，共采集样本564组。

图1 穿墙雷达多普勒测量原理框图

图2 穿墙雷达多普勒实测场景

表1 人的5种运动分类及其描述

2 经验模式分解

2.1 EMD

EMD是一种基于信号局部极值特征的自适应信号分析方法，它将任一信号x(t)分解成一系列的IMF，每个IMF满足两个条件：1) 信号极值的数目和零点的数目必须相等或最多相差一个；2) 在任意一点处，极大值包络和极小值包络的平均值为零[7]。EMD分解的具体步骤如下：

1) 分别找出信号序列的所有极大值点和极小值点，采用三次样条函数拟合成该序列的上、下包络线，上、下包络线的均值为该序列的平均包络线m1(t)。

2) 将信号x(t)减去平均包络线m1(t)，得到一个去掉低频的新序列h1(t)，即：

通常，h1(t)不是一个平稳信号序列，所以再将h1(t)作为待处理的信号x(t)重复步骤1)和步骤2)，直到满足判定条件SD表示连续两次迭代结果的标准偏差，取值区间一般为[0.2, 0.3]。得到第一个IMF分量C1(t)= h1k(t)，k表示达到判定条件时的迭代次数。

3) 减去C1(t)，得到一个去掉高频成分的差值信号序列r1(t)：

4) 对r1(t)进行上述平稳化处理过程，得到第2个IMF分量C2(t)，如此重复，直到最后一个差值序列rn(t)为单调函数，不可再被分解为止。此时，残余量rn(t)代表原始信号序列的均值或趋势。原始信号序列即可由这些IMF分量以及残余项rn(t)表示，即：

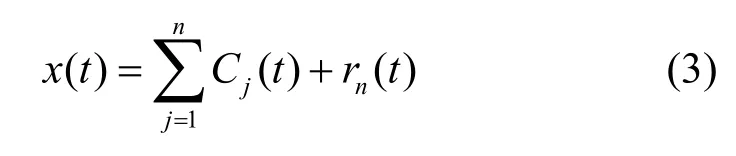
2.2 EEMD

为了解决EMD分解存在的模式混合问题，EEMD方法被提出[9]。EEMD是一种借助于噪声的数据分析方法，每次将不同的白噪声人为添加到原始信号中，并对添加了白噪声的信号进行EMD分解，共进行若干次，将所有分解获得的相应IMF求平均，得到最终的IMF，作为原始信号的基函数。

EEMD算法步骤如下：

1) 将一定强度的白噪声加到信号上。

2) 将添加了白噪声的信号进行EMD分解，得到各IMF分量。

3) 重复执行步骤1)和步骤2)，共进行M次，每次添加不同的白噪声序列。

4) 对M次EMD分解得到的相应IMF求整体平均，将其作为原始信号的最终IMF，即：

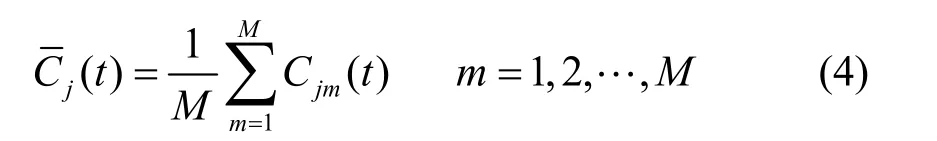
EEMD消除模式混合的本质在于：对于每次EMD分解，添加的白噪声在整个时频空间是均匀分布的，而信号的不同频率尺度被自动投影到由白噪声所建立的均匀时频空间的相应频率尺度上。由于每次EMD分解添加的白噪声不同，噪声之间不相关，因此，对所有EMD分解的相应IMF求整体平均后，人为添加的噪声被抵消。本文对所有实验采集的多普勒信号进行EEMD分解时，添加的白噪声幅度均为原信号标准差的0.2倍，整体平均次数M=50，再增加对分解结果改善不大。

图3给出了人前进又后退一步时EMD分解的IMF6、IMF7及其频谱。图4为相应运动的EEMD分解的IMF6、IMF7及其频谱。比较图3和图4，可以看出EEMD分解得到的IMF6和IMF7对应的频率范围分别是10～20 Hz(图4(b))和1～5 Hz(图4(d))，而EMD分解的IMF6的频谱分布(图3(b))既覆盖了EEMD中IMF6的频率范围10～20 Hz，也覆盖了IMF7的频率范围1～5 Hz。所以EMD分解的IMF6出现了模式混合问题，但是在EEMD分解中得到了很好的抑制。同样，对其他几种运动的分析也会得到相似的结论。因此EEMD能够消除模式混合问题，IMF的物理意义更明确，每个IMF能够正确反映信号在不同频率范围内的振荡特性。

图5给出了人的5种运动经EEMD分解后的HHT谱。可以看出不同运动的时频特征各不相同，多普勒频移大小与人的运动速度和发射信号的频率有关，目标径向运动速度越大，发射信号频率越高，多普勒频移越大。本文测量时的发射信号频率为750 MHz，总体上多普勒频移范围较低，基本在12 Hz以下。

图5a显示人静止站立时呼吸和心跳的多普勒频率最低，主要分布在2 Hz以下，其他均为噪声；图5d中人行走的多普勒频率既包括躯干移动的多普勒频率，也包括手臂摆动的多普勒频率，由于行走中躯干移动速度慢，其多普勒频率较低；图5e中，由于人跑步时手臂的摆动速度快，产生的多普勒频率在5种运动中最大，频移范围最宽。站立摆动手臂和前进又后退一步相对行走和跑步而言运动模式更单一，因此该两种运动时频图上的周期性变化更清晰，如图5b和图5c所示。

图3 人前进后退一步EMD分解的IMF6、IMF7

图4 人前进后退一步EEMD分解的IMF6、IMF7

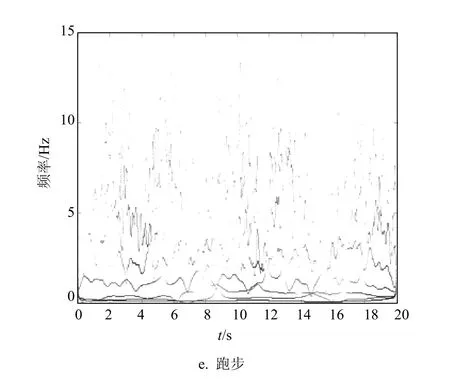
图5 5种运动EEMD分解的HHT谱

3 支持向量机特征向量提取及识别

支持向量机是一种新型机器学习算法，它根据文献[10]的结构风险最小化原则构造学习机器，在使训练错误最小化的同时尽量提高学习机的泛化能力。支持向量机分类的基本原理是寻找一个满足分类要求的最优超平面，在保证分类精度的同时，能够使超平面两侧的间隔最大化。由于支持向量机学习算法是一个凸二次规划问题，所求得的解是全局最优解，优于其他基于经验风险最小化原则的学习算法(如神经网络学习算法等)，故被广泛用于模式识别、回归预测等领域。目前支持向量机已由最初的两类分类器推广为多类分类器[11-12]，本文将其用于人的多种运动的模式识别。

采用支持向量机进行分类，最关键的是特征向量的选取。特征向量数目太少，反映的运动特征信息不足，则分类的准确性就会降低；特征向量数目太多，某些特征向量对提高分类的正确率基本没有贡献，会过多地浪费训练和识别时间。因此，恰当选取特征向量不仅能够提高模式识别的速度，而且能够充分保证识别的正确率。

图6给出了5种典型运动经EEMD分解后各IMF的能量百分比。每种运动以及背景噪声经EEMD共分解为14个IMF。可以看出，背景噪声的各IMF能量随着频率由高到低呈现指数下降趋势。静止站立，由于人的心跳和呼吸的多普勒信号频率很低且非常微弱，因此曲线中代表噪声的高频能量的占比大；而IMF11～IMF13的能量占比相对背景噪声而言有所提高，代表心跳和呼吸。对于后面4种运动，由于穿墙雷达的发射功率较大，测量的多普勒信号经过低通滤波器后大部分噪声被滤除，因此相比静止站立，前面几个代表噪声的IMF的能量占比很小。站立摆动手臂的多普勒频移主要集中在IMF8～IMF13，其中IMF9和IMF10的能量较大。前进后退一步的多普勒频移也主要集中在IMF8～IMF13，但与手臂摆动相比，能量在IMF8～IMF11的频带范围内分布较均匀。对于行走和跑步，由于躯干运动的多普勒频移低、反射强，因此在IMF12处两种运动均出现了一个能量峰值。另外，由于跑步时手臂的摆动频率高于行走时的摆动频率，因此在跑步中代表手臂摆动的IMF6和IMF7的能量占比相对较高，而在行走中代表手臂摆动的IMF9和IMF10的能量占比高。从图6可以看出，不同运动的各IMF能量占比及顺序能够充分反映不同运动的多普勒频移特征，且差异较大，因此适合作为支持向量机的特征向量。

实验中采集的5种运动的总样本数为564组，每组数据分别采用EMD和EEMD分解，依次选取部分或全部IMF的能量占比作为特征向量，组成相应的样本集，将样本集的2/3作为训练，余下的1/3作为识别。图7是支持向量机分类正确率与特征向量维数(即选取的IMF的个数)之间的关系曲线。由于每种运动的多普勒频移主要集中在低频段，因此特征向量的维数是从最后一个IMF开始向前选取若干个IMF来计算的。由于全部14个IMF才能充分反映每种运动的多普勒频移信号特征，因此其分类正确率高于采用部分IMF作为特征向量的情况。另外，从图7还可以看出，EEMD的分类正确率要明显高于EMD，原因在于采用EEMD分解能够消除EMD分解中存在的模式混合问题，使得每个IMF均能够正确反映不同运动多普勒信号在相应频率范围内的振荡特性。采用EEMD分解的最大分类正确率为94.68%，远高于EMD分解的76.19%。

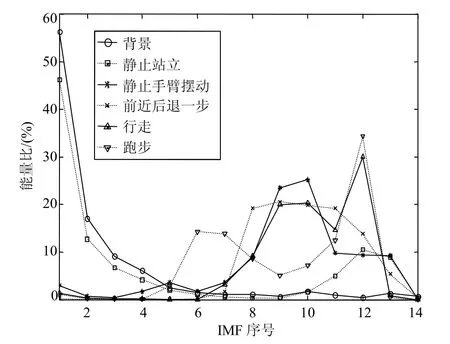
图6 人的5种运动各IMF能量百分比

图7 分类正确率与IMF个数间的关系

4 结束语

分别采用EMD和EEMD对穿墙雷达多普勒探测中人的静止站立、站立摆动手臂、前进又后退一步、行走、跑步共5种运动的多普勒信号进行分解，将两种分解获得的IMF作比较，得出采用EEMD能够消除EMD分解存在模式混合问题的结论。

提取各IMF能量占总IMF能量的百分比作为特征向量，对实验采集的564组数据采用支持向量机学习算法进行模式识别。通过分析特征向量维数对识别率的影响，以及比较EMD和EEMD两者的识别率，表明以EEMD分解后的全体IMF为特征向量的支持向量机的识别率最高，可达到94%以上。

[1] AHMAD F, AM IN M G, KASSAM S A. Synthetic aperture beam former for imaging through a dielectric wall[J]. IEEE Trans Aerosp Electron Syst, 2005, 41(1): 271-283.

[2] KONSTANTIN M Y, ENGHETA N, HOORFAR A, et al.Adaptive polarization contrast techniques for through-wall microwave imaging applications[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(5): 1362-1374.

[3] DOGARU T, LE C. SAR images of rooms and buildings based on FDTD computer models[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(5): 1388-1401.

[4] RAM S S, LING H. Through-wall tracking of human movers using joint Doppler and array processing[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(3):537-541.

[5] KIM Y, LING H. Human activity classification based on micro-Doppler signatures using a support vector machine[J].IEEE Trans on Geoscience and Remote Sensing, 2009, 47(5):1328-1337.

[6] LAI C P, NARAYANAN R M, RUAN Q, et al.Hilbert-Huang transform (HHT) analysis of human activities using through-wall noise and noise-like radar[J] IET Radar,Sonar, and Navigation, 2008, 2(4): 244-255.

[7] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc Roy Soc London, 1998, 454A: 903-995.

[8] WU Z H, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proc Roy Soc London, 2004, 460A: 1597–1611.

[9] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2008, 1(1): 1-41.

[10] VAPNIK V N. Statistical learning theory[M]. New York:Wiley, 1998.

[11] CHEONG S, OH S H, LEE S Y. Support vector machines w ith binary tree architecture for multi-class classification[J]. Neural Information Processing, 2004, 2(3): 47-51.

[12] HSU C, LIN C. A comparison of methods for multiclass support vector machine[J]. IEEE Trans Neural Netw, 2002,13(2): 415-425.

编 辑 税 红